Hint: Differentiate between Empirical probability and theoretical probability in order to find the two for a variety of cases.
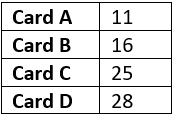
Question.1. Tanvi has a box containing four cards labelled A, B, C and D. She randomly picks a card from the box, records the label on the card and put it back in the box. She repeats this experiment 80 times and records her observation in the table shown below.
Which of the following shows the empirical probability and theoretical probability of picking Card C the next time?
(a) Empirical probability = \frac{5}{16}; Theoritical probability = \frac{1}{4}
(b) Empirical probability = \frac{5}{16}; Theoritical probability = \frac{1}{2}
(c) Empirical probability = \frac{5}{11}; Theoritical probability = \frac{1}{4}
(d) Empirical probability = \frac{5}{11}; Theoritical probability = \frac{1}{2}
Question.2. Mandy has a bag containing 1 red, 1 green, 1 yellow, 1 black and 1 blue ball. She randomly picks the ball from the bag notes it colour and keeps it back in the bag. She repeats this 40 times. The table shows the number of times each colour ball she gets. The number of times the black ball is picked is missing in the table.
She then repeats the experiment 10 more times and gets red ball twice, green ball once, yellow ball thrice, black ball once and blue ball thrice.
Which of these is a valid conclusion as the number of trials of the experiment increases?
(a) The empirical probability of picking yellow ball gets closer to its theoretical probability.
(b) The empirical probability of picking red ball does not get closer to its theoretical probability.
(c) The empirical probability of picking yellow ball gets further away from its theoretical probability.
(d) The empirical probability of picking red ball becomes equal to its theoretical probability.
Ans.1. (a) Empirical probability = \frac{5}{16}; Theoritical probability = \frac{1}{4}
Ans.2. (a) The empirical probability of picking yellow ball gets closer to its theoretical probability.
Hint: Calculate the probability of given events in an experiment in order to comment whether they are complementary events / Sure event / impossible event.
Question.3. If a card is drawn from a deck of cards, what is the probability of a card drawn to be a red or a black card and what can we say about that event?
(a) 1 and it is a sure event.
(b) 0 and it is a sure event.
(c) 1 and it is an impossible event.
(d) 0 and it is an impossible event.
Question.4. A spinner is shown below. 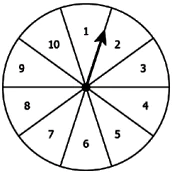
Event A: The spinner lands on a multiple of 11.
Event B: The spinner lands on a number less than 11.
Event C: The spinner lands on a number more than 10.
Which of the following statement is true about the three events?
(a) Probability of Event A is 1, so A is a sure event while the probabilities of Events B and C are 0, so they are impossible events.
(b) Probability of Event A is 1, so A is an impossible event while the probabilities of Events B and C are 0, so they are sure events.
(c) Probability of Event B is 1, so B is a sure event while the probabilities of Events A and C are 0, so they are impossible events.
(d) Probability of Event B is 1, so B is an impossible event while the probabilities of Events A and C are 0, so they are sure events.
Ans.3. (a) 1 and it is a sure event.
Ans.4. (c) Probability of Event B is 1, so B is a sure event while the probabilities of Events A and C are 0, so they are impossible events.
Hint: Represent using organized lists, tables, or tree diagrams in order to List the sample space for compound events.
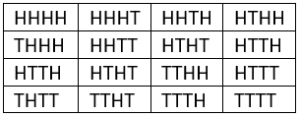
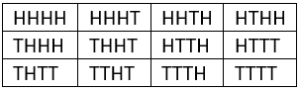
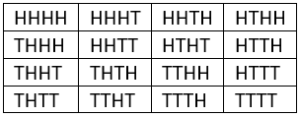
Question.5.When four coins are tossed simultaneously, which of the following represents the sample space?
(a) 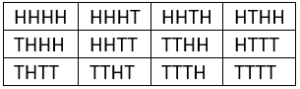
Question.6. To win a price in a game, you need to first choose one of the 4 doors, 1, 2, 3, 4 and then need to choose one of the three boxes A, B, C and then need to choose between two colours red and green.
How many of the possible outcomes of this game include selecting Box A and red colour?
(a) 4
(b) 8
(c) 12
(d) 24
Ans.5. (c) 
Hint: Calculate the probability of various events in order to rank them from most to least probable.
Question.7. A box has 10 equal size cards. Of the 10 cards, 4 are blue, 3 are green, 2 are yellow and 1 is red. If a card is randomly drawn from the box, which is the colour that the card is most likely to have?
(a) Red
(b) Blue
(c) Green
(d) Yellow
Question.8. Of 50 students in a class, 16 prefer cricket, 8 prefer football, 7 prefer basketball and rest of the students prefer either tennis or hockey. There are twice as many students who prefer tennis as the number of students who prefer hockey. A student is randomly selected from the class. Which statement is correct?
(a) The probability of selecting a student who prefer tennis is more than that of selecting a student who prefer cricket.
(b) The probability of selecting a student who prefer hockey is more than that of selecting a student who prefer cricket.
(c) The probability of selecting a student who prefer hockey is more than that of selecting a student who prefer tennis.
(d) The probability of selecting a student who prefer basketball is more than that of selecting a student who prefer cricket.
Ans.7. (b) Blue
Ans.8. (a) The probability of selecting a student who prefer tennis is more than that of selecting a student who prefer cricket.