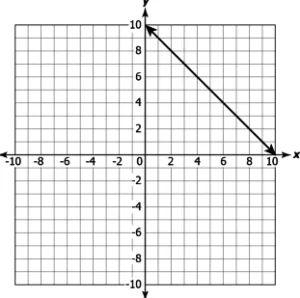
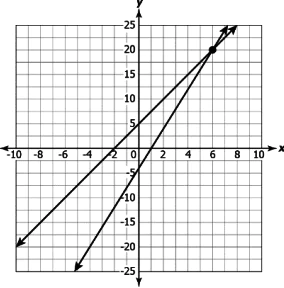
Hint: State the properties of linear equation in order to classify the given equations as linear or non linear.
Question.1. Which of these is a linear equation in two variables?
(a) 5x-2y=0
(b) x+x^{2}-2y+8=0
(c) x-2y+10=x^{2}+y
(d) 3x-2y+1=0
Question.2. If x^{2n}-1+y^{m-4}=0 is a linear equation, which of these is also a linear equation?
(a) x^{n}+y^{m}=0
(b) x^{\frac{n}{5}}+y^{\frac{m}{5}}=0
(c) x^{n+\frac{1}{2}}+y^{m+4}=0
(d) x^{\frac{1}{n}}+y^{\frac{m}{5}}=0
Ans.1. (a) 5x-2y=0
Ans.2. (d) x^{\frac{1}{n}}+y^{\frac{m}{5}}=0
Hint: Interpret the concepts of linear equations in order to represent any given situation algebraically and graphically.
Question.3. Rohit earned ₹3550 by selling some bags each for ₹500 and some baskets each for ₹150. Aarav earned ₹3400 by selling the same number of bags each for ₹400 and the same number of baskets each for ₹ 200 as Rohit sold. Which of these equations relates the number of bags x, and the number of baskets, y?
(a) 500x+150y=3550 and 400x+200y=3400
(b) 500x+150y=3400 and 400x+200y=3550
(c) 400x+150y=3550 and 500x+200y=3400
(d) 500x+200y=3550 and 400x+150y=3400
Question.4. The cost of production per unit for two products, A and B, are ₹100 and ₹80 respectively. In a week, the total production cost is ₹32000. In the next week, the production cost reduces by 20%, and the total cost of producing the same number of units of each product is ₹25600. Which of these are the equations that can be used to find the number of units of A, x, and the number of units of B, y?
(a) 100x+80y=25600 and 80x+64y=32000
(b) 100x+64y=32000 and 80x+100y=25600
(c) 80x+80y=32000 and 100x+64y=25600
(d) 100x+80y=32000 and 80x+64y=25600
Ans.3. (a) 500x+150y=3550 and 400x+200y=3400
Ans.4. (d) 100x+80y=32000 and 80x+64y=25600
Hint: Demonstrate given two linear equations in order to comment on the nature / behaviour of the lines representing the linear equations.
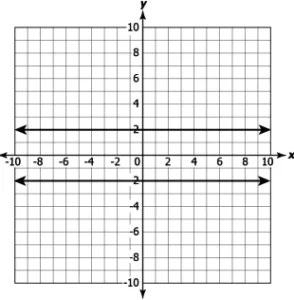
Question.5. Which of these linear equations have a unique solution?
(a) 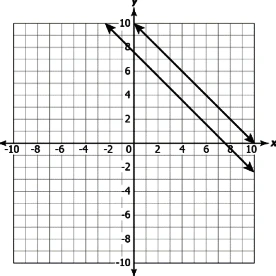
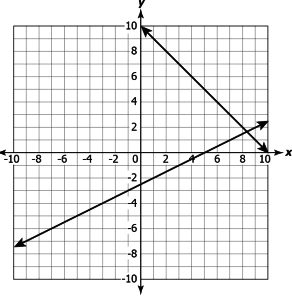
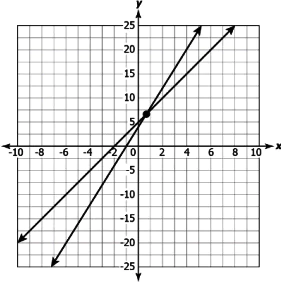
Question.6. Consider the graph shown. 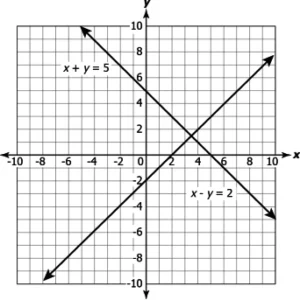
(a) These lines have a unique solution as they are intersecting at a point.
(b) These lines have infinitely many solutions as they lie in the same quadrant.
(c) These lines have a unique solution as the coefficient of x in both the equations is one.
(d) These lines have infinitely many solutions as they lie in the same quadrant.
Ans.5. (b) 
Hint: Use different algebraic methods in order to solve a pair of linear equations.
Question.7. Consider the equations shown.
4x+3y=41 and
x+3y=26
Which of these is the correct way of solving the given pair of equations?
(a) 4x-x+3y-3y=41-26
(b) 4(x+3y)+3y=41
(c) 4x+x+3y-3y=41-26
(d) 4x+3y+3y=41-26
Question.8. In the equations shown below, a and b are unknown constants.
3ax+4y=-2 and
2x+by=14
If (–3, 4) is the solution of the given equations, what are the values of a and b?
(a) a=2, b=5
(b) a=-2, b=5
(c) a=5, b=2
(d) a=5, b=-2
Ans.7. (a) 4x-x+3y-3y=41-26
Ans.8. (a) a=2, b=5
Hint: Use the most appropriate algebraic method in order to solve the given pair of linear equations.
Question.9. Consider the equations shown.
p+q=5 &
p-q=2
Which of these are the values of p and q?
(a) p=3.5, q=1.5
(b) p=1.5, q=3.5
(c) p=4, q=2
(d) p=2, q=4
Question.10. Consider the equations shown:
ax+by=ab &
2ax+3by=3b
Which of these is the value of y in terms of a?
(a) y=2a-35
(b) y=2ab-3b
(c) y=9a-35
(d) y=3-2a
Ans.9. (a) p=3.5, q=1.5
Ans.10. (d) y=3-2a
Hint: Use the concepts of pair of linear equations in two variables in order to represent any given situation algebraically and find its solution.
Question.11. Shivi gave a note of ₹2,000 for a pair of jeans worth ₹500. She was returned 11 notes in denominations of ₹200 and ₹100. Which pair of equations can be used to find the number of ₹200 notes, x, and the number of ₹100 notes x? How many notes of ₹200 did she get?
(a) x+y=11 and 200x+100y=1500; 8
(b) y=x+11 and 200x+100y=2000; 4
(c) x+y=11 and 200x+100y=1500; 4
(d) x+y=11 and 100x+200y=2000; 10
Question.12. Arnav wants to plant some saplings in columns. If he increases the number of saplings in a column by 4, the number of columns decreases by 1. If he decreases the number of saplings by 5 in a column, the number of columns increased by 2.
Which of these graphs relates the number, x, of columns and the number, y, of plants in a column?
(a) 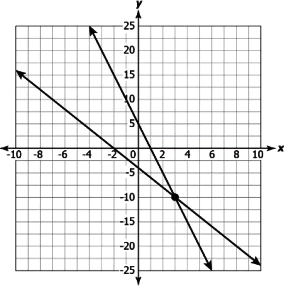
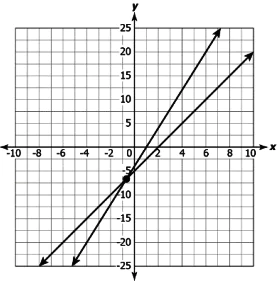
Ans.11. (c) x+y=11 and 200x+100y=1500; 4
Ans.12. (d)
Hint: Calculate the ratio of coefficients of linear equations in order to discuss the nature of pair of linear equations.
Question.13. Consider the equations as shown:
9x+6y=5 and
3x+2y=7
Which of these is true about the given equations?
(a) This is a pair of coincident lines as \frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}
(b) This is a pair of Intersecting lines as \frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}
(c) This is a pair of coincident lines as \frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}
(d) This is a pair of parallel lines as \frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}\neq \frac{c_{1}}{c_{2}}
Question.14. Consider the equations as shown:
(x-a)(y-b)=(x-2a)(y-\frac{b}{2}) and
x(x+\frac{1}{2b})+y(y+\frac{a}{2})-2xy=5+(x-y)^{2}
On comparing the coefficients, a student says these pairs of equations is consistent. Is he/she correct? Which of these explains why?
(a) Yes; because they are intersecting lines.
(b) Yes; because they are parallel lines.
(c) No; because they are parallel lines.
(d) No; because they are intersecting lines.
Ans.13. (d) This is a pair of parallel lines as \frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}\neq \frac{c_{1}}{c_{2}}
Ans.14. (a) Yes; because they are intersecting lines.
Hint: Rewrite the given equations (using substitution method) which are reducible to a pair of linear equations in order to find the solution of those equations.
Question.15. Consider a pair of equations as shown.
\frac{7}{x+2}+\frac{2}{y-2}=\frac{33}{20} and
\frac{2}{x+2}+\frac{6}{y-2}=\frac{23}{20}
Which of these pair of equations is equivalent to the given pair of equations?
(a) 7u+2v=\frac{20}{33} and 2u+6v=\frac{20}{23}
(b) 7u+6v=\frac{33}{20} and 2u+2v=\frac{23}{20}
(c) 7u+2v=\frac{33}{20} and 2u+6v=\frac{23}{20}
(d) 2u+6v=\frac{33}{20} and 7u+2v=\frac{23}{20}
Question.16. Consider a pair of equations as shown.
\frac{5}{x+2}+\frac{7}{y+2}=\frac{31}{12} and
\frac{4}{x+2}+\frac{3}{y+2}=\frac{17}{12}
What is the value of x and y ?
(a) x=2 and y=4
(b) x=4 and y=2
(c) x=14 and y=16
(d) x=16 and y=14
Ans.15. (c) 7u+2v=\frac{33}{20} and 2u+6v=\frac{23}{20}
Ans.16. (b) x=4 and y=2