Hint: Describe trigonometry in order to study the relationship between side and angle of a triangle.
Question.1. Which of the following completes the statement below?
The adjacent and ______ of right triangle depends on the \angle x being referred to in that triangle and for the complementary angle (90 − 𝑥)° & of that triangle, the adjacent and opposite are ___________.
(a) opposite side, reversed
(b) opposite side, same
(c) hypotenuse, reversed
(d) hypotenuse, same
Question.2. Considering the diagram below. 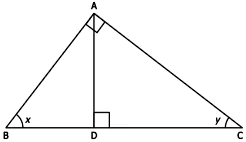
(a) Side AC is adjacent to \angle y in triangle ADC and triangle ABC
(b) Side AC is adjacent to \angle y in triangle ADC and side BC is adjacent to \angle y in triangle ABC
(c) Side DC is adjacent to \angle y in triangle ADC and side AC is adjacent to \angle y in triangle ABC
(d) Side AC is adjacent to \angle y in triangle ADC and side DC is adjacent to \angle y in triangle ABC
Ans.1. (a) opposite side, reversed
Ans.2. (c) Side DC is adjacent to \angle y in triangle ADC and side AC is adjacent to \angle y in triangle ABC
Hint: Define and distinguish various trigonometric ratios in order to describe and verify sine, cosine, tangent, cosecant, secant, cotangent of an angle.
Question.3. Consider the triangle shown below. 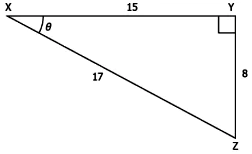
(a) tan θ = \frac{8}{15}, cosec θ = \frac{17}{15}, sec θ = \frac{17}{8}
(b) tan θ = \frac{8}{15}, cosec θ = \frac{17}{8}, sec θ = \frac{17}{15}
(c) tan θ = \frac{17}{15}, cosec θ = \frac{8}{15}, sec θ = \frac{17}{8}
(d) tan θ = \frac{8}{15}, cosec θ = \frac{17}{15}, sec θ = \frac{8}{17}
Question.4. Observe the figure shown. 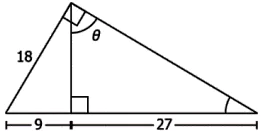
(a) \frac{1}{2}
(b) \frac{2}{1}
(c) \frac{2\sqrt{3}}{3}
(d) \frac{3\sqrt{3}}{2}
Ans.3. (b) tan θ = \frac{8}{15}, cosec θ = \frac{17}{8}, sec θ = \frac{17}{15}
Ans.4. (a) \frac{1}{2}
Hint: Use given trigonometric ratio(s) in order to find and verify other trigonometric ratios/angles of the triangle.
Question.5. If sin θ = \frac{7}{\sqrt{85}}, what are the values of tan θ, cos θ and cosec θ?
(a) tan θ = \frac{7}{6}, cos θ =\frac{6}{\sqrt{85}} and cosec θ = \frac{\sqrt{85}}{7}
(b) tan θ = \frac{6}{7}, cos θ =\frac{7}{\sqrt{85}} and cosec θ = \frac{\sqrt{85}}{7}
(c) tan θ = \frac{7}{6}, cos θ =\frac{7}{\sqrt{85}} and cosec θ = \frac{\sqrt{85}}{7}
(d) tan θ = \frac{6}{7}, cos θ =\frac{6}{\sqrt{85}} and cosec θ = \frac{\sqrt{85}}{6}
Question.6. The two legs AB and BC of right triangle ABC are in a ratio 1:3. What will be the value of sin C?
(a) \frac{1}{\sqrt{10}}
(b) \frac{3}{\sqrt{10}}
(c) \frac{1}{3}
(d) \frac{1}{2}
Ans.5. (a) tan θ = \frac{7}{6}, cos θ =\frac{6}{\sqrt{85}} and cosec θ = \frac{\sqrt{85}}{7}
Ans.6. (a) \frac{1}{\sqrt{10}}
Hint: Compute the trigonometric ratio of 0°, 30°, 45°, 60°, 90° in order to know and apply the value of specific angles.
Question.7. What is the value of \frac{3-\sin^{2}60°}{\tan 30° \tan 60°}?
(a) 1\frac{1}{4}
(b) 2\frac{1}{4}
(c) 2\frac{1}{2}
(d) 2\frac{3}{4}
Question.8. The value of \frac{4-\sin^{2}45°}{\cot k \tan 60°} is 3.5.
What is the value of k?
(a) 30°
(b) 60°
(c) 45°
(d) 90°
Ans.7. (b) 2\frac{1}{4}
Ans.8. (b) 60°
Hint: Compute the trigonometric ratio of complimentary angles in order to apply the values in mathematical problems.
Question.9. What is the value of \frac{5 \csc 55°}{\sec 35°}?
(a) \frac{5}{2}
(b) \frac{15}{2}
(c) 5
(d) 15
Question.10. If \sec 2x = \frac{1}{\sin (x-36)°}, where 2x is an acute angle, what is the value of x?
(a) 36
(b) 42
(c) 48
(d) 52
Ans.9. (b) \frac{15}{2}
Ans.10. (b) 42
Hint: Compute and apply trigonometric identities in order to simplify and solve mathematical problems.
Question.11. Which of these is equivalent to \frac{2 \tan x (\sec^{2}x-1)}{\cos^{3}x}?
(a) 2 \tan^{3}x \csc x
(b) 2 \tan^{3}x \sec^{3} x
(c) 2 \tan^{3}x \csc^{3} x
(d) 2 \cot^{3}x \sec^{3} x
Question.12. Which of the following option makes the statement below true?
\frac{\frac{1}{\sec x}+\sec x}{\cos^{2}x-1-\tan^{2}x} = ?
(a) −cosec x cot x
(b) − sec x cot x
(c) −cosec x tan x
(d) − sec x tan x
Ans.11. (b) 2 \tan^{3}x \sec^{3} x
Ans.12. (a) −cosec x cot x
