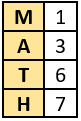
Hint: Understand the predecessor of One in order to know the whole number.
Question.1. Predecessor of which of these numbers is a whole number and NOT a natural number?
(a) 0
(b) 1
(c) 10
(d) 100
Question.2. Which of the following statements is true?
(a) Predecessor of any natural number is the smallest whole number.
(b) Predecessor of the smallest natural number is the smallest whole number.
(c) Predecessor of a natural number can never be a whole number.
(d) Predecessor of the smallest whole number is the smallest natural number.
Ans.1. (b) 1
Ans.2. (b) Predecessor of the smallest natural number is the smallest whole number.
Hint: Explain the whole number in order to know the predecessor of 1 and the subtraction of the two same number.
Question.3. Which of these expressions represents the least whole number?
(a) 1 + 0
(b) 0 – 1
(c) 10 ✕ 1
(d) 12 – 12
Question.4. Consider the statement below.
“Every whole number has a whole number as its predecessor” Which of these is a valid conclusion about the statement?
(a) Yes, because the predecessor of 0 is a whole number.
(b) No, because the predecessor of 0 is not a whole number.
(c) No, because the predecessor of 1 is not a whole number.
(d) Yes, because the predecessor of any whole number is a whole number.
Ans.3. (d) 12 – 12
Ans.4. (a) Yes, because the predecessor of 0 is a whole number.
Hint: Define unit distance in order to construct the number line.
Question.5. Aryan plotted whole numbers 0 to 7 on a number line. How many unit distances did he draw?
(a) 0
(b) 1
(c) 7
(d) 8
Question.6. Consider the statement below. “A student plotted 5 consecutive even whole numbers on a number line.” Which of these is a valid conclusion about any 2 consecutive even numbers?
(a) They are separated by 1 unit.
(b) They are separated by 2 units.
(c) They are separated by 5 units.
(d) They are separated by 10 units.
Ans.5. (c) 7
Ans.6. (b) They are separated by 2 units.
Hint: Draw the Number line in order to represent the whole number.
Question.7. If X and Y two consecutive whole numbers, how many whole numbers can be shown on the number line below?
(a) 2
(b) 5
(c) 7
(d) 8
Question.8. Observe the number line below.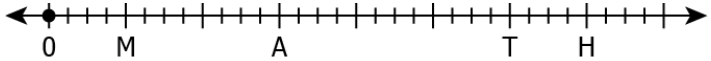
(a) 
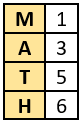
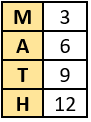
Ans.7. (c) 7
Ans.8. (d)
Hint: Draw a number line in order to find the predecessor and successor of a given number.
Question.9. Which of these number lines shows the predecessor of 23?
(a) 
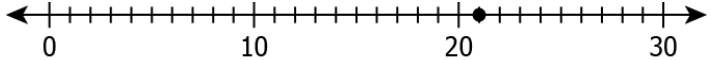

Question.10. Consider the statement below. “Successor of the predecessor of 14.” Which of these number lines correctly represents the number in the statement?
(a) 

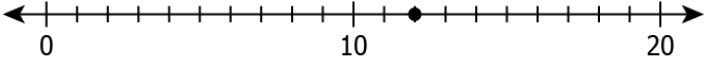
Ans.9. (d) 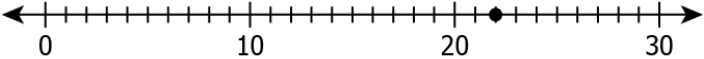
Hint: Represent the Numbers on Number line in order to perform number operation.
Question.11. Which number line shows the 5 times 3?
(a) 


Question.12. Which operation of numbers does this number line represent?
(a) 7 – 5 + 10
(b) 7 – 5 + 5
(c) 7 – 2 + 10
(d) 7 – 2 + 5
Ans.11. (d) 
Hint: Apply properties of whole number in order to simplify arithmetic expression.
Question.13. Raghav solves the expression 5 × (1 + 4) as u + v. Which option is true for the values of u and v?
(a) u = 5; v = 4
(b) u = 5; v = 20
(c) u = 5; v = 5
(d) u = 6; v = 20
Question.14. Consider the following claims.
Claim 1: (16 + 9) + 2 = 16 + (9 + 2) = 27 shows associativity of addition for whole numbers
Claim 2: 13 – 61 = – 48 shows the closure property of whole numbers under subtraction
Claim 3: 5 × 4 = 20 shows the closure property of whole numbers under multiplication
Which option is correct?
(a) Only claim 2 is correct
(b) Only claim 1 and 2 are correct
(c) Only claim 1 and 3 are correct
(d) All claims are correct
Ans.13. (b) u = 5; v = 20
Ans.14. (c) Only claim 1 and 3 are correct
Hint: Represent numbers in order to form line, rectangle, triangle and a square.
Question.15. How many dots can be arranged such that there should be the same number of dots in each row and column?
(a) 12
(b) 15
(c) 16
(d) 20
Question.16. Consider the following claims.
Claim 1: Numbers 36, 45, 55 and 66 are forming pattern of triangular numbers.
Claim 2: Numbers 20, 28, 34 and 42 are forming pattern of rectangular numbers.
Which option is true about the claims?
(a) Only Claim 1 is correct
(b) Only Claim 2 is correct
(c) Both Claim 1 and Claim 2 are correct
(d) Neither Claim 1 nor Claim 2 is correct
Ans.15. (c) 16
Ans.16. (c) Both Claim 1 and Claim 2 are correct
Hint: Form number patterns in order to verbal calculation and to understand numbers better.
Question.17. Observe the pattern below.
34 × 5 = 34 × \frac{10}{2} = 17 × 10 = 170 × 1
34 × 15 = 34 × \frac{30}{2} = 17 × 30 = 170 × 3
Which of these options completes the pattern 34 × 45 = ___?
(a) 34 × \frac{50}{2} = 17 × 50 = 170 × 5
(b) 34 × \frac{45}{2} = 17 × 45 = 85 × 9
(c) 34 × \frac{90}{2} = 17 × 90 = 170 × 9
(d) 34 × \frac{110}{2} = 17 × 110 = 170 × 11
Question.18. Observe the pattern below. 91 × 9 = 91 × (100 – 1) = 9100 – 91 = 9009. Which of these is equivalent to 91 × 9999?
(a) 91 × (1000 – 1) = 91000 – 91 = 90909
(b) 91 × (1000 + 1) = 91000 + 91 = 91091
(c) 91 × (10000 – 1) = 910000 – 91 = 909909
(d) 91 × (10000 + 1) = 910000 + 91 = 910091
Ans.17. (c) 34 × \frac{90}{2} = 17 × 90 = 170 × 9
Ans.18. (c) 91 × (10000 – 1) = 910000 – 91 = 909909