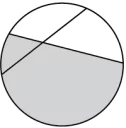
Hint: Represent a number as a part of the whole in order to determine the fraction.
Question.1. A rectangle is divided into equal parts as shown: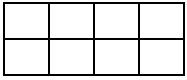
(a) \frac{3}{5}
(b) \frac{5}{3}
(c) \frac{3}{8}
(d) \frac{5}{8}
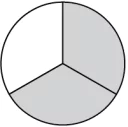
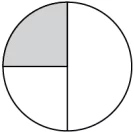
Question.2. In which of the following models, the fraction represented by shaded portion is the same as the fraction represented by unshaded portion?
(a) 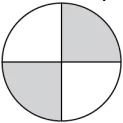
Ans.1. (d) \frac{5}{8}
Ans.2. (a)
Hint: Determine part and whole in order to label numerator and denominator of a fraction.
Question.3. Ajay wants to represents a fraction \frac{3}{5} in a rectangular model. What is the minimum number of equal parts he needs to divide the rectangular model into?
(a) 2
(b) 3
(c) 5
(d) 8
Question.4. Ajay divided a square into b equal parts and shaded a parts. Which of these represents the numerator of the fraction that represents the unshaded portion?
(a) a
(b) a-b
(c) b-a
(d) a+b
Ans.3. (c) 5
Ans.4. (c) b-a
Hint: Draw equal parts between the whole numbers in order to represent fractions on a number line.
Question.5. A number line is divided into equal parts and a point P is plotted on it as shown.
(a) \frac{3}{7}
(b) \frac{3}{8}
(c) \frac{4}{8}
(d) \frac{4}{9}
Question.6. Akriti followed the given steps to represent a fraction on a number line.
Step 1: Using tick marks, she divided the number line between 0 and 1 into 5 equal parts.
Step 2: She plotted a point at the 4th tick mark to the right of 0.
What fraction does the point show?
(a) \frac{1}{5}
(b) \frac{3}{5}
(c) \frac{4}{5}
(d) \frac{4}{9}
Ans.5. (b) \frac{3}{8}
Ans.6. (c) \frac{4}{5}
Hint: Write proper fractions in order to deduce that they are always less than 1 or numerator is less than denominator.
Question.7. If \frac{m}{4} is a proper fraction, which option shows the possible values of m?
(a) 1, 2 and 3
(b) 1, 2, 3 and 4
(c) 5, 6 and 7
(d) 4, 5, 6 and 7
Question.8. Which of these will always be a proper fraction for any natural number m>1?
(a) \frac{m}{m+1}
(b) \frac{m+1}{m}
(c) \frac{m}{m}
(d) \frac{m}{m-1}
Ans.7. (a) 1, 2 and 3
Ans.8. (a) \frac{m}{m+1}
Hint: Write fractions where numerator is greater than denominator in order to determine improper fractions.
Question.9. For what value of s and t, \frac{s}{t} will be an improper fraction?
(a) s=3, t=3
(b) s=3, t=5
(c) s=0, t=5
(d) s=5, t=3
Question.10. If the fraction \frac{6}{y} is an improper fraction, which of these could be the value of y?
(a) 4
(b) 6
(c) 9
(d) 12
Ans.9. (d) s=5, t=3
Ans.10. (a) 4
Hint: Write the improper fraction in the form of mixed fraction in order to represent it as a combination of whole and a part.
Question.11. If the fraction \frac{119}{19} is represented in the form of j\frac{k}{19}, what is the value of j and k?
(a) j=10, k=0
(b) j=5, k=6
(c) j=6, k=5
(d) j=6, k=6
Question.12. If 4\frac{k}{13} can also be written as \frac{59}{13}, what is the value of k?
(a) 4
(b) 5
(c) 6
(d) 7
Ans.11. (c) j=6, k=5
Ans.12. (d) 7
Hint: Multiply/Divide the numerator and denominator with the same number in order to find equivalent fractions.
Question.13. If \frac{3}{t} and \frac{51}{119} are equivalent fractions, what is the value of t?
(a) 3
(b) 7
(c) 8
(d) 17
Question.14. A teacher creates an assignment consisting of 19 questions. Of these 19 questions, 7 were easy. The teacher now needs to create another assignment and wants the fraction of easy questions in this assignment to be the same as in the previous one. If the new assignment will have a total of 76 questions, how many easy questions will be there in the assignment?
(a) 7
(b) 11
(c) 19
(d) 28
Ans.13. (b) 7
Ans.14. (d) 28
Hint: Perform cross multiplication among two fractions in order to verify their equivalence.
Question.15. Which of the following must be true for fractions \frac{x}{6} and \frac{12}{y} to be equivalent?
(a) The sum of x and y is equal to 18.
(b) The sum of x and y is equal to 72.
(c) The product of x and y is equal to 18.
(d) The product of x and y is equal to 72.
Question.16. Consider the fractions \frac{a}{b}, \frac{c}{d} and \frac{p}{q} and the following relationships.
Relation 1: a\times d=a\times q=c\times q =12
Relation 2: b\times c=b\times p=d\times p =12
Which of the given relations verify that the fractions are equivalent?
(a) Both relations together are sufficient, but neither relation is sufficient alone
(b) Relation 2 is sufficient alone, but not Relation 1
(c) Relation 1 is sufficient alone, but not Relation 2
(d) Relations 1 and 2 together are not sufficient
Ans.15. (d) The product of x and y is equal to 72.
Ans.16. (a) Both relations together are sufficient, but neither relation is sufficient alone
Hint: Reduce the fraction in order to determine its simplest form.
Question.17. Which of these shows the way to express \frac{16}{24} in its simplest form?
(a) Divide 16 and 24 by their HCF
(b) Divide 16 and 24 by their LCM
(c) Multiply 16 and 24 by their LCM
(d) Multiply 16 and 24 by their HCF
Question.18. The HCF of numbers a and b is 5. If the simplest form of fraction \frac{a}{b} is \frac{8}{19}, what could be the fraction?
(a) \frac{3}{14}
(b) \frac{8}{19}
(c) \frac{13}{24}
(d) \frac{40}{95}
Ans.17. (a) Divide 16 and 24 by their HCF
Ans.18. (d) \frac{40}{95}
Hint: Check the denominators of the fractions in order distinguish between like and unlike fractions.
Question.19. Amrita writes a fraction which is the simplest form of \frac{5}{15}. If the fraction she writes and \frac{2}{b} are like fractions, which of these can be the value of b?
(a) 1
(b) 2
(c) 3
(d) 5
Question.20. If the fractions \frac{3}{5} and \frac{m}{n} are unlike fractions (n ≠ 0), which of these shows the possible values of m and n?
(a) m=3; n=5
(b) m can take any value except 3; n=5
(c) m=3, n can take any value except 5
(d) m can take any value, n can take any value except 5
Ans.19. (c) 3
Ans.20. (d) m can take any value, n can take any value except 5
Hint: Inspect the numerators of the like fractions in order to determine larger and smaller fraction(s).
Question.21. If the fraction \frac{m}{9} is greater than \frac{6}{9}, which of these shows the value of m?
(a) 0 < m < 3
(b) 0 < m < 6
(c) 3 < m < 9
(d) 6 < m < 9
Question.22. If the fraction \frac{9}{m} is less than \frac{k}{m}, which of these can be the value of k?
(a) 1
(b) 4
(c) 9
(d) 15
Ans.21. (d) 6 < m < 9
Ans.22. (d) 15
Hint: Determine the LCM of the unlike fractions in order to compare them.
Question.23. Which option correctly arranges the fractions \frac{2}{5}, \frac{2}{6} and \frac{7}{15} in increasing order?
(a) \frac{2}{5} < \frac{2}{6} < \frac{7}{15}
(b) \frac{2}{6} < \frac{2}{5} < \frac{7}{15}
(c) \frac{7}{15} < \frac{2}{5} < \frac{2}{6}
(d) \frac{7}{15} < \frac{2}{6} < \frac{2}{5}
Question.24. Which of the following is true about the fractions M and N shown below?
M = 2\frac{5}{8}
N = 2\frac{4}{5}
(a) M<N, because \frac{5}{8} < \frac{4}{5}
(b) M=N, because their whole parts are equal
(c) M>N, because \frac{5}{8} > \frac{4}{5}
(d) M and N can’t be compared because they are mixed numbers
Ans.23. (b) \frac{2}{6} < \frac{2}{5} < \frac{7}{15}
Ans.24. (a) M<N, because \frac{5}{8} < \frac{4}{5}
Hint: Solve (addition/subtraction) the numerator and retain the denominator of the like fractions in order to perform addition and subtraction on the given fraction.
Question.25. If the difference of like fractions \frac{7}{m} and \frac{3}{n} is \frac{4}{11}, which of the following is true about m and n?
(a) m-n=11
(b) m+n=11
(c) m=n=4
(d) m=n=11
Question.26. Which of these shows the sum of like fractions \frac{3}{7} and \frac{p}{q}?
(a) \frac{3p}{7}
(b) \frac{3+p}{7}
(c) \frac{3}{7+q}
(d) \frac{3+p}{7+q}
Ans.25. (d) m=n=11
Ans.26. (b) \frac{3+p}{7}
Hint: Convert the given fractions into its equivalent fractions in order to perform addition and subtraction on them.
Question.27. The total distance between Ajay’s home and his office is 3\frac{1}{6} km. He covered first \frac{1}{2} km walking and then took a bus. He again walks for \frac{2}{3} km to reach his office. What is the distance that Ajay covered by bus?
(a) 1\frac{2}{3} km
(b) 2 km
(c) 2\frac{1}{2} km
(d) 4 km
Question.28. The steps followed by a student to subtract 1\frac{7}{8} from 3\frac{3}{4} are shown below:
Step 1: 3\frac{3}{4} – 1\frac{7}{8}
Step 2: (3-1)+\left(\frac{3}{4}-\frac{7}{8}\right)
Step 3: 2+\left(\frac{6}{8}-\frac{7}{8}\right)
Step 4: 2+\left(\frac{7-6}{8}\right)
Step 5: 2\frac{1}{8}
In which step did the student make her first error? What is the correct step?
(a) Step 2; \left(\frac{15}{4}-\frac{15}{8}\right)
(b) Step 2; (3-1)+\left(\frac{3}{4}+\frac{7}{8}\right)
(c) Step 3; 2+\left(\frac{7}{8}-\frac{6}{8}\right)
(d) Step 3; 2+\left(\frac{3}{8}-\frac{6}{8}\right)
Ans.27. (b) 2 km
Ans.28. (a) Step 2; \left(\frac{15}{4}-\frac{15}{8}\right)