Hint: Construct a circle of a given radius in order to verify that the length of multiple segments drawn from the centre of the circle to the circumference is equal.
Question.1. Given below is a circle with radius OA.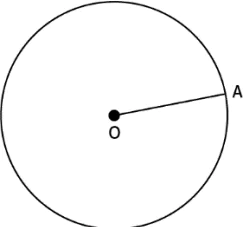
(a) OA = OP
(b) OA = 2 OP
(c) OA = \frac{1}{2} OP
(d) OA = \frac{1}{3}OP
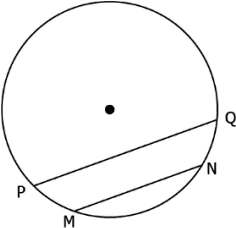
Question.2. Given below is a circular park with centre A. Madhav walks at a uniform speed of 0.5 m/s from Gate P and reaches the centre of the park in 150 seconds.
(a) 300 m
(b) 150 m
(c) 2.5 m
(d) 75 m
Ans.1. (a) OA = OP
Ans.2. (d) 75 m
Hint: Define radius, chord, diameter, segment (major and minor), arc (major and minor), interior or exterior of a circle in order to illustrate and label them on a given circle.
Question.3. Given below is a circle with center O.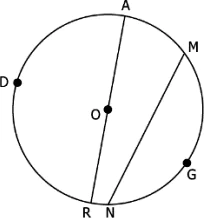
(a) MGN is the minor sector
(b) \widehat{MN} is the minor arc
(c) \widehat{MDN} is the major arc
(d) AR is a chord
Question.4. Given below are two circles with center A and D.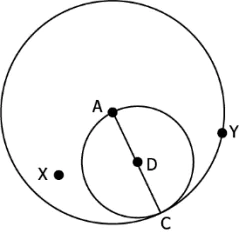
(a) Point X lies inside the bigger circle.
(b) AC is a chord of the smaller circle.
(c) AC is the radius of the bigger circle.
(d) Smaller circle lies in the minor segment of the bigger circle.
Ans.3. (a) MGN is the minor sector
Ans.4. (d) Smaller circle lies in the minor segment of the bigger circle.
Hint: Apply theorems regarding angle subtended by a chord in a circle in order to find the measure of an angle in the given figure.
Question.5. Given below is a circle with centre O.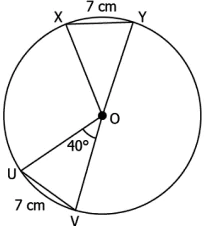
(a) 40°
(b) 140°
(c) 80°
(d) 90°
Question.6. In the figure below, PQ and RS are equal chords of a circle with centre T.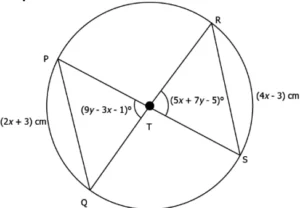
(a) 100°
(b) 40°
(c) 80°
(d) 60°
Ans.5. (a) 40°
Ans.6. (c) 80°
Hint: Apply the property of perpendicular from the centre to the chord in order to solve for the missing values (lengths and angles) in a given figure.
Question.7. Given below is a circle with centre A and chord BC.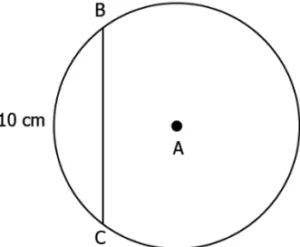
(a) 10 cm
(b) 13 cm
(c) 12 cm
(d) 5 cm
Question.8. Given below is a circle with diameter 20 cm.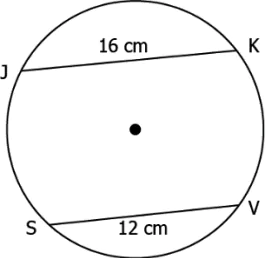
(a) 14 cm; it will increase by 12 cm
(b) 7 cm; it will remain same
(c) 14 cm; it will decrease by 12 cm
(d) 2 cm; it will increase by 12 cm
Ans.7. (c) 12 cm
Ans.8. (c) 14 cm; it will decrease by 12 cm
Hint: Construct circle passing through 1, 2 & 3 non-collinear points in order to comment on how many circles can be constructed passing through them.
Question.9. Which statement is not correct?
(a) Infinitely many circles can pass through all the points A, B and C.
(b) Infinitely many circles can pass through both the points A and B.
(c) Infinitely many circles can pass through the point A.
(d) Only two circles can pass through both the points B and C.
Question.10. How many circle(s) can be constructed that passes through each vertex of ∆PQR?
(a) 4
(b) 3
(c) Infinitely many
(d) 1
Ans.9. (a) Infinitely many circles can pass through all the points A, B and C.
Ans.10. (d) 1
Hint: Use the value of radius and perpendicular to the chord in order to compute the length of a chord.
Question.11. Given below is a circle with centre A and radius 10 cm.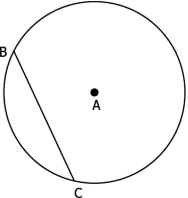
(a) 6 cm
(b) 12 cm
(c) 5 cm
(d) 4 cm
Question.12. Given below is a circle with radius 13 cm. PQ and MN are two chords of length 24 cm and x cm respectively. The distance between the chords is 7 cm. What is the value of x?
(a) 10 cm
(b) 5 cm
(c) 11 cm
(d) 6 cm
Ans.11. (b) 12 cm
Ans.12. (a) 10 cm
Hint: Interpret and apply theorems on the angles subtended by arcs of a circle in order to solve for unknown values in given examples.
Question.13. In the figure below, AN and MD are equal chords of a circle with centre O and diameter 20 cm.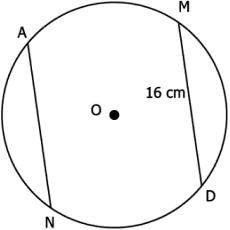
(a) 10 cm
(b) 12 cm
(c) 6 cm
(d) 25 cm
Question.14. Given below is a quadrilateral PQRS in a circle with centre T.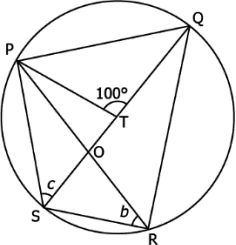
(a) b=50° and c=40°
(b) b=80° and c=100°
(c) b=100° and c=80°
(d) b=40° and c=50°
Ans.13. (b) 12 cm
Ans.14. (d) b=40° and c=50°
Hint: Apply the relation between angles of a cyclic quadrilateral in order to solve for the value of a given angle.
Question.15. In the figure below,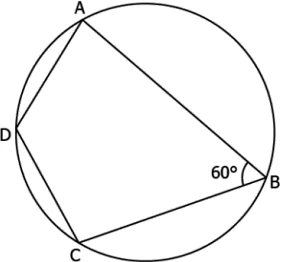
What are the measures of \angleC and \angleD?
(a) \angleC = 120° and \angleD = 108°
(b) \angleC = 108° and \angleD = 120°
(c) \angleC = 120° and \angleD = 108°
(d) \angleC = 72° and \angleD = 120°
Question.16. Given below is a circle with centre O.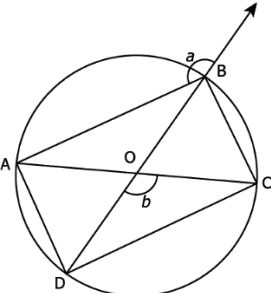
(a) 180° +\left(a-\frac{b}{2}\right)
(b) 180° -\left(a+\frac{b}{2}\right)
(c) 180° – a-\frac{b}{2}
(d) 180° -\left(a-\frac{b}{2}\right)
Ans.15. (b) \angleC = 108° and \angleD = 120°
Ans.16. (d) 180° -\left(a-\frac{b}{2}\right)