Competency Based Questions of Maths for Class 10 Chapter 11 Areas Related to Circles

Competency Based Questions are new type of questions asked in CBSE Board exam for class 10. Practising the following Competency Based Questions will help the students in facing Board Questions.

Hint: Describe the relationship between circumference and diameter of a circle in order to define \pi .

Question.1. Which of these is equivalent to \pi ?

(a) \frac{Circumference}{radius}
(b) Circumference \times diameter
(c) \frac{Circumference}{diameter}
(d) Circumference \times radius

Answer. (c) \frac{Circumference}{diameter}

Question.2. Raman draws a circle with diameter 6 units. He draws another circle by increasing the radius of the previously drawn circle by 4 units. What would be the quotient if he divides the circumference of the newly formed circle by its diameter?

(a) \pi
(b) 2\pi
(c) 8
(d) 12

Answer. (a) \pi

Hint: Apply the concepts of circumference and area of in order to solve in for various circular objects in real life.

Question.3. A circular garden, of circumference 88 m is surrounded by a pathway of width 3.5 m. Ajay wants to put fence around the pathway. What is the cost of fencing the pathway at the rate of ₹70 per metre? (Use \pi =\frac{22}{7})

(a) ₹3,080
(b) ₹3,850
(c) ₹6,160
(d) ₹7,700

Answer. (d) ₹7,700

Question.4. A fountain is enclosed by a circular fence of circumference 11 m and is surrounded by a circular path. The circumference of the outer boundary of the path is 16 m. A gardener increased the width of the pathway by decreasing the area enclosed by the fence such that the length of the fence is decreased by 3 m. The path is to be covered by the bricks which cost ₹125 per m^{2}. What will be the total cost, to the nearest whole number, required to cover the area by the bricks? (Use \frac{22}{7} for \pi )

(a) ₹79,545
(b) ₹39,772
(c) ₹9878
(d) ₹1,910

Answer. (d) ₹1,910

Hint: Describe sector and segment of a circle in order to differentiate between the two.

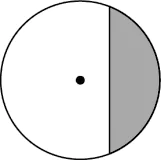
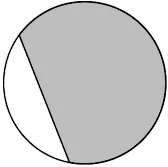
Question.5. Consider a circle below. 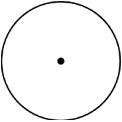Aman shades a part in the circle which is enclosed by two radii and its corresponding arc. Which of these could he have drawn?

(a)

(b)

(c)

(d)

Answer. (c)

Question.6. Consider the statements below.
Statement A: A quarter circle represents a sector of the circle.
Statement B: A semicircle represents both sector and segment of the circle.
Which of these statements is correct?

(a) Only Statement A
(b) Only Statement B
(c) Both the statements A and B
(d) Neither statement A nor B

Answer. (c) Both the statements A and B

Hint: Describe minor and major sector of a circle in order to differentiate between the two.

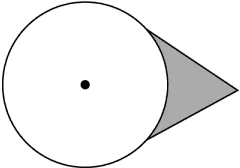
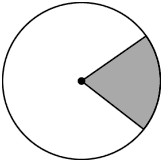
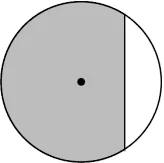
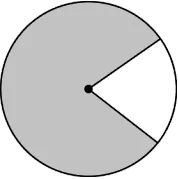
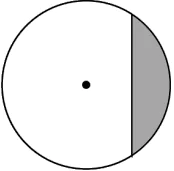
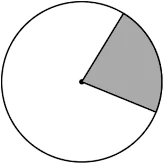
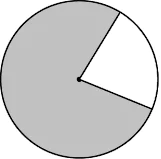
Question.7. Which of the following options represents the shaded region as the major sector and unshaded region as the minor sector?

(a)

(b)

(c)

(d)

Answer. (c)

Question.8. To form a circle of radius r, four minor sectors of equal measure are joined.
Which of these options completes the sentence below?
The sum of the area of the four minor sectors is equal to the __________.

(a) circumference of the circle of radius r.
(b) area of the semicircle of diameter 2r.
(c) area of the circle of diameter 2r.
(d) circumference of the circle of diameter r.

Answer. (c) area of the circle of diameter 2r.

Hint: Describe minor and major segment of a circle in order to differentiate between the two.

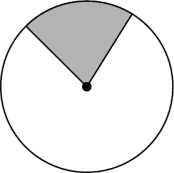
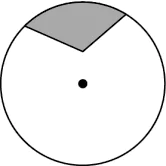
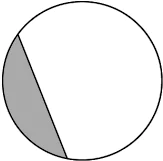
Question.9. To show the minor segment of a circle, a student shades the region enclosed between a chord and the minor arc.
Which of these shows the region the student could have shaded?

(a)

(b)

(c)

(d)

Answer. (d)

Question.10. Which of these is equivalent to the sum of the lengths of arc corresponding to the minor and major segment of a circle of radius 12 cm?

(a) 12\pi cm
(b) 24\pi cm
(c) 36\pi cm
(d) 144\pi cm

Answer. (b) 24\pi cm

Hint: Apply the formula of area of sector and segment of a circle in order to compute the area of a specified region.

Question.11. Observe the figure below: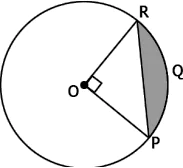 What is the area of the segment PQR, if the radius of the circle is 7 cm? (Use \pi =\frac{22}{7})

(a) 11 cm^{2}
(b) 14 cm^{2}
(c) 17.3 cm^{2}
(d) 91 cm^{2}

Answer. (b) 14 cm^{2}

Question.12. Two concentric circles of radius 8 cm and 5 cm are shown below, and a sector forms an angle of 60° at the centre O. 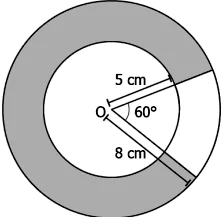What is the area of the shaded region?

(a) 38\pi cm^{2}
(b) \frac{77 \pi}{2} cm^{2}
(c) \frac{11 \pi}{2} cm^{2}
(d) \frac{195 \pi}{2} cm^{6}

Answer. (d) \frac{195 \pi}{2} cm^{2}

Hint: Calculate the length of an arc of a circle in order to comment whether it is the major arc or minor arc.

Question.13. An arc of a circle of radius 14 cm, subtends an angle of 45° at the centre as shown: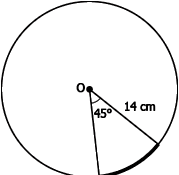 Which of these options is correct?

(a) The arc shown is a major arc and its length is 38.5 cm.
(b) The arc shown is a minor arc and its length is 11 cm.
(c) The arc shown is a minor arc and its length is 5.5 cm.
(d) The arc shown is a major arc and its length is 77 cm.

Answer. (b) The arc shown is a minor arc and its length is 11 cm.

Question.14. A circle with centre O of diameter 28 cm and a chord BC of length 14 cm is shown below: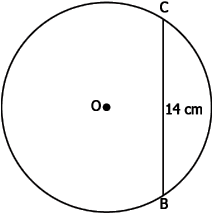 What is the length of the major arc of the circle, to the nearest tenth?

(a) 7.3 cm
(b) 14.7 cm
(c) 73.3 cm
(d) 146.7 cm

Answer. (c) 73.3 cm

Hint: Calculate the area of various combinations of plane figures in order to apply the concepts of circles, quadrilaterals and triangles.

Question.15. In equilateral triangle of side 28 cm is inscribed in a circle of diameter 32 cm, as shown below: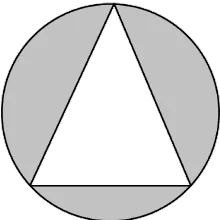 What is the area of the shaded region? (Use \pi = 3.14 and \sqrt{3}=1.73)

(a) 125.68 cm^{2}
(b) 411.84 cm^{2}
(c) 464.76 cm^{2}
(d) 2876.28 cm^{2}

Answer. (c) 464.76 cm^{2}

Question.16. Ankita shaded a square cardboard, as shown below: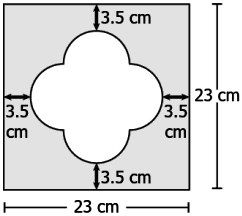 Which of these is closest to the area of the shaded region?

(a) 263.9 cm^{2}
(b) 364.4 cm^{2}
(c) 439.9 cm^{2}
(d) 492.4 cm^{2}

Answer. (b) 364.4 cm^{2}