Competency Based Questions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables
Competency Based Questions are new type of questions asked in CBSE Board exam for class 10. Practising the following Competency Based Questions will help the students in facing Board Questions.
Hint: State the properties of linear equation in order to classify the given equations as linear or non linear.
Question.1. Which of these is a linear equation in two variables?
(a) 5x-2y=0
(b) x+x^{2}-2y+8=0
(c) x-2y+10=x^{2}+y
(d) 3x-2y+1=0
Answer. (a) 5x-2y=0
Question.2. If x^{2n}-1+y^{m-4}=0 is a linear equation, which of these is also a linear equation?
(a) x^{n}+y^{m}=0
(b) x^{\frac{n}{5}}+y^{\frac{m}{5}}=0
(c) x^{n+\frac{1}{2}}+y^{m+4}=0
(d) x^{\frac{1}{n}}+y^{\frac{m}{5}}=0
Answer. (d) x^{\frac{1}{n}}+y^{\frac{m}{5}}=0
Hint: Interpret the concepts of linear equations in order to represent any given situation algebraically and graphically.
Question.3. Rohit earned ₹3550 by selling some bags each for ₹500 and some baskets each for ₹150. Aarav earned ₹3400 by selling the same number of bags each for ₹400 and the same number of baskets each for ₹ 200 as Rohit sold. Which of these equations relates the number of bags x, and the number of baskets, y?
(a) 500x+150y=3550 and 400x+200y=3400
(b) 500x+150y=3400 and 400x+200y=3550
(c) 400x+150y=3550 and 500x+200y=3400
(d) 500x+200y=3550 and 400x+150y=3400
Answer. (a) 500x+150y=3550 and 400x+200y=3400
Question.4. The cost of production per unit for two products, A and B, are ₹100 and ₹80 respectively. In a week, the total production cost is ₹32000. In the next week, the production cost reduces by 20%, and the total cost of producing the same number of units of each product is ₹25600. Which of these are the equations that can be used to find the number of units of A, x, and the number of units of B, y?
(a) 100x+80y=25600 and 80x+64y=32000
(b) 100x+64y=32000 and 80x+100y=25600
(c) 80x+80y=32000 and 100x+64y=25600
(d) 100x+80y=32000 and 80x+64y=25600
Answer. (d) 100x+80y=32000 and 80x+64y=25600
Hint: Demonstrate given two linear equations in order to comment on the nature / behaviour of the lines representing the linear equations.
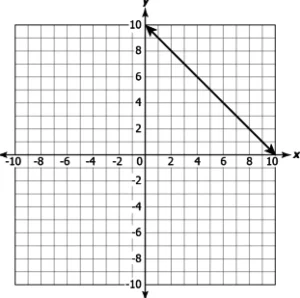
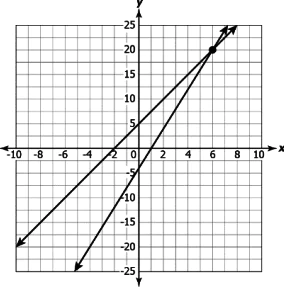
Question.5. Which of these linear equations have a unique solution?
(a) 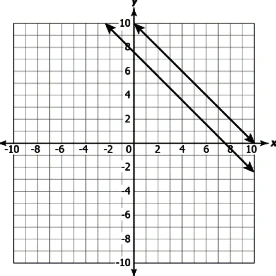
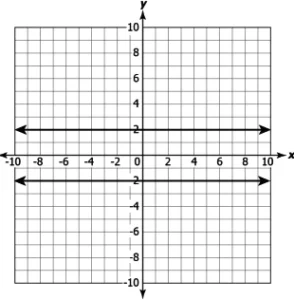
Answer. (b)
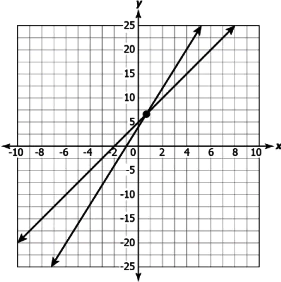
Question.6. Consider the graph shown. 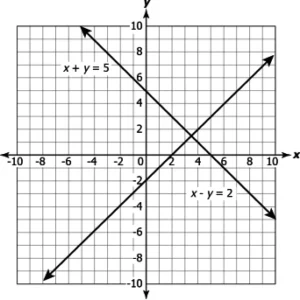
(a) These lines have a unique solution as they are intersecting at a point.
(b) These lines have infinitely many solutions as they lie in the same quadrant.
(c) These lines have a unique solution as the coefficient of x in both the equations is one.
(d) These lines have infinitely many solutions as they lie in the same quadrant.
Answer. (a) These lines have a unique solution as they are intersecting at a point.
Hint: Use different algebraic methods in order to solve a pair of linear equations.
Question.7. Consider the equations shown.
4x+3y=41 and
x+3y=26
Which of these is the correct way of solving the given pair of equations?
(a) 4x-x+3y-3y=41-26
(b) 4(x+3y)+3y=41
(c) 4x+x+3y-3y=41-26
(d) 4x+3y+3y=41-26
Answer. (a) 4x-x+3y-3y=41-26
Question.8. In the equations shown below, a and b are unknown constants.
3ax+4y=-2 and
2x+by=14
If (–3, 4) is the solution of the given equations, what are the values of a and b?
(a) a=2, b=5
(b) a=-2, b=5
(c) a=5, b=2
(d) a=5, b=-2
Answer. (a) a=2, b=5
Hint: Use the most appropriate algebraic method in order to solve the given pair of linear equations.
Question.9. Consider the equations shown.
p+q=5 &
p-q=2
Which of these are the values of p and q?
(a) p=3.5, q=1.5
(b) p=1.5, q=3.5
(c) p=4, q=2
(d) p=2, q=4
Answer. (a) p=3.5, q=1.5
Question.10. Consider the equations shown:
ax+by=ab &
2ax+3by=3b
Which of these is the value of y in terms of a?
(a) y=2a-35
(b) y=2ab-3b
(c) y=9a-35
(d) y=3-2a
Answer. (d) y=3-2a
Hint: Use the concepts of pair of linear equations in two variables in order to represent any given situation algebraically and find its solution.
Question.11. Shivi gave a note of ₹2,000 for a pair of jeans worth ₹500. She was returned 11 notes in denominations of ₹200 and ₹100. Which pair of equations can be used to find the number of ₹200 notes, x, and the number of ₹100 notes x? How many notes of ₹200 did she get?
(a) x+y=11 and 200x+100y=1500; 8
(b) y=x+11 and 200x+100y=2000; 4
(c) x+y=11 and 200x+100y=1500; 4
(d) x+y=11 and 100x+200y=2000; 10
Answer. (c) x+y=11 and 200x+100y=1500; 4
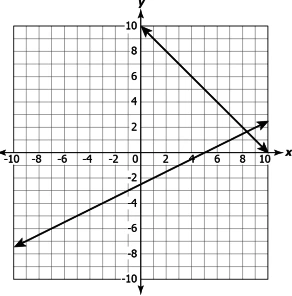
Question.12. Arnav wants to plant some saplings in columns. If he increases the number of saplings in a column by 4, the number of columns decreases by 1. If he decreases the number of saplings by 5 in a column, the number of columns increased by 2.
Which of these graphs relates the number, x, of columns and the number, y, of plants in a column?
(a) 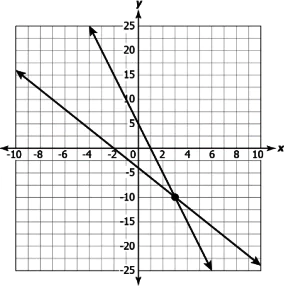
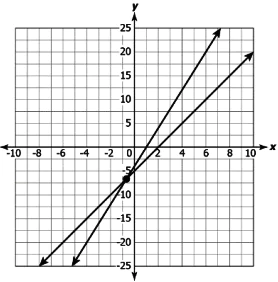
Answer. (d)
Hint: Calculate the ratio of coefficients of linear equations in order to discuss the nature of pair of linear equations.
Question.13. Consider the equations as shown:
9x+6y=5 and
3x+2y=7
Which of these is true about the given equations?
(a) This is a pair of coincident lines as \frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}=\frac{c_{1}}{c_{2}}
(b) This is a pair of Intersecting lines as \frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}
(c) This is a pair of coincident lines as \frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}
(d) This is a pair of parallel lines as \frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}
Answer. (d) This is a pair of parallel lines as \frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}\neq \frac{c_{1}}{c_{2}}
Question.14. Consider the equations as shown:
(x-a)(y-b)=(x-2a)(y-\frac{b}{2}) and
x(x+\frac{1}{2b})+y(y+\frac{a}{2})-2xy=5+(x-y)^{2}
On comparing the coefficients, a student says these pairs of equations is consistent. Is he/she correct? Which of these explains why?
(a) Yes; because they are intersecting lines.
(b) Yes; because they are parallel lines.
(c) No; because they are parallel lines.
(d) No; because they are intersecting lines.
Answer. (a) Yes; because they are intersecting lines.
Hint: Rewrite the given equations (using substitution method) which are reducible to a pair of linear equations in order to find the solution of those equations.
Question.15. Consider a pair of equations as shown.
\frac{7}{x+2}+\frac{2}{y-2}=\frac{33}{20} and
\frac{2}{x+2}+\frac{6}{y-2}=\frac{23}{20}
Which of these pair of equations is equivalent to the given pair of equations?
(a) 7u+2v=\frac{20}{33} and 2u+6v=\frac{20}{23}
(b) 7u+6v=\frac{33}{20} and 2u+2v=\frac{23}{20}
(c) 7u+2v=\frac{33}{20} and 2u+6v=\frac{23}{20}
(d) 2u+6v=\frac{33}{20} and 7u+2v=\frac{23}{20}
Answer. (c) 7u+2v=\frac{33}{20} and 2u+6v=\frac{23}{20}
Question.16. Consider a pair of equations as shown.
\frac{5}{x+2}+\frac{7}{y+2}=\frac{31}{12} and
\frac{4}{x+2}+\frac{3}{y+2}=\frac{17}{12}
What is the value of x and y ?
(a) x=2 and y=4
(b) x=4 and y=2
(c) x=14 and y=16
(d) x=16 and y=14
Answer. (b) x=4 and y=2