Competency Based Questions for Class 10 Maths Chapter 8 Introduction to Trigonometry

Competency Based Questions are new type of questions asked in CBSE Board exam for class 10. Practising the following Competency Based Questions will help the students in facing Board Questions.

Hint: Describe trigonometry in order to study the relationship between side and angle of a triangle.

Question.1. Which of the following completes the statement below?
The adjacent and ______ of right triangle depends on the angle x being referred to in that triangle and for the complementary angle (90 − 𝑥)° & of that triangle, the adjacent and opposite are ___________.

(a) opposite side, reversed
(b) opposite side, same
(c) hypotenuse, reversed
(d) hypotenuse, same

Answer. (a) opposite side, reversed

Question.2. Considering the diagram below. 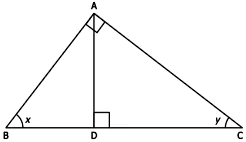Which of the following statements is true?

(a) Side AC is adjacent to \angle y in triangle ADC and triangle ABC
(b) Side AC is adjacent to \angle y in triangle ADC and side BC is adjacent to \angle y in triangle ABC
(c) Side DC is adjacent to \angle y in triangle ADC and side AC is adjacent to \angle y in triangle ABC
(d) Side AC is adjacent to \angle y in triangle ADC and side DC is adjacent to \angle y in triangle ABC

Answer. (c) Side DC is adjacent to \angle y in triangle ADC and side AC is adjacent to \angle y in triangle ABC

Hint: Define and distinguish various trigonometric ratios in order to describe and verify sine, cosine, tangent, cosecant, secant, cotangent of an angle.

Question.3. Consider the triangle shown below. 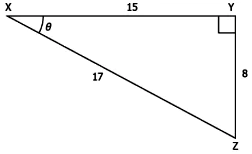What are the values of tan θ, cosec θ and sec θ?

(a) tan θ = \frac{8}{15}, cosec θ = \frac{17}{15}, sec θ = \frac{17}{8}
(b) tan θ = \frac{8}{15}, cosec θ = \frac{17}{8}, sec θ = \frac{17}{15}
(c) tan θ = \frac{17}{15}, cosec θ = \frac{8}{15}, sec θ = \frac{17}{8}
(d) tan θ = \frac{8}{15}, cosec θ = \frac{17}{15}, sec θ = \frac{8}{17}

Answer. (b) tan θ = \frac{8}{15}, cosec θ = \frac{17}{8}, sec θ = \frac{17}{15}

Question.4. Observe the figure shown. 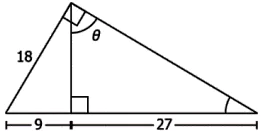Which of these is the value of cos θ?

(a) \frac{1}{2}
(b) \frac{2}{1}
(c) \frac{2 \sqrt{3}}{3}
(d) \frac{3 \sqrt{3}}{2}

Answer. (a) \frac{1}{2}

Hint: Use given trigonometric ratio(s) in order to find and verify other trigonometric ratios/angles of the triangle.

Question.5. If sin θ = \frac{7}{\sqrt{85}}, what are the values of tan θ, cos θ and cosec θ?

(a) tan θ = \frac{7}{6}, cos θ =\frac{6}{\sqrt{85}} and cosec θ = \frac{\sqrt{85}}{7}
(b) tan θ = \frac{6}{7}, cos θ =\frac{7}{\sqrt{85}} and cosec θ = \frac{\sqrt{85}}{7}
(c) tan θ = \frac{7}{6}, cos θ =\frac{7}{\sqrt{85}} and cosec θ = \frac{\sqrt{85}}{7}
(d) tan θ = \frac{6}{7}, cos θ =\frac{6}{\sqrt{85}} and cosec θ = \frac{\sqrt{85}}{6}

Answer. (a) tan θ = \frac{7}{6}, cos θ =\frac{6}{\sqrt{85}} and cosec θ = \frac{\sqrt{85}}{7}

Question.6. The two legs AB and BC of right triangle ABC are in a ratio 1:3. What will be the value of sin C?

(a) \frac{1}{\sqrt{10}}
(b) \frac{3}{\sqrt{10}}
(c) \frac{1}{3}
(d) \frac{1}{2}

Answer. (a) \frac{1}{\sqrt{10}}

Hint: Compute the trigonometric ratio of 0°, 30°, 45°, 60°, 90° in order to know and apply the value of specific angles.

Question.7. What is the value of \frac{3-sin^{2}60°}{tan 30° tan 60°}?

(a) 1 \frac{1}{4}
(b) 2 \frac{1}{4}
(c) 2 \frac{1}{2}
(d) 2 \frac{3}{4}

Answer. (b) 2 \frac{1}{4}

Question.8. The value of \frac{4-sin^{2}45°}{cot k  tan 60°} is 3.5.
What is the value of k?

(a) 30°
(b) 60°
(c) 45°
(d) 90°

Answer. (b) 60°

Hint: Compute the trigonometric ratio of complimentary angles in order to apply the values in mathematical problems.

Question.9. What is the value of \frac{5 csc 55°}{sec 35°}?

(a) \frac{5}{2}
(b) \frac{15}{2}
(c) 5
(d) 15

Answer. (b) \frac{15}{2}

Question.10. If sec 2x = \frac{1}{sin (x-36)°}, where 2x is an acute angle, what is the value of x?

(a) 36
(b) 42
(c) 48
(d) 52

Answer. (b) 42

Hint: Compute and apply trigonometric identities in order to simplify and solve mathematical problems.

Question.11. Which of these is equivalent to \frac{2 tan x (sec^{2}x-1)}{cos^{3}x}?

(a) 2 tan^{3}x csc x
(b) 2 tan^{3}x sec^{3} x
(c) 2 tan^{3}x csc^{3} x
(d) 2 cot^{3}x sec^{3} x

Answer. (b) 2 tan^{3}x sec^{3} x

Question.12. Which of the following option makes the statement below true?
\frac{\frac{1}{sec x}+sec x}{cos^{2}x-1-tan^{2}x} = ?

(a) −cosec x cot x
(b) − sec x cot x
(c) −cosec x tan x
(d) − sec x tan x

Answer. (a) −cosec x cot x