Competency Based Questions Chapter 4 Linear Equations in Two Variables
Chapter 4: Linear Equations in Two Variables focuses on competency-based questions to enhance your mathematical proficiency. Delve into practical exercises, detailed solutions, and insightful explanations designed to solidify your understanding and improve your problem-solving skills. Ideal for students and educators aiming for a comprehensive learning experience.
Hint: Recall concepts of coefficients and variables in order to construct a linear equation from a given statement.
Question.1. In an exhibition, the cost of tickets for an adult is ₹5 more than thrice the cost of ticket for a child. Which equation relates the cost, y, of adult ticket in terms of the cost, x, of child ticket?
(a) y=5+3x
(b) y+5=3x
(c) y=3+5x
(d) y+3=5x
Question.2. Ravi is a salesperson and earns a fixed salary per month plus a commission on his monthly sales. Ravi’s monthly earnings is given by the equation y=10,000+0.05x. Ravi gets a hike of 10% on his fixed salary and will now be earning ₹140 on every 2000 rupees worth of sales. Which equation shows Ravi’s monthly earnings after the hike?
(a) y=11,000+0.14x
(b) y=11,000+0.07x
(c) y=12,000+0.10x
(d) y=12,000+0.15x
Ans.1. (a) y=5+3x
Ans.2. (b) y=11,000+0.07x
Hint: Compare a given linear equation to the standard form ax+by+c=0 in order to deduce the values of a, b and c.
Question.3. Which option shows 5y-8x=7(x+y)-9 expressed in the form of ax+by+c=0?
(a) -x+6y-9=0
(b) -x+12y-9=0
(c) 15x+2y-9=0
(d) 15x-4y-9=0
Question.4. In the equation shown, k>0, -(k+1)x+ky-5k=1-2ky. The equation when expressed in the form ax+by+c=0 gives c=6. What are the values of a and b?
(a) a=2 and b=-3
(b) a=-2 and b=3
(c) a=-2 and b=-1
(d) a=2 and b=1
Ans.3. (c) 15x+2y-9=0
Ans.4. (a) a=2 and b=-3
Hint: Use substitution method in order to deduce whether the ordered pair is solution to a given linear equation.
Question.5. Which of these equations has (1.5, 4) as one of the solutions?
(a) 20x+5y=87.5
(b) 20x+5y=50
(c) 20x+5y=520
(d) 20x+5y=270
Question.6. Rahul claims that (4, 3) is one of the solutions of the equation 2x-y+3=5. Is Rahul’s claim correct?
(a) Yes, as 2(4 − 3) + 3 simplifies to 5 and 5 is also the number on the right-hand side of the equation.
(b) Yes, as 2(3) − 4 + 3 simplifies to 5 and 5 is also the number on the right-hand side of the equation.
(c) No, but replacing 5 in the given equation with 8 will result in the equation having (4, 3) as one of its solutions.
(d) No, but replacing 5 in the given equation with 3 will result in the equation having (4, 3) as one of its solutions.
Ans.5. (b) 20x+5y=50
Ans.6. (c) No, but replacing 5 in the given equation with 8 will result in the equation having (4, 3) as one of its solutions.
Hint: Solve an equation in order to represent it on a number line and a Cartesian plane.
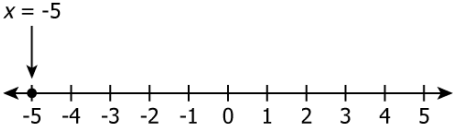
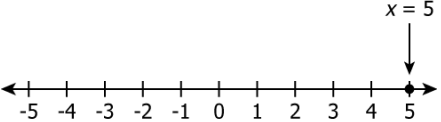
Question.7. Which number line shows the solution of the equation 3(x-3)+2(x+1)=8?
(a) 
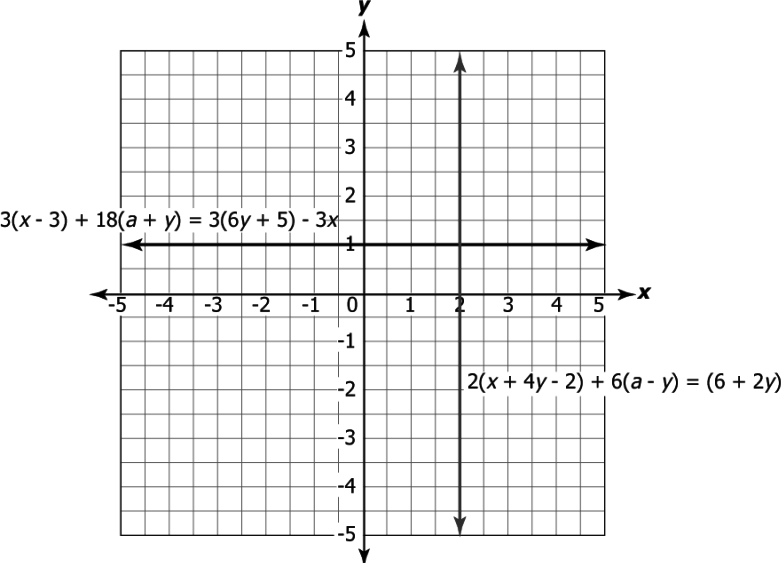
Question.8. Consider the equations.
Equation 1: 2(x+4y-2)+6(a-y)=(6+2y)
Equation 2: 3(x-3)+18(a+y)=3(6y+5)-3x
Which of these represents the graph of the above equations?
(a) 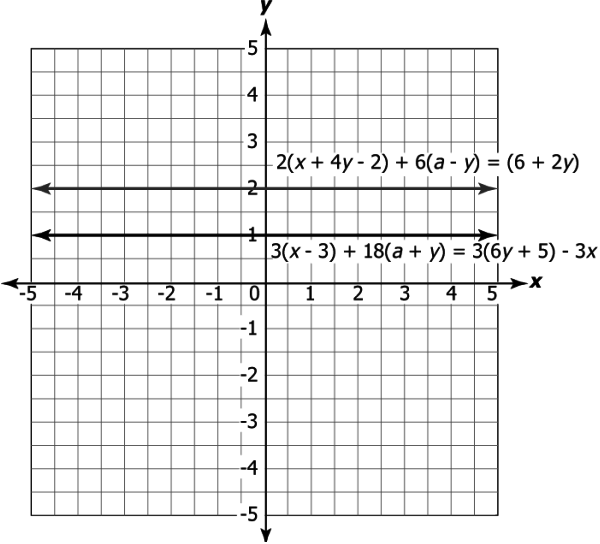
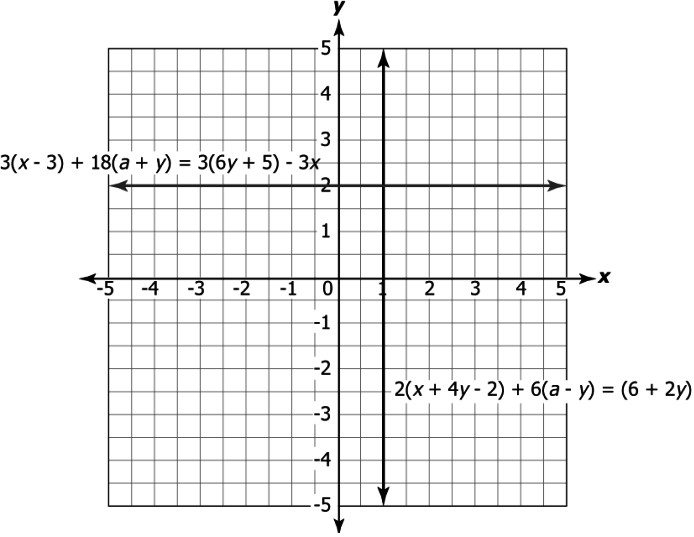
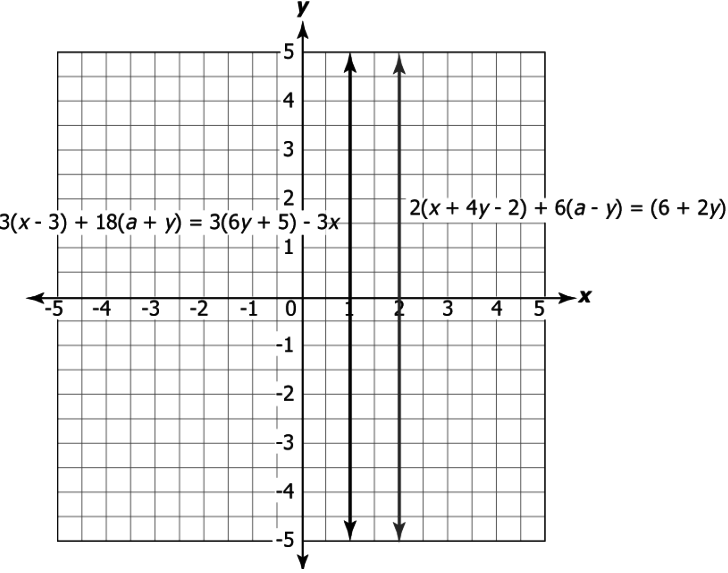
Ans.7. (a)
Ans.8. (c)
Hint: Apply principles of linear equations in order to formulate and solve for a variety of problems in real life situations.
Question.9. A person invested money in an account and earns interest of ₹100 every month. Which equation shows the total interest, y, the person will earn after x months and how much interest will the person earn in 1 year?
(a) y=12x; 144
(b) y=12x+100; 154
(c) y=100x; 120
(d) y=100x; 1200
Question.10. A swimming academy charges onetime registration fees plus fixed monthly fee. Mayank joined the academy and paid ₹1200 in the first month including registration fee and ₹700 in the second month. Which linear equation shows the total fee, y, for x months and the total fee for 6 months?
(a) y=1200+700x; 5400
(b) y=1200+700x; 4700
(c) y=500+700x; 4700
(d) y=500+700x; 5400
Ans.9. (d) y=100x; 1200
Ans.10. (c) y=500+700x; 4700