Competency Based Questions
CBSE CBSE Class 9 Mathematics Class 9 Competency Based Questions

Competency Based Questions Chapter 7 Triangles

Unlock the potential of “Competency Based Questions for Chapter 7: Triangles” with our comprehensive guide! This blog provides detailed explanations, practical tips, and structured solutions to help you excel in solving competency-based questions in geometry. Enhance your analytical and problem-solving skills with our expert insights and real-world examples. Perfect for students and educators alike, our guide simplifies complex concepts, making learning effective and enjoyable.

Ready to master Chapter 7 Triangles? Explore our guide now!

Hint: Observe the angles and sides of the given figures in order to show that they are congruent or not congruent.

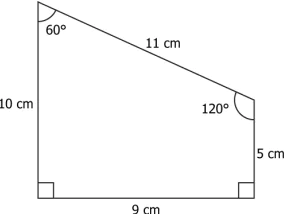
Question.1. A figure is shown.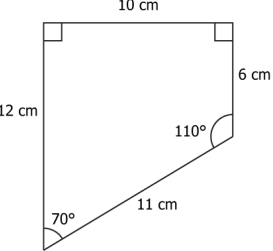cbe-questions-ma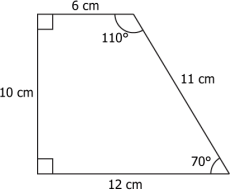ths-class-9-ch-7-q-1Which of these figures is congruent to the given figure?

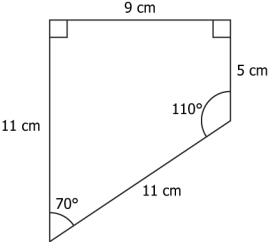
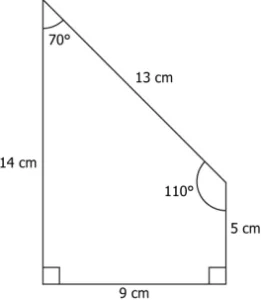
(a) cbe-questions-maths-class-9-ch-7-q-1-a(b) cbe-questions-maths-class-9-ch-7-q-1-b(c) cbe-questions-maths-class-9-ch-7-q-1-c(d) cbe-questions-maths-class-9-ch-7-q-1-d

Question.2. Consider the following two statements about the rectangles a student draws.
Statement 1: Rectangles have the same perimeter.
Statement 2: Rectangles have the same area.
Which of the following statements is sufficient to conclude that the rectangles are congruent?

(a) Statement 1 alone is sufficient, but statement 2 alone is not sufficient.
(b) Statement 2 alone is sufficient, but statement 1 alone is not sufficient.
(c) Both statements together are sufficient, but neither statement alone is sufficient.
(d) Both statements together are not sufficient.

Ans.1. (a) cbe-questions-maths-class-9-ch-7-q-1-aAns.2. (c) Both statements together are sufficient, but neither statement alone is sufficient.

Hint: Apply concepts of linear pairs of angles, vertically opposite angles, corresponding angles, alternate angles, transversal angles & exterior angles of a triangle in order to prove congruence between 2 triangles in a given figure.

Question.3. Consider the triangles made by two intersecting lines as shown.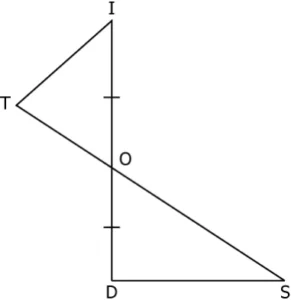cbe-questions-maths-class-9-ch-7-q-3What additional information is required to prove that ∆TOI ≅ ∆SOD?

(a) \angleDOS = \angleTOI
(b) \angleOTI = \angleODI
(c) TO = OS
(d) TI = DS

Question.4. Consider the parallelogram as shown.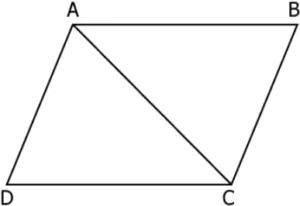cbe-questions-maths-class-9-ch-7-q-4Based on the given information, can it be concluded that ∆DAC ≅ ∆ BCA? Why or why not?

(a) Yes, because AB = CD, AD = BC, \angleDAC = \angleACB, \angleDCA = \angleCAB, \angleADC = \angleABC and AC = AC.
(b) Yes, because AB = CD, AD = BC, \angleDAC = \angleCAB, \angleDCA = \angleACB, \angleADC = \angleABC and AC = AC.
(c) No, because angle measures are not known.
(d) No, because side lengths are not known.

Ans.3. (c) TO = OS
Ans.4. (a) Yes, because AB = CD, AD = BC, \angleDAC = \angleACB, \angleDCA = \angleCAB, \angleADC = \angleABC and AC = AC.

Hint: Illustrate the criterions of congruencies of triangles through diagrams (ASA, SAS, SSS. RHS) in order to prove relationships between given angles, sides and triangles of a given figure.

Question.5. Consider the triangles shown.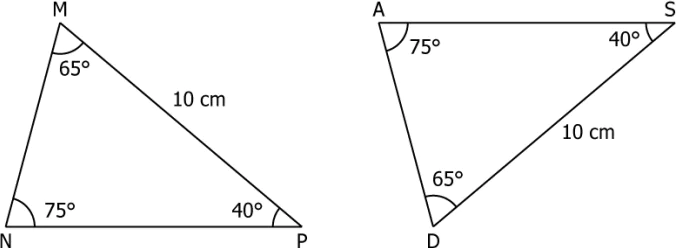cbe-questions-maths-class-9-ch-7-q-5Which congruency criteria can be used to show that triangles are congruent?

(a) SSS
(b) SAS
(c) AAA
(d) ASA

Question.6. Consider the triangles shown.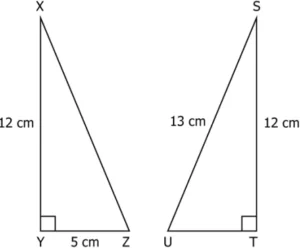cbe-questions-maths-class-9-ch-7-q-6Which of these is not true about the given triangles?

(a) ∆XYZ ≅ ∆STU (by SSS congruence rule).
(b) ∆XYZ ≅ ∆STU (by RHS congruence rule).
(c) ∆XYZ ≅ ∆STU (by ASA congruence rule).
(d) ∆XYZ ≅ ∆STU (by SAS congruence rule).

Ans.5. (d) ASA
Ans.6. (c) ∆XYZ ≅ ∆STU (by ASA congruence rule).

Hint: Apply criterions for congruence in a triangle with two congruent sides in order to prove that the angle opposite to the sides are equal and apply it in a given figure to solve for the measure of an angle.

Question.7. In triangle ZAT, AZ = AT and AE bisects \angleZAT.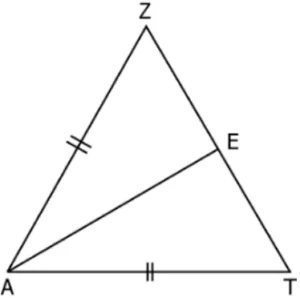cbe-questions-maths-class-9-ch-7-q-7If the measure of \angleZAT is 50°, which angle measures 25°?

(a) \angleZAE
(b) \angleZTA
(c) \angleAET
(d) \angleAEZ

Question.8. In the triangle below, AD is the bisector of \angleA and AB = AC.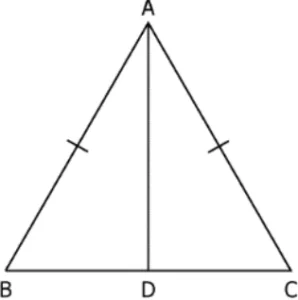cbe-questions-maths-class-9-ch-7-q-8Which option has words that correctly complete the statement below?
By _____ congruency criteria, ∆ABD ≅ ∆ACD and using CPCTC, we get \angleABC = ____.

(a) ASA; \angleACD
(b) SAS; \angleACD
(c) ASA; \angleADC
(d) SAS; \angleADC

Ans.7. (a) \angleZAE
Ans.8. (b) SAS; \angleACD

Hint: Examine given triangles that satisfy AAA or SSA criteria in order to comment whether they are congruent.

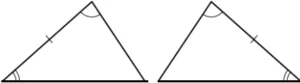
Question.9. Which of these pairs of triangles are not congruent?

(a) 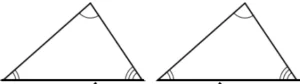cbe-questions-maths-class-9-ch-7-q-9-a(b) cbe-questions-maths-class-9-ch-7-q-9-b(c) cbe-questions-maths-class-9-ch-7-q-9-c(d) cbe-questions-maths-class-9-ch-7-q-9-d

Question.10. Two triangles are shown. 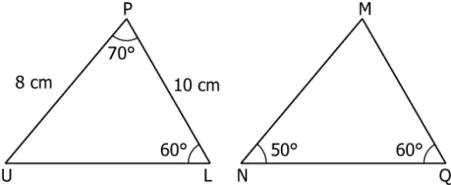cbe-questions-maths-class-9-ch-7-q-10The perimeter of ∆PUL is 30 cm. Are the triangles congruent?

(a) Yes, as on calculating the missing angle in each triangle it can be concluded that the triangles are congruent by AAA criteria.
(b) No, as the missing angle in each triangle cannot be calculated.
(c) Conclusion about the congruency of triangles can be made provided the length of the side NQ of triangle MNQ is known.
(d) Conclusion about the congruency of triangles can be made provided the length of the side MN or side MQ of triangle MNQ is known.

Ans.9. (a) cbe-questions-maths-class-9-ch-7-q-9-aAns.10. (d) Conclusion about the congruency of triangles can be made provided the length of the side MN or side MQ of triangle MNQ is known.

Hint: Using properties of triangles prove the relationship between any given sides or angles in a given figure.

Question.11. In the given triangle, LN = MN.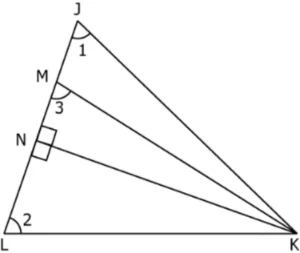cbe-questions-maths-class-9-ch-7-q-11If JK = 13 cm, which could be the length of LK?

(a) 9 cm
(b) 13 cm
(c) 17 cm
(d) 26 cm

Ans.11. (a) 9 cm

Tagged In

Related Posts

Leave a Reply

Your email address will not be published. Required fields are marked *

You cannot copy content of this page