What is Case Study Question / Paragraph Based Question?
A case study is a scenario in a particular academic / professional context which students are expected to analyse and respond to, guided by specific questions posed concerning the situation. In many cases, the scenario or case study involves a number of issues or problems that must be dealt with in a academic / professional workplace.
Why Case Study Questions are included in academics?
Case study assignments usually require students to identify problems and issues in a scenario, to demonstrate their developing knowledge of theories and academic / professional policies and to make decisions and recommendations based on these to either prevent or solve some of the issues in that scenario.
How to solve Case Study Questions?
There are several steps to writing an answer to a case study assignment:
STEP 1: Read the case study and questions carefully.
- Read the case and associated questions carefully.
- Highlight the main points of the case and any issues that you can identify.
- Read the questions closely and analyse what they are requiring you to do.
- Read the case again, linking the information that is relevant to each question you have been asked.
STEP 2: Identify the issues in the case study.
Case studies describe a situation which may arise in a particular profession or social context. They often involve a number of people in a complex situation. They will often describe a situation which is problematic, possibly in how it is dealt with, or in its complexity. An important part of your answer is to analyse the situation and to identify the issues/actions described in the case which may be problematic. The following questions may help you to do this:
- What actions were taken in the case?
- Were these actions the most appropriate and why?
- Were there any consequences of the actions taken?
- Was anything omitted or not considered?
- Were actions/procedures in line with existing codes of practice, policy or theories?
STEP 3: Link theory to practice.
Use your knowledge of existing codes of practice, theories and/or other academic / professional documents and behaviours to decide what was done appropriately and what was not.
STEP 4: Plan your answer.
It can be useful to use the questions you have been set as headings and to answer each part in turn, reducing the chance of omitting set questions. You can always take out the headings before you submit if you wish. Lecturers usually set questions in a logical order, so answer in the order they are written in your question.
STEP 5: Start writing your case study answer (for theory only)
Like any assignment, you will need an introduction, body sections in which you answer the questions put to you regarding the case study, and a conclusion.
STEP 6: Edit and proofread.
Read through your paper yourself to detect and correct other errors and omissions.
Check you have answered all questions and backed up your answer with relevant passage.
Types of Case Study Questions / Paragraph Based Questions
Case Study Questions / Paragraph Based Questions can be broadly classified into two types:
- MCQs type: In this type, student has to tick the correct option from various options.
- Theory type: In this type, student has to write proper solution / answer in cotext to the case study.
Case Study/ Passage Based Questions Chapter 1 Real numbers Mathematics
Type 1: MCQ type
Case Study Question 01
Read the following and answer any four questions from 1 to 4 given below:
In a classroom activity on real numbers, the students have to pick a number card from a pile and frame question on it if it is not a rational number for the rest of the class. The number cards picked up by first 5 students and their questions on the numbers for the rest of the class are as shown below. Answer them.
Question.1. Suraj picked up \sqrt{8} and his question was – Which of the following is true about \sqrt{8} ?
(a) It is a natural number
(b) It is an irrational number
(c) It is a rational number
(d) None of these
Question.2. Shreya picked up ‘BONUS’ and her question was – Which of the following is not irrational?
(a) 3-4\sqrt{5}
(b) \sqrt{7} -6
(c) 2+2\sqrt{9}
(d) 4\sqrt{11} -6
Question.3. Ananya picked up \sqrt{15}-\sqrt{10} and her question was – \sqrt{15}-\sqrt{10} is __________ number.
(a) a natural
(b) an irrational
(c) a whole
(d) a rational
Question.4. Suman picked up \frac{1}{\sqrt{5}} and her question was – \frac{1}{\sqrt{5}} is ____________ number.
(a) a whole
(b) a rational
(c) an irrational
(d) a natural
Question.5. Preethi picked up \sqrt{6} and her question was – Which of the following is not irrational?
(a) 15+3\sqrt{6}
(b) \sqrt{24}-9
(c) 5\sqrt{150}
(d) None of these
Ans.1. (b)
Here \sqrt{8} = 2\sqrt{2}= product of rational and irrational numbers = irrational number
Ans.2. (c)
Here, \sqrt{9} = 3
So, 2+2\sqrt{9}= 2 + 6 = 8, which is not irrational.
Ans.3. (b)
Here \sqrt{15} and \sqrt{10} are both irrational and difference of two irrational numbers is also irrational.
Ans.4. (c)
As \sqrt{5} is irrational, so its reciprocal is also irrational.
Ans.5. (d)
We know that \sqrt{6} is irrational. So, 15+3\sqrt{6} is irrational.
Similarly, \sqrt{24}-9 = 2\sqrt{6}-9 is irrational.
And 5\sqrt{150} = 5 \times 5\sqrt{6} = 25\sqrt{6} is irrational.
Case Study Question 02
Read the following and answer any four questions from 1 to 5 given below:
Decimal form of rational numbers can be classified into two types.
- Let x be a rational number whose decimal expansion terminates. Then x can be expressed in the form \frac{p}{q} , where p and q are co-prime and the prime factorisation of q is of the form 2^{n}\cdot 5^{m} , where n , m are non- negative integers and vice-versa.
- Let x= \frac{p}{q} be a rational number, such that the prime factorisation of q is not of the form 2^{n}\cdot 5^{m} , where n and m are non-negative integers. Then x has a non-terminating repeating decimal expansion.
Question.1. Which of the following rational numbers have a terminating decimal expansion?
(a) \frac{125}{441}
(b) \frac{77}{210}
(c) \frac{15}{1600}
(d) \frac{129}{(2^{2}\times 5^{2} \times 7^{2})}
Question.2. \frac{23}{(2^{3}\times 5^{2})} =
(a) 0.575
(b) 0.115
(c) 0.92
(d) 1.15
Question.3. \frac{441}{(2^{2}\times 5^{7} \times 7^{2})} is a _________
decimal.
(a) terminating
(b) recurring
(c) non-terminating and non-recurring
(d) None of these
Question.4. For which of the following value(s) of p , \frac{251}{(2^{3}\times p^{2})} is a non-terminating recurring decimal?
(a) 3
(b) 7
(c) 15
(d) All of these
Question.5. \frac{241}{(2^{5}\times 5^{3})} is a _________ decimal.
(a) terminating
(b) recurring
(c) non-terminating and non-recurring
(d) None of these
Ans.1. (c)
Here, the simplest form of given options are
\frac{125}{441} = \frac{5^{3}}{3^{2}\times 7^{2}},
\frac{77}{210} = \frac{11}{2 \times 3\times 5},
\frac{15}{1600} = \frac{3}{2^{6} \times 5},
Out of all the given options, the denominator of option (c) alone has only 2 and 5 as factors. So, it is a terminating decimal.
Ans.2. (b)
\frac{23}{2^{3}\times 5^{2}} = \frac{23}{200} = 0.115
Ans.3. (a)
\frac{441}{2^{2}\times 5^{7}\times 7^{2}} = \frac{9}{2^{2}\times 5^{7}}, which is a terminating decimal.
Ans.4. (d)
The fraction form of a non-terminating recurring decimal will have at least one prime number other than 2 and 5 as its factors in denominator. So, p can take either of 3, 7 or 15.
Ans.5. (a)
Here denominator has only two prime factors i.e., 2 and 5 and hence it is a terminating decimal.
Case Study Question 03
Read the following and answer any four questions from 1 to 5 given below:
HCF and LCM are widely used in number system especially in real numbers in finding relationship between different numbers and their general forms. Also, product of two positive integers is equal to the product of their HCF and LCM.
Based on the above information answer the following questions.
Question.1. If two positive integers x and y are expressible in terms of primes as x=p^{2}q^{3} and y=p^{3}q , then which of the following is true?
(a) HCF=pq^{2}\times LCM
(b) LCM=pq^{2}\times HCF
(c) LCM=p^{2}q \times HCF
(d) HCF=p^{2}q \times LCM
Question.2. A boy with collection of marbles realizes that if he makes a group of 5 or 6 marbles, there are always two marbles left, then which of the following is correct if the number of marbles is p?
(a) p is odd
(b) p is even
(c) p is not prime
(d) both (b) and (c)
Question.3. Find the largest possible positive integer that will divide 398, 436 and 542 leaving remainder 7, 11, 15 respectively.
(a) 3
(b) 1
(c) 34
(d) 17
Question.4. Find the least positive integer which on adding 1 is exactly divisible by 126 and 600.
(a) 12600
(b) 12599
(c) 12601
(d) 12500
Question.5. If A, B and C are three rational numbers such that 85C – 340A = 109, 425A + 85B = 146, then the sum of A, B and C is divisible by
(a) 3
(b) 6
(c) 7
(d) 9
Ans.1. (b)
LCM of x and y=p^{3}\times q^{3} and HCF of x and y=p^{2}\times q
Also, LCM=pq^{2} \times HCF .
Ans.2. (d)
Number of marbles = 5m+2 or 6n+2 .
Thus, number of marbles, p=(multiple of 5 \times 6)+2 p
= 30k+2
= 2(15k+1)
= which is an even number but not prime.
Ans.3. (d)
Here, required numbers
= HCF (398-7, 436-11, 542-15)
= HCF (391, 425, 527) = 17
Ans.4. (b)
LCM of 126 and 600 = 2\times 3\times 21\times 100 = 12600.
The least positive integer which on adding 1 is exactly divisible by 126 and 600 = 1260-1 = 12599
Ans.5. (a)
Here, 85C-340A = 109 and 425A + 85B = 146
On adding them, we get
85A + 85B + 85C = 255
⇒ A+B+C = 3, which is divisible by 3.
Case Study Question 04
Read the following and answer any four questions from 1 to 5 given below:
Srikanth has made a project on real numbers, where he finely explained the applicability of exponential laws and divisibility conditions on real numbers. He also included some assessment questions at the end of his project as listed below. Answer them.
Question.1. For what value of n , 4^{n} ends in 0?
(a) 10
(b) when n is even
(c) when n is odd
(d) no value of n
Question.2. If a is a positive rational number and n is a positive integer greater than 1, then for what value of n , a^{n} is a rational number?
(a) when n is any even integer
(c) for all n>1
(b) when n is any odd integer
(d) only when n=0
Question.3. If x and y are two odd positive integers, then which of the following is true?
(a) x^{2}+y^{2} is even
(b) x^{2}+y^{2} is not divisible by 4
(c) x^{2}+y^{2} is odd
(d) both (a) and (b)
Question.4. The statement ‘One of every three consecutive positive integers is divisible by 3’ is
(a) always true
(b) always false
(c) sometimes true
(d) None of these
Question.5. If n is any odd integer, then n^{2}-1 is divisible by
(a) 22
(b) 55
(c) 88
(d) 8
Ans.1. (d)
For a number to end in zero it must be divisible by 5, but 4^{n}=2^{2n} is never divisible by 5. So, 4^{n} never ends in zero for any value of n .
Ans.2. (c)
We know that product of two rational numbers is also a rational number.
So, a^{2}=a \times a = rational number
a^{3}=a^{2} \times a = rational number
a^{4}=a^{3} \times a = rational number
………………………
………………………
a^{n}=a^{n-1} \times a = rational number.
Ans.3. (d)
Let x=2m+1 and y=2k+1
Then x^{2}+y^{2}= (2m+1)^{2}+(2k+1)^{2}
= 4m^{2}+4m+1+4k^{2}+4k+1
= 4(m^{2}+k^{2}+m+k)+2
So, it is even but not divisible by 4.
Ans.4. (a)
Let three consecutive positive integers be n , n+1 and n+2 .
We know that when a number is divided by 3, the remainder obtained is either 0 or 1 or 2.
So, n=3p or 3p+1 or 3p+2 , where p is some integer.
If n=3p , then n is divisible by 3.
If n=3p+1 , then n+2=3p+1+2=3p+3=3(p+1) is divisible by 3.
If n=3p+2 , then n+1=3p+2+1=3p+3=3(p+1) is divisible by 3.
So, we can say that one of the numbers among n , n+1 and n+2 is always divisible by 3.
Ans.5. (d)
Any odd number is of the form of (2k+1) , where k is any integer.
So, n^{2}-1=(2k+1)^{2}-1=4k^{2}+4k
For k=1 , 4k^{2}+4k=8 , which is divisible by 8. Similarly, for k=2 , 4k^{2}+4k=24 , which is divisible by 8.
And for k=3 , 4k^{2}+4k=48 , which is also divisible by 8.
So, 4k^{2}+4k is divisible by 8 for all integers k , i.e., n^{2}-1 is divisible by 8 for all odd values of n .
Case Study Question 05
Read the following and answer any four questions from 1 to 5 given below:
Real numbers are extremely useful in everyday life. That is probably one of the main reasons we all learn how to count and add and subtract from a very young age. Real numbers help us to count and to measure out quantities of different items in various fields like retail, buying, catering, publishing etc. Every normal person uses real numbers in his daily life. After knowing the importance of real numbers, try and improve your knowledge about them by answering the following questions on real life based situations.
Question.1. Three people go for a morning walk together from the same place. Their steps measure 80 cm, 85 cm and 90 cm respectively. What is the minimum distance travelled when they meet at first time after starting the walk assuming that their walking speed is same?
(a) 6120 cm
(b) 12240 cm
(c) 4080 cm
(d) None of these
Question.2. In a school Independence Day parade, a group of 594 students need to march behind a band of 189 members. The two groups have to march in the same number of columns. What is the maximum number of columns in which they can march?
(a) 9
(b) 6
(c) 27
(d) 29
Question.3. Two tankers contain 768 litres and 420 litres of fuel respectively. Find the maximum capacity of the container which can measure the fuel of either tanker exactly.
(a) 4 litres
(b) 7 litres
(c) 12 litres
(d) 18 litres
Question.4. The dimensions of a room are 8 m 25 cm, 6 m 75 cm and 4 m 50 cm. Find the length of the largest measuring rod which can measure the dimensions of room exactly.
(a) 1 m 25 cm
(b) 75 cm
(c) 90 cm
(d) 1 m 35 cm
Question.5. Pens are sold in pack of 8 and notepads are sold in pack of 12. Find the least number of pack of each type that one should buy so that there are equal number of pens and notepads.
(a) 3 and 2
(b) 2 and 5
(c) 3 and 4
(d) 4 and 5
Ans.1. (b)
Here 80=2^{4}\times 5 , 85=17\times 5 and 90=2\times 3^{2} \times 5
L.C.M of 80, 85 and 90 = 2^{4} \times 3^{2} \times 5 \times 17 = 12240
Hence, the minimum distance each should walk when they at first time is 12240 cm.
Ans.2. (c)
Here 594= 2 \times 3^{3} \times 11 and 189= 3^{3} \times 7
HCF of 594 and 189 = 3^{3} = 27
Hence, the maximum number of columns in which they can march is 27.
Ans.3. (c)
Here 768= 2^{8} \times 3 and 420 = 2^{2}\times 3\times 5\times 7
HCF of 768 and 420 = 2^{2} \times 3 = 12
So, the container which can measure fuel of either tanker exactly must be of 12 litres.
Ans.4. (b)
Here, Length = 825 cm, Breadth = 675 cm and Height = 450 cm
Also, 825 = 5^{2}\times 3\times 11, 675 = 3^{3}\times 5^{2} and 450 = 2\times 3^{2}\times 5^{2}
HCF = 3 \times 5 \times 5=75
Therefore, the length of the longest rod which can measure the three dimensions of the room exactly is 75 cm.
Ans.5. (a)
LCM of 8 and 12 is 24.
Therefore, The least number of pack of pens = \frac{24}{8} = 3
Also. The least number of pack of note pads = \frac{24}{12} = 2
Case Study Question 06
Read the following and answer any four questions from 1 to 5 given below:
To enhance the reading skills of grade X students, the school nominates you and two of your friends to set up a class library. There are two sections-section A and section B of grade X. There are 32 students in section A and 36 students in section B.
Question.1. What is the minimum number of books you will acquire for the class library, so that they can be distributed equally among students of Section A or Section B?
(a) 144
(b) 128
(c) 288
(d) 272
Question.2. If the product of two positive integers is equal to the product of their HCF and LCM is true then, the HCF (32, 36) is
(a) 2
(b) 4
(c) 6
(d) 8
Question.3. 36 can be expressed as a product of its primes as
(a) 2^{2}\times 3^{2}
(b) 2^{1}\times 3^{3}
(c) 2^{3}\times 3^{1}
(d) 2^{0}\times 3^{0}
Question.4. 7\times 11\times 13\times 15+15 is a
(a) Prime number
(b) Composite number
(c) Neither prime nor composite
(d) None of the above
Question.5. If p and q are positive integers such that p=ab^{2} and q=a^{2}b , where a, b are prime numbers, then the LCM (p, q) is
(a) ab
(b) a^{2}b^{2}
(c) a^{3}b^{2}
(d) a^{3}b^{3}
Ans.1. (c)
For getting least number of books, taking LCM of 32, 36
Ans.2. (b)
HCF of 32, 36 is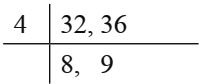
Ans.3. (a)
36 is expressed as prime
36 = 2\times 2\times 3\times 3 = 2^{2}\times 3^{2}
Ans.4. (b)
7\times 11\times 13\times 15+15
⇒ 15(7\times 11\times 13+1)
so given no. is a composite number.
Ans.5. (b) Given a, b are prime number. So
LCM of p, q, where p=ab^{2} , q=a^{2}b
p = a\times b\times b
q = a\times b\times a
a\times b\times a\times b
⇒ a^{2}\times b^{2}
Case Study Question 07
Read the following and answer any four questions from 1 to 5 given below:
A seminar is being conducted by an Educational Organisation, where the participants will be educators of different subjects. The number of participants in Hindi, English and Mathematics are 60, 84 and 108 respectively.
Question.1. In each room the same number of participants are to be seated and all of them being in the same subject, hence maximum number participants that can accommodated in each room are
(a) 14
(b) 12
(c) 16
(d) 18
Question.2. What is the minimum number of rooms required during the event?
(a) 11
(b) 31
(c) 41
(d) 21
Question.3. The LCM of 60, 84 and 108 is
(a) 3780
(b) 3680
(c) 4780
(d) 4680
Question.4. The product of HCF and LCM of 60, 84 and 108 is
(a) 55360
(b) 35360
(c) 45500
(d) 45360
Question.5. 108 can be expressed as a product of its primes as
(a) 2^{3}\times 3^{2}
(b) 2^{3}\times 3^{3}
(c) 2^{2}\times 3^{2}
(d) 2^{2}\times 3^{3}
Ans.1. (b)
For maximum number of participants, taking HCF of 60, 84 and 108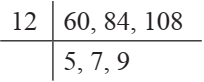
Ans.2. (d)
Minimum number of rooms required are
5 + 7 + 9 = 21
Ans.3. (a)
LCM of 60, 84, 108 is
12\times 5\times 7\times 9 = 3780
Ans.4. (d)
Product is = 12 × 3780 = 45360
Ans.5. (d)
108 = 2\times 2\times 3\times 3\times 3 = 2^{2}\times 3^{3}
Case Study Question 08
Read the following and answer any four questions from 1 to 5 given below:
A Mathematics exhibition is being conducted in your school and one of your friends is making a model of a factor tree. He has some difficulty and asks for your help in completing a quiz for the audience.
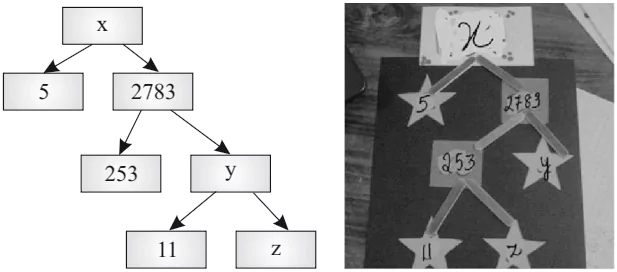
Observe the following factor tree and answer the following:
Question.1. What will be the value of x ?
(a) 15005
(b) 13915
(c) 56920
(d) 17429
Question.2. What will be the value of y ?
(a) 23
(b) 22
(c) 11
(d) 19
Question.3. What will be the value of z ?
(a) 22
(b) 23
(c) 17
(d) 19
Question.4. According to Fundamental Theorem of Arithmetic 13915 is a
(a) Composite number
(b) Prime number
(c) Neither prime nor composite
(d) Even number
Question.5. The prime factorisation of 13915 is
(a) 5\times 11^{3}\times 13^{2}
(b) 5\times 11^{3}\times 23^{2}
(c) 5\times 11^{2}\times 23
(d) 5\times 11^{2}\times 13^{2}
Ans.1. (b)
x=5\times 2783 = 13915
Ans.2. (c)
y = 253)2783( = 11
Ans.3. (b)
z = 11)253( = 23
Ans.4. (a)
Composite number having more than 2 factors.
Ans.5. (c)
Prime factorisation of 13915 =
⇒ 5\times 11^{2}\times 23
Case Study Question 09
Read the following and answer any four questions from 1 to 4 given below:
105 goats,140 donkeys and 175 cows have to be taken across a river. There is only one boat which will have to make many trips in order to do so. The lazy boatman has his own conditions for transporting them. He insists that he will take the same number of animals in every trip and they have to be of same kind. He will naturally like to take the largest possible number each time.
Question.1. How many animals have been taken in each trip?
(a) 12
(b) 35
(c) 70
(d) 24
Question.2. How many trips to be done so that all animals crossed the river?
(a) 12
(b) 35
(c) 70
(d) 24
Question.3. When the animals were doubled, how many animals could be taken in each trip?
(a) 12
(b) 35
(c) 70
(d) 24
Question.4. The LCM of all animals is
(a) 2400
(b) 2300
(c) 2100
(d) 2000
Ans.1. (b)
35
Ans.2. (a)
12
Ans.3. (c)
70
Ans.4. (c)
2100
Case Study Question 10
Read the following and answer any four questions from 1 to 5 given below:
Three sets of English, Hindi and Mathematics books have to be stacked in such a way that all the books are stored topic-wise and the height of each stack is same. The number of English books is 96,the number of Hindi books is 240 and the number of Mathematics books is 336. Assuming that the books are of the same thickness. Using this data answer the following questions
Question.1. The maximum number of books in each stack is
(a) 12
(b) 24
(c) 48
(d) 36
Question.2. Number of stacks of English books is
(a) 2
(b) 7
(c) 5
(d) 12
Question.3. Number of stacks of Mathematics books is
(a) 2
(b) 7
(c) 5
(d) 12
Question.4. Number of stacks of Hindi books is
(a) 2
(b) 7
(c) 5
(d) 12
Question.5. Which Mathematical concept was used in finding the maximum number of books in each stack?
(a) LCM
(b) HCF
(c) Neither HCF nor LCM
(d) Fundamental theorem of Arithmetic
Ans.1. (c)
48
Ans.2. (a)
2
Ans.3. (b)
7
Ans.4. (c)
5
Ans.5. (b)
HCF
Case Study Question 11
Read the following and answer any four questions from 1 to 4 given below:
Klick has a camera that takes film that allows 24 exposures,whereas Snapp has a camera that takes film that allows 36 exposures.Both of them want to be able to to take the same number of photographs and complete their rolls of film.
Question.1. Minimum number of exposures that should be taken by each
(a) 24
(b) 36
(c) 72
(d) 12
Question.2. Number of rolls Klick should buy
(a) 6
(b) 3
(c) 2
(d) 12
Question.3. Number of rolls Snapp should buy
(a) 6
(b) 3
(c) 2
(d) 12
Question.4. Which Mathematical concept was used in finding minimum number of exposures taken by each
(a) HCF
(b) LCM
(c) Neither HCF nor LCM
(d) Fundamental theorem of Arithmetic
Ans.1. (c)
72
Ans.2. (b)
3
Ans.3. (c)
2
Ans.4. (b)
LCM
Case Study Question 12
Read the following and answer any four questions from 1 to 5 given below:
For 73th republic day Parade on 26th January in Delhi, Captain RS Meel is planning for parade of following two groups:
- I. First group of Army contingent of 624 members behind an army band of 32 members.
- II. Second group of CRPF troops with 468 soldiers behind the 228 members of bikers.
These two groups are to march in the same number of columns. This sequence of soldiers is followed by jhankis of difference states which are showing the culture of the respective states.
Question.1. What is the maximum number of columns in which the army troops can march?
(a) 8
(b) 16
(c) 4
(d) 32
Question.2. What is the maximum number of columns in which the CRPF troops can march?
(a) 4
(b) 8
(c) 12
(d) 16
Question.3. What is the maximum number of columns in which total army troops and CRPF troops together can march past?
(a) 2
(b) 4
(c) 6
(d) 8
Question.4. What should be subtracted from the numbers of CRPF soldiers and the number of bikers
so that their maximum number of columns is equal to the maximum number of columns of army troops?
(a) 4 Soldiers and 4 Bikers
(b) 4 Soldiers and 2 Bikers
(c) 2 Soldiers and 4 Bikers
(d) 2 Soldiers and 2 Bikers
Question.5. What should be added with the number of CRPF soldiers and the number of bikers so that their maximum number of columns is equal to the maximum number of columns of army
troops?
(a) 4 Soldiers and 4 Bikers
(b) 12 Soldiers and 12 Bikers
(c) 6 Soldiers and 6 Bikers
(d) 12 Soldiers and 6 Bikers
Ans.1. (b)
16
Ans.2. (c)
12
HCF of 624, 468 and 228
Ans.3. (b)
4
HCF of 228 and 32
Ans.4. (a)
4 Soldiers and 4 Bikers
Maximum no. of columns of army troops = 16 (from ans.1.). But 228 and 468 are not divisible by 16. If we subract 4 from 228 and 468, both 224 and 464 are divisible by 16.
Ans.5. (b)
12 Soldiers and 12 Bikers
Case Study Question 13
Read the following and answer any four questions from 1 to 5 given below:
Traffic Lights (or traffic signals) are lights used to control movement of traffics. They are installed on roads at intersections and crossings. The different colours of light tell drivers what to do. The traffic lights at different road crossings change after every 48 seconds, 72 seconds and 108 seconds respectively.
Question.1. 108 can be expressed as a product of its primes as
(a) 2^{3}\times 3^{2}
(b) 2^{3}\times 3^{3}
(c) 2^{2}\times 3^{2}
(d) 2^{2}\times 3^{3}
Question.2. The HCF of 48, 72, 108 is
(a) 18
(b) 16
(c) 12
(d) 10
Question.3. The LCM of 48, 72, 108 is
(a) 520
(b) 432
(c) 396
(d) 420
Question.4. If all the traffic lights change simultaneously at 8:20:00 hrs, they will again change simultaneously at
(a) 8:27:12 hrs
(b) 8:32:24 hrs
(c) 8:40:08 hrs
(d) 8:24:24 hrs
Question.5. The HCF\times LCM for the numbers 48, 72, 108 is
(a) 2472
(b) 3680
(c) 4090
(d) 5184
Ans.1. (d)
2^{2}\times 3^{3}
Ans.2. (c)
12
Ans.3. (b)
432
Ans.4. (a)
8:27:12 hrs
Ans.5. (d)
5184
Case Study Question 14
Read the following and answer any four questions from 1 to 5 given below:
The Army Day is celebrated on 15th January every year in India. The day is celebrated in the form of parades and other military shows in the national capital New Delhi as well as in all headquarters of army.
Parade I: An Army contingent of 616 members is to march behind an army band of 32 members in parade. The two groups are to march in the same number of columns.
Parade II: An Army contingent of 1000 members is to march behind an army band of 56 members in parade. The two groups are to march in the same number of columns.
Refer to Parade I
Question.1. The expression of 616 as a product of its prime numbers is
(a) 2^{2}\times 14^{1} \times 11^{1}
(b) 2^{3}\times 7^{1} \times 11^{1}
(c) 2^{4}\times 7^{1} \times 11^{1}
(d) None of these.
Question.2. The LCM of 32 and 616 is
(a) 1248
(b) 1836
(c) 2464
(d) 3016
Question.3. What is the maximum number of columns in which they can march?
(a) 6
(b) 8
(c) 10
(d) 12
Refer to Parade II
Question.4. The HCF of numbers 1000 and 56 is
(a) 2
(b) 4
(c) 6
(d) 8
Question.5. Which of the following is the correct expression of the number 1000 as a product of its prime numbers?
(a) 2^{3}\times 5^{3}
(b) 10^{3}
(c) 8\times 125
(d) 8
Ans.1. (b)
2^{3}\times 7^{1} \times 11^{1}
Ans.2. (c)
2464
Ans.3. (b)
8
Ans.4. (d)
8
Ans.5. (a)
2^{3}\times 5^{3}
Case Study Question 15
Read the following and answer any four questions from 1 to 5 given below:
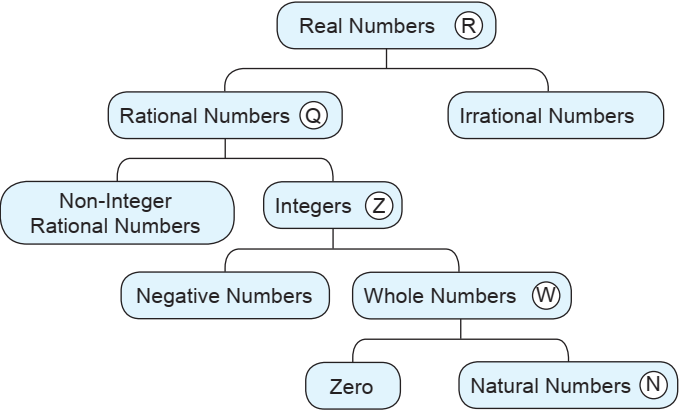
Richard Paul and Linda Elder state that “Thinking is not driven by answers but by questions”. Keeping this idea in mind, mathematics teacher of class X of Blue Marble School decided to develop interest and motivate students to become actively involved in the concept he asked some questions. The teacher drew a flow chart for real numbers family on the board as shown below. The chart for the set of real numerals includes all the types of numbers. Observe the chart carefully.
Question.1. The sum of a rational and irrational number is
(a) Rational
(b) Irrational
(c) both of the above
(d) none of the above
Question.2. The decimal expansion of the number \frac{144}{2^{2}\times 5^{3}\times 7}
(a) Terminating
(b) non-terminating
(c) non-terminating non-repeating
(d) non-terminating repeating
Question.3. A rational number in its decimal expansion is 327.7081. What would be the prime factors of q when the number is expressed in the p/q form?
(a) 2 and 3
(b) 3 and 5
(c) 2, 3 and 5
(d) 2 and 5
Question.4. Which of the following is not irrational?
(a) (3+\sqrt{7})
(b) (3-\sqrt{7})
(c) (3+\sqrt{7})(3-\sqrt{7})
(d) (3\sqrt{7})
Question.5. The decimal expansion of the rational number \frac{14587}{1250} will terminate after:
(a) one decimal place
(b) two decimal places
(c) three decimal places
(d) four decimal places
Ans.1. (b)
Irrational
Ans.2. (d)
Non-terminating repeating
Ans.3. (d)
2 and 5
Ans.4. (c)
(3+\sqrt{7})(3-\sqrt{7})
Ans.5. (d)
four decimal places
Case Study Question 16
Read the following and answer any four questions from 1 to 5 given below:
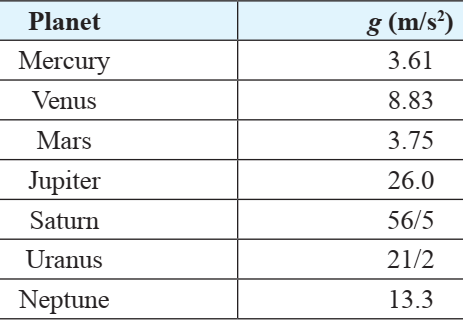
An object when thrown upwards reaches a certain height and then falls downwards. Whenever an object falls towards the earth, acceleration is involved. This acceleration is due to the earth’s gravitational force. Therefore, this acceleration is called the acceleration due to the gravitational force of the earth (or acceleration due to gravity). It is denoted by g. The unit of g is the same as that of acceleration, that is, m/s^{2} . Its value is 9.8 m/s^{2} on Earth. When discussing the acceleration of gravity, it was mentioned that the value of g is dependent upon location. There are slight variations in the value of g on earth’s surface. The following acceleration of gravity values can be calculated for the various planets.
Question.1. Which of the following is the decimal expansion of a rational number?
(a) 26.0
(b) 8.83
(c) 3.75
(d) All of these
Question.2. The p/q form of the number 3.75 will be
(a) 11/4
(b) 17/2
(c) 15/4
(d) None of these
Question.3. An irrational number lying between 8.83 and 11.2 is
(a) 8.8010203040…
(b) 8.9010203040…
(c) 11.10203040…
(d) None of these
Question.4. The decimal expansion of the rational number 56/5 will has
(a) One decimal place
(b) Two decimal places
(c) Three decimal places
(d) Four decimal places
Question.5. The 2^{n}\times 5^{m} form of denominator 21/2 and its decimal expansion respectively are
(a) 2^{0}\times 5^{1}
(b) 2^{1}\times 5^{1}
(c) 2^{0}\times 5^{0}
(d) None of these
Ans.1. (d)
All of these
Ans.2. (c)
15/4
Ans.3. (c)
11.10203040…
Ans.4. (a)
One decimal place
Ans.5. (b)
2^{1}\times 5^{1}
Type 2: Theory type
Case Study Question 17
Read the following and answer the questions given below:
A charitable trust donates 28 different books of Maths, 16 different books of science and 12 different books of Social Science to the poor students. Each student is given maximum number of books of only one subject of his interest and each student got equal number of books.
Question.1. Find the number of books each student got.
Question.2. Find the total number of students who got books.
Ans.1. HCF of 28,16 and 12 is 4
Therefore maximum number of books each student get is 4
Ans.2. Number of maths books 28/4 = 7
Number of science books 16/4 = 4
Number of social science = 12/4 = 3
Total books = 7 + 4 + 3 = 14
Case Study Question 18
Read the following and answer the questions given below:
When the marbles in a bag are divided evenly between two friends, there is one marble left over When the same marbles are divided evenly among three friends, there is one marble left over. When the marbles are divided evenly among five friends, there is one marble left over.
Question.1. What is the least possible number of marbles in the bag?
Question.2. What is another possible number of marbles in the bag?
Ans.1. LCM of 2, 3 and 5 = 30
Thus 31 marbles are there in the bag.
Ans.2. If we add 1 in multiple of 30 we will get another possible number of marble. These are 61, 91, 121, …
Case Study Question 19
Read the following and answer the questions given below:
Kerosene, paraffin, or lamp oil is a combustible hydrocarbon liquid which is derivative from petroleum. Kerosen’s uses vary from fuel for oil lamps to cleaning agents, jet fuel, heating oil or fuel for cooking. Two oil tankers contain 825 litres and 675 litres of kerosene oil respectively.
Question.1. Find the maximum capacity of a container which can measure the Kerosene oil of both the tankers when used an exact number of times.
Question.2. How many times we have to use container for both the tanker to fill?
Ans.1. HCF of 825 and 625
825 = 3\times 5\times 5\times 11
675 = 3\times 3\times 3\times 5\times 5
HCF = 3\times 5\times 5 = 75
Maximum capacity reqired is 75 litres
Ans.2. The first tanker will require 875/75 = 11 times to fill
The second tanker will require 675/75 = 9 times to fill.
Case Study Question 20
Read the following and answer any four questions from 1 to 5 given below:
Amar, Akbar and Anthony are playing a game. Amar climbs 5 stairs and gets down 2 stairs in one turn. Akbar goes up by 7 stairs and comes down by 2 stairs every time. Anthony goes 10 stairs up and 3 stairs down each time. During this they have to reach to the nearest point of 100th stairs and they will stop once they find it impossible to go forward. They can not cross 100th stair any way.
Question.1. Who reaches the nearest point?
Question.2. Who takes least number of steps to reach nearest hundred?
Ans.1. Amar reaches 96 stairs
Akbar reaches 95 stairs
Anthony reaches 91 stairs
Thus Amar will reach nearest point
Ans.2. Amar will take 100/3 = 33.3
Akbar will take 100/5 = 20
Anthony will take 100/7 = 14.22
Anthony will take least step.
Case Study Question 21
Read the following and answer the questions given below:
A woman wants to organise her birthday party. She was happy on her birthday but there was a problem that she does not want to serve fast food to her guests because she is very health conscious. She as 15 apples and 40 bananas at home and decided to serve them. She want to distribute fruits among guests. She does not want to discriminate among guests so she decided to distribute equally among all.
Question.1. How many guests she can invite?
Question.2. How many apples and banana will each guest get?
Ans.1. HCF of (15,40) = 5
Fruits will be distributed equally among 5 guests
Ans.2. Out of 15 apples each guest will get 15 /5 = 3 apples
Out of 40 banana each guest will get 40/5 =8 bananas.
Case Study Question 22
Read the following and answer the questions given below:
A hall has a certain number of chairs. Guests want to sit in different groups like in pairs, triplets, quadruplets, fives and sixes etc. When organiser arranges chairs in
such pattern like 2’s, 3’s, 4’s, 5’s and 6’s then 1, 2, 3, 4 and 5 chairs are left respectively. But when he arranges in 11’s no chair will be left.
Question.1. In the hall how many chairs are available?
(a) 407
(b) 143
(c) 539
(d) 209
Question.2. If one chair is added to the total number of chairs, how many chairs will be left when arranged in 11’s
Ans.1. 539 chairs.
Ans.2. if 1 chair is added as 539 is already divisible by 11 ,1 chair will be left.
Case Study Question 23
Read the following and answer the questions given below:
Flipkart is an Indian e-commerce company , headquartered in Bangalore, Karnataka and incorporated in Singapore as a private limited company . The company initially focussed on online book sales before expanding into other product categories such as consumer electronics fashion, home essentials groceries and lifestyle products. Flipkart sells 10 types of items which are packed into various sizes of cartons which are packed into various size of cartons which are given below: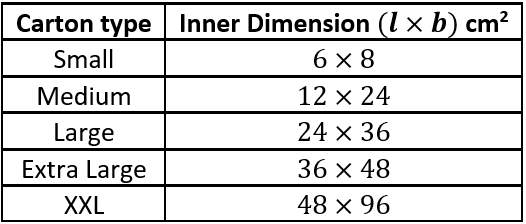
Question.1. What should be the maximum size of the sheet that fits into all type of cartons?
Question.2. What should have been size of semi large (which is larger than medium carton but smaller than large carton) so that the maximum sized sheet remains same?
Ans.1. HCF of all length
HCF(6, 12, 24, 36, 48) = 6
Ans.2. HCF of all width
HCF(8, 24, 36, 48, 96) = 4
Thus maximum size of sheet is 6 by 4
Case Study Question 24
Read the following and answer the questions given below:
Kartik is a salesman of mobile phones. His yearly target is to sell a fixed number of mobile phones in a year. He planned to meet \frac{6}{11} of his yearly target by selling the phones during a festive month. He could only meet \frac{6}{11} of his target for the festive month. He now has to meet the remaining target for the month and sell 425 more mobile phones to meet his yearly target.
Question.1. Approximately what percentage of the yearly target was met during the festive month?
Question.2. How many units of the mobile phones did Kartik have to sell to meet his yearly target?
Ans.1.
30% or 30
Ans.2.
2057
Case Study Question 25
Read the following and answer the questions given below:
Aadya has 143 stamps; she gives away 11 stamps and divides the remaining equally into groups. Sumit has 220 stamps; he gives away 11 stamps and divides the remaining equally into groups. They end up with the same number of groups.
Question.1. What is the number of groups?
Question.2. What is the number of stamps in Adya’s and Sumit’s groups?
Ans.1.
11
Ans.2.
Adya’s groups have 12 stamps each and Sumit’s groups have 19 stamps each
- 19, 12
- 12, 19
12 stamps and 19 stamps
Case Study Question 26
Read the following and answer the questions given below:
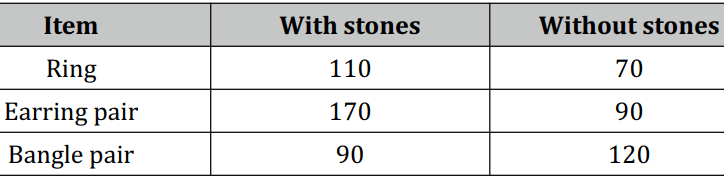
Richa is an artificial jewellery seller. She buys them from a dealer at a price based on the presence or absence of stones as shown in the table below.
Question.1. For every ring with stones, two rings without stones are purchased by Richa’s customers. Richa buys rings accordingly from the dealer for Rs .10 000. How many rings does she buy?
Question.2. In her next visit to the dealer, Richa finds that dealer has increased the price of rings with stones by Rs. 10. Richa still wants to spend Rs. 10 000 on rings. What is the reduction in the number of rings she buys?
(a) 10
(b) 20
(c) 40
(d) 50
Question.3. The dealer increases the price of one type of earrings. Richa buys earrings (with stones and without stones) in the ratio of 5:9 before the price hike. After the price hike, she buys earrings in the ratio of 8:13 with the same amount of money. Does she buy more earrings with stones than earrings without stones after the price hike? Give reasons.
Question.4. Richa purchases 37 pairs of bangles with stones and 33 pairs of bangles without stones. She divides them into two sets. Set 1 contains 40 pairs of bangles, and set 2 contains 30 pairs of bangles. What is the difference between the number of bangle pairs with stones in set 1 and the number of bangle pairs without stones in set 2?
(a) 4
(b) 7
(c) 10
(d) 30
Question.5. Despite the price hike by the dealer, Richa increases the number of jewellery with stones she purchases for her customers. What could be the reason for her decision?
Ans.1.
120
Ans.2. (b)
20
Ans.3.
‘Yes’ and that the ratio 8:13 is more than 5:19
Yes, 8:13 > 5:19, thus she had bought more earrings with stones after the price hike
Ans.4. (b)
7
Ans.5.
Writes an explanation which predicts the trend. For example:
The demand for jewelry with stones among customers increases.
People prefer to buy jewelry with stones.