What is Case Study Question / Paragraph Based Question?
A case study is a scenario in a particular academic / professional context which students are expected to analyse and respond to, guided by specific questions posed concerning the situation. In many cases, the scenario or case study involves a number of issues or problems that must be dealt with in a academic / professional workplace.
Why Case Study Questions are included in academics?
Case study assignments usually require students to identify problems and issues in a scenario, to demonstrate their developing knowledge of theories and academic / professional policies and to make decisions and recommendations based on these to either prevent or solve some of the issues in that scenario.
How to solve Case Study Questions?
There are several steps to writing an answer to a case study assignment:
STEP 1: Read the case study and questions carefully.
- Read the case and associated questions carefully.
- Highlight the main points of the case and any issues that you can identify.
- Read the questions closely and analyse what they are requiring you to do.
- Read the case again, linking the information that is relevant to each question you have been asked.
STEP 2: Identify the issues in the case study.
Case studies describe a situation which may arise in a particular profession or social context. They often involve a number of people in a complex situation. They will often describe a situation which is problematic, possibly in how it is dealt with, or in its complexity. An important part of your answer is to analyse the situation and to identify the issues/actions described in the case which may be problematic. The following questions may help you to do this:
- What actions were taken in the case?
- Were these actions the most appropriate and why?
- Were there any consequences of the actions taken?
- Was anything omitted or not considered?
- Were actions/procedures in line with existing codes of practice, policy or theories?
STEP 3: Link theory to practice.
Use your knowledge of existing codes of practice, theories and/or other academic / professional documents and behaviours to decide what was done appropriately and what was not.
STEP 4: Plan your answer.
It can be useful to use the questions you have been set as headings and to answer each part in turn, reducing the chance of omitting set questions. You can always take out the headings before you submit if you wish. Lecturers usually set questions in a logical order, so answer in the order they are written in your question.
STEP 5: Start writing your case study answer (for theory only)
Like any assignment, you will need an introduction, body sections in which you answer the questions put to you regarding the case study, and a conclusion.
STEP 6: Edit and proofread.
Read through your paper yourself to detect and correct other errors and omissions.
Check you have answered all questions and backed up your answer with relevant passage.
Types of Case Study Questions / Paragraph Based Questions
Case Study Questions / Paragraph Based Questions can be broadly classified into two types:
- MCQs type: In this type, student has to tick the correct option from various options.
- Theory type: In this type, student has to write proper solution / answer in cotext to the case study.
Case Study/ Passage Based Questions Chapter 3 Pair of Linear Equations in Two Variables Mathematics
Type 1: MCQ type
Case Study Question 01
Read the following and answer any four questions from 1 to 5 given below:
From a shop, Sudhir bought 2 books of Mathematics and 3 books of Physics of class X for ₹ 850 and Suman bought 3 books of Mathematics and 2 books of Physics of class X for ₹ 900. Consider the price of one Mathematics book and that of one Physics book be ₹ x and ₹ y respectively.
Based on the above information, answer the following questions.
Question.1. Represent the situation faced by Sudhir, algebraically.
(a) 2x+3y=850
(b) 3x+2y=850
(c) 2x-3y=850
(d) 3x-2y=850
Question.2. Represent the situation faced by Suman, algebraically.
(a) 2x+3y=90
(b) 3x+2y=900
(c) 2x-3y=900
(d) 3x-2y=900
Question.3. The price of one Physics book is
(a) ₹ 80
(b) ₹ 100
(c) ₹ 150
(d) ₹ 200
Question.4. The price of one Mathematics book is
(a) ₹ 80
(b) ₹ 100
(c) ₹ 150
(d) ₹ 200
Question.5. The system of linear equations represented by above situation, has
(a) unique solution
(b) no solution
(c) infinitely many solutions
(d) none of these
Ans.1. (a)
Situation faced by Sudhir can be represented algebraically as
2x + 3y = 850
Ans.2. (b)
Situation faced by Suman can be represented algebraically as
3x + 2y = 900
Ans.3. (c)
We have
2x + 3y = 850 …(i)
and 3x + 2y = 900 …(ii)
Multiplying (i) by 3 and (ii) by 2 and subtracting, we get
5y=750
⇒ y= 150
Thus, price of one Physics book is ₹ 150.
Ans.4. (d)
From equation (i) we have, 2x+3 \times 150=850
⇒ 2x=850-450=400
⇒ x=200
Hence, cost of one Mathematics book = ₹ 200
Ans.5. (a)
From above, we have
a_{1}=2, b_{1}=3, c_{1}=-850 and a_{2}=3, b_{2}=2, c_{2}=-900
∴ \frac{a_{1}}{a_{2}}=\frac{2}{3}, \frac{b_{1}}{b_{2}}=\frac{3}{3}, \frac{c_{1}}{c_{2}}=\frac{-850}{-900}=\frac{17}{18}
⇒ \frac{a_{1}}{a_{2}}≠\frac{b_{1}}{b_{2}}≠\frac{c_{1}}{c_{2}}
Thus system of linear equations has unique solution.
Case Study Question 02
Read the following and answer any four questions from 1 to 5 given below:
A boat in the river Ganga near Rishikesh covers 24 km upstream and 36 km downstream in 6 hours while it covers 36 km upstream and 24 km downstream in 6\frac{1}{2} hours. Consider speed of the boat in still water be x km/hr and speed of the stream be y km/hr and answer the following questions.
Question.1. Represent the 1^{st} situation algebraically.
(a) \frac{24}{x-y}+\frac{36}{x+y}=6
(b) \frac{24}{x+y}+\frac{36}{x-y}=6
(c) 24x+36y=6
(d) 24x-36y=6
Question.2. Represent the 2^{nd} situation algebraically.
(a) \frac{36}{x+y}+\frac{24}{x-y}=\frac{13}{2}
(b) \frac{36}{x-y}+\frac{24}{x+y}=\frac{13}{2}
(c) 36x-24y= \frac{13}{2}
(d) 36x+24y= \frac{13}{2}
Question.3. If u= \frac{1}{x-y} and v= \frac{1}{x+y} , then u=
(a) \frac{1}{4}
(b) \frac{1}{12}
(c) \frac{1}{8}
(d) \frac{1}{6}
Question.4. Speed of boat in still water is
(a) 4 km/hr
(b) 6 km/hr
(c) 8 km/hr
(d) 10 km/hr
Question.5. Speed of stream is
(a) 3 km/hr
(b) 4 km/hr
(c) 2 km/hr
(d) 5 km/hr
Speed of boat in upstream = (x-y) km/hr and
speed of boat in downstream = (x+y) km/hr.
Ans.1. (a)
1^{st} situation can be represented algebraically as
\frac{24}{x-y}+\frac{36}{x+y}=6
Ans.2. (b)
2^{nd} situation can be represented algebraically as
\frac{36}{x-y}+\frac{24}{x+y}=\frac{13}{2}
Ans.3. (c)
Putting \frac{1}{x-y}=u and \frac{1}{x+y}=v , we get
24u+36v=6 and
36u+24v= \frac{13}{2}
Solving the above equations, we get u=\frac{1}{8}, v= \frac{1}{12}
Ans.4. (d)
∵ u= \frac{1}{8}= \frac{1}{x-y}
⇒ x-y=8 …(i)
and v= \frac{1}{12}= \frac{1}{x+y}
⇒ x+y=12 …(ii)
Adding equations (i) from (ii), we get
2x=20
⇒ x=10
Speed of boat in still water = 10 km/hr
Ans.5. (c)
From equation (i), 10-y=8
⇒ y=2
∴ Speed of stream = 2 km/hr
Case Study Question 03
Read the following and answer any four questions from 1 to 5 given below:
Piyush sells a saree at 8% profit and a sweater at 10% discount, thereby, getting a sum of ₹ 1008. If he had sold the saree at 10% profit and the sweater at 8% discount, he would have got ₹ 1028. Denote the cost price of the saree and the list price (price before discount) of the sweater by ₹ x and ₹ y respectively and answer the following questions.
Question.1. The 1^{st} situation can be represented algebraically as
(a) 2.08x+1.9y=2008
(b) 1.08x+0.9y=1008
(c) 10x+8y=1008
(d) 8x+10y=1008
Question.2. The 2^{nd} situation can be represented algebraically as
(a) 10x+8y=1028
(b) 2.1x+1.92y=1028
(c) 1.1x+0.92y=1028
(d) 8x+10y=1028
Question.3. Linear equation represented by 1^{st} situation intersect the x-axis at
(a) (2800, 0)
(b) (2500, 0)
(c) \left(\frac{2500}{3}, 0\right)
(d) \left(\frac{2800}{3}, 0\right)
Question.4. Linear equation represented by 2^{nd} situation intersect the y-axis at
(a) \left(0, \frac{25700}{23}\right)
(b) (0, 25700)
(c) \left(0, \frac{25800}{23}\right)
(d) (0, 26800)
Question.5. Both linear equations represented by situation 1^{st} and 2^{nd} intersect each other at
(a) (400, 600)
(b) (600, 400)
(c) (200, 200)
(d) (800, 600)
Ans.1. (b)
Piyush sells a saree at 8% profit + sells a sweater at 10% discount = ₹ 1008
⇒ (100+8)% of x + (100-10)% of y = 1008
⇒ 108% of x + 90% of y = 1008 …(i)
Ans.2. (c)
Piyush sold the saree at 10% profit + sold the sweater at 8% discount = ₹ 1028
⇒ (100+10) % of x + (100-8) % of y = 1028
⇒ 110% of x + 92% of x = 1028
⇒ 1.1x+0.92y= 1028 …(ii)
Ans.3. (d)
At x-axis, y=0
1.08x=1008
⇒ x= \frac{1008}{1.08}=\frac{2800}{3}
Ans.4. (a)
At y-axis, x=0
⇒ 0.92y=1028
⇒ y= \frac{1028}{0.92}=\frac{25700}{23}
Ans.5. (b)
Solving equations (i) and (ii), we get
x = 600 and y = 400
Hence both linear equations intersect at (600, 400).
Case Study Question 04
Read the following and answer any four questions from 1 to 5 given below:
Puneet went for shopping in the evening by metro with his father who is an expert in mathematics. He told Puneet that path of metro A is given by the equation 2x+4y=8 and path of metro B is given by the equation 3x+6y=18.
His father put some questions to Puneet. Help Puneet to solve the questions.
Question.1. Equation 2x+4y=8 intersects the x-axis and y-axis respectively at
(a) (4, 0), (0, 2)
(b) (0, 4), (2, 0)
(c) (4, 0), (2, 0)
(d) (0, 4), (0, 2)
Question.2. Equation 3x+6y=18 intersects the x-axis and y-axis respectively at
(a) (6, 0), (0, 8)
(b) (0, 6), (0, 8)
(c) (6, 0), (0, 3)
(d) (0, 6), (0, 3)
Question.3. Coordinates of point of intersection of two given equations are
(a) (1, 2)
(b) (2, 4)
(c) (3, 7)
(d) does not exist
Question.4. Represent the equations, 2x+4y=8 and 3x+6y=18 graphically.
(a) 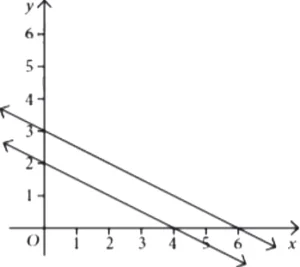
Question.5. System of linear equations represented by two given lines is
(a) inconsistent
(b) having infinitely many solutions
(c) consistent
(d) overlapping each other
Ans.1. (a)
At x-axis, y=0
∴ 2x+4y=8
⇒ x=4
At y-axis, x=0
∴ 2x+4y=8
⇒ y=2
∴ Required coordinates are (4, 0), (0, 2).
Ans.2. (c)
At x-axis, y=0
∴ 3x+6y=18
⇒ 3x=18
⇒ x=6
At y-axis, x=0
∴ 3x+6y=18
⇒ 6y=18
⇒ y=3
∴ Required coordinates are (6, 0), (0, 3).
Ans.3. (d)
Since, lines are parallel.
So, point of intersection of these lines does not exist.
Ans.4. (a)
Ans.5. (a)
Since the lines are parallel.
∴ These equations have no solution i.e., the given system of linear equations is inconsistent.
Case Study Question 05
Read the following and answer any four questions from 1 to 5 given below:
Raman usually go to a dry fruit shop with his mother. He observes the following two situations.
On 1^{st} day: The cost of 2 kg of almonds and 1 kg of cashew was ₹ 1600.
On 2^{nd} day: The cost of 4 kg of almonds and 2 kg of cashew was ₹ 3000.
Denoting the cost of 1 kg almonds by ₹ x and cost of 1 kg cashew by ₹ y, answer the following questions.
Question.1. Represent algebraically the situation of day-I.
(a) x+2y=1000
(b) 2x+y=1600
(c) x-2y=1000
(d) 2x-y=1000
Question.2. Represent algebraically the situation of day-II.
(a) 2x+y=1500
(b) 2x-y=1500
(c) x+2y=1500
(d) 2x+y=750
Question.3. The linear equation represented by day-I, intersect the x-axis at
(a) (0, 800)
(b) (0, -800)
(c) (800, 0)
(d) (-800, 0)
Question.4. The linear equation represented by day-II, intersect the y-axis at
(a) (1500, 0)
(b) (0, -1500)
(c) (-1500, 0)
(d) (0, 1500)
Question.5. Linear equations represented by day-I and day -II situations, are
(a) non parallel
(b) parallel
(c) intersect at one point
(d) overlapping each other.
Ans.1. (b)
Algebraic representation of situation of day-I is
2x+y=1600
Ans.2. (a)
Algebraic representation of situation of day-II is
4x+2y=3000
⇒ 2x+y=1500
Ans.3. (c)
At x-axis, y=0
∴ At y=0,
2x+y= 1600 becomes 2x = 1600
⇒ x=800
∴ Linear equation represented by day-I intersect the x-axis at (800, 0).
Ans.4. (d)
At y-axis, x=0
∴ 2x+y=1500
⇒ y=1500
Linear equation represented by day-II intersect the y-axis at (0, 1500).
Ans.5. (b)
We have, 2x+y=1600
and 2x+y=1500
Since \frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}≠\frac{c_{1}}{c_{2}} i.e.,
\frac{1}{1}=\frac{1}{1}≠\frac{16}{15}
∴ System of equations have no solution.
∴ Lines are parallel.
Case Study Question 06
Read the following and answer any four questions from 1 to 5 given below:
A part of monthly hostel charges in a college is fixed and the remaining depends on the number of days one has taken food in the mess. When a student Anu takes food for 25 days, she has to pay ₹ 4500 as hostel charges, whereas another student Bindu who takes food for 30 days, has to pay ₹ 5200 as hostel charges.
Considering the fixed charges per month be ₹ x and the cost of food per day be ₹ y, then answer the following questions.
Question.1. Represent algebraically the situation faced by both Anu and Bindu.
(a) x+25y=4500, x+30y=5200
(b) 25x+y=4500, 30x+y=5200
(c) x-25y=4500, x-30y=5200
(d) 25x-y=4500, 30x-y=5200
Question.2. The system of linear equations, represented by above situations has
(a) No solution
(b) Unique solution
(c) Infinitely many solutions
(d) None of these
Question.3. The cost of food per day is
(a) ₹ 120
(b) ₹ 130
(c) ₹ 140
(d) ₹ 1300
Question.4. The fixed charges per month for the hostel is
(a) ₹ 1500
(b) ₹ 1200
(c) ₹ 1000
(d) ₹ 1300
Question.5. If Bindu takes food for 20 days, then what amount she has to pay?
(a) ₹ 4000
(b) ₹ 3500
(c) ₹ 3600
(d) ₹ 3800
Ans.1. (a)
For student Anu: Fixed charge + cost of food for 25 days = ₹ 4500 i.e., x+25y=4500
For student Bindu: Fixed charges + cost of food for 30 days = ₹ 5200 i.e., x+30y=5200
Ans.2. (b)
From above, we have a_{1}=1, b_{1}=25, c_{1}=-4500 and a_{2}=1, b_{2}=30, c_{2}=-5200
∴ \frac{a_{1}}{a_{2}}=1, \frac{b_{1}}{b_{2}}=\frac{25}{30}=\frac{5}{6}, \frac{c_{1}}{c_{2}}=\frac{-4500}{-5200}=\frac{45}{52}
⇒ \frac{a_{1}}{a_{2}}≠\frac{b_{1}}{b_{2}}≠\frac{c_{1}}{c_{2}}
Thus, system of linear equations has unique solution.
Ans.3. (c)
We have, x+25y=4500 …(i)
and x+30y=5200 …(ii)
Subtracting (i) from (ii), we get
5y=700
⇒y= 140
∴ Cost of food per day is ₹ 140
Ans.4. (c)
We have, x+25y=4500
⇒x=4500-25 \times 140
⇒x=4500-3500=1000
∴ Fixed charges per month for the hostel is ₹ 1000
Ans.5. (d)
We have, x=1000, y=140 and Bindu takes food for 20 days.
∴ Amount that Bindu has to pay = (1000+ 20 \times 140) = ₹ 3800
Case Study Question 07
Read the following and answer any four questions from 1 to 5 given below:
From Bengaluru bus stand, if Riddhima buys 2 tickets to Malleswaram and 3 tickets to Yeswanthpur, then total cost is ₹ 46; but if she buys 3 tickets to Malleswaram and 5 tickets to Yeswanthpur, then total cost is ₹ 74.
Consider the fares from Bengaluru to Malleswaram and that to Yeswanthpur as ₹ x and ₹ y respectively and answer the following questions.
Question.1. 1^{st} situation can be represented algebraically as
(a) 3x-5y=74
(b) 2x+5y=74
(c) 2x-3y=46
(d) 2x+3y=46
Question.2. 2^{nd} situation can be represented algebraically as
(a) 5x+3y=74
(b) 5x-3y=74
(c) 3x+5y=74
(d) 3x-5y=74
Question.3. Fare from Bengaluru to Malleswaram is
(a) ₹ 6
(b) ₹ 8
(c) ₹ 10
(d) ₹ 2
Question.4. Fare from Bengaluru to Yeswanthpur is
(a) ₹ 10
(b) ₹ 12
(c) ₹ 14
(d) ₹ 16
Question.5. The system of linear equations represented by both situations has
(a) infinitely many solutions
(b) no solution
(c) unique solution
(d) none of these
Ans.1. (d)
1^{st} situation can be represented algebraically as
2x+3y=46
Ans.2. (c)
2^{nd} situation can be represented algebraically as 3x+5y=74
Ans.3. (b)
We have, 2x+3y=46 … (i)
3x+5y=74 … (ii)
Multiplying (i) by 5 and (ii) by 3 and then subtracting, we get
10x-9x=230-222
⇒ x=8
∴ Fare from Bengaluru to Malleswaram is ₹ 8.
Ans.4. (a)
Putting the value of x in equation (i), we get
3y=46-2 \times 8 = 30
⇒ y=10
∴ Fare from Bengaluru to Yeswanthpur is ₹ 10.
Ans.5. (c)
We have, a_{1}=2, b_{1}=3, c_{1}=-46 and a_{2}=3, b_{2}=5, c_{2}=-74
∴ \frac{a_{1}}{a_{2}}=\frac{2}{3}, \frac{b_{1}}{b_{2}}=\frac{3}{5}, \frac{c_{1}}{c_{2}}=\frac{-46}{-74}=\frac{23}{37}
⇒ \frac{a_{1}}{a_{2}}≠\frac{b_{1}}{b_{2}}≠\frac{c_{1}}{c_{2}}
Thus system of linear equations has unique solution.
Case Study Question 08
Read the following and answer any four questions from 1 to 5 given below:
Points A and B representing Chandigarh and Kurukshetra respectively are almost 90 km apart from each other on the highway. A car starts from Chandigarh and another from Kurukshetra at the same time. If these cars go in the same direction, they meet in 9 hours and if these cars go in opposite direction they meet in 9/7 hours. Let X and y be two cars starting from points A and B respectively and their speed be x km/hr and y km/hr respectively. Then, answer the following questions.
Question.1. When both cars move in the same direction, then the situation can be represented algebraically as
(a) x-y=10
(b) x+y=10
(c) x+y=9
(d) x-y=9
Question.2. When both cars move in opposite direction, then the situation can be represented algebraically as
(a) x-y=70
(b) x+y=90
(c) x+y=70
(d) x+y=10
Question.3. Speed of car X is
(a) 30 km/hr
(b) 40 km/hr
(c) 50 km/hr
(d) 60 km/hr
Question.4. Speed of car Y is
(a) 50 km//hr
(b) 40 km/hr
(c) 30 km/hr
(d) 60 km/hr
Question.5. If speed of car X and car Y, each is increased by 10 km/hr, and cars are moving in opposite direction, then after how much time they will meet?
(a) 5 hrs
(b) 4 hrs
(c) 2 hrs
(d) 1 hr
Ans.1. (a)
Suppose two cars meet at point Q.
Then, Distance travelled by car X = AQ,
Distance travelled by car Y = BQ.
It is given that two cars meet in 9 hours.
∴ Distance travelled by car X in 9 hours = 9x km
⇒ AQ = 9x
Distance travelled by car Y in 9 hours = 9y km
⇒ BQ = 9y
Clearly, AQ – BQ = AB
⇒ 9x-9y=90
⇒ x-y=10
Ans.2. (c)
Suppose two cars meet at point P. Then Distance travelled by car X = AP and
Distance travelled by car Y = BP.
In this case, two cars meet in 9/7 hours.
∴ Distance travelled by car X in 9/7 hours = \frac{9}{7}x km
⇒ AP = \frac{9}{7}x
Distance travelled by car Y in 9/7 hours = \frac{9}{7}y km
⇒ BP = \frac{9}{7}y
Clearly, AP + BP = AB
⇒ \frac{9}{7}x + \frac{9}{7}y = 90
⇒ \frac{9}{7}(x+y)=90
⇒ x+y=70
Ans.3. (b)
We have x-y=10 …(i)
⇒ x+y=70 …(ii)
Adding equations (i) and (ii), we get
2x=80
⇒ x=40
Hence, speed of car X is 40 km/hr.
Ans.4. (c)
We have x-y=10
⇒ 40-y=10
⇒ y=30
Hence, speed of car Y is 30 km/hr
Ans.5. (d)
Case Study Question 09
Read the following and answer any four questions from 1 to 4 given below:
Mr Manoj Jindal arranged a lunch party for some of his friends. The expense of the lunch are partly constant and partly proportional to the number of guests. The expenses amount to ₹ 650 for 7 guests and ₹ 970 for 11 guests.
Denote the constant expense by ₹ x and proportional expense per person by ₹ y and answer the following questions.
Question.1. Represent both the situations algebraically.
(a) x+7y=650, x+11y=970
(b) x-7y=650, x-11y=970
(c) x+11y=650, x+7y=970
(d) 11x+7y=650, 11x-7y=970
Question.2. Proportional expense for each person is
(a) ₹ 50
(b) ₹ 80
(c) ₹ 90
(d) ₹ 100
Question.3. The fixed (or constant) expense for the party is
(a) ₹ 50
(b) ₹ 80
(c) ₹ 90
(d) ₹ 100
Question.4. If there would be 15 guests at the lunch party, then what amount Mr Jindal has to pay?
(a) ₹ 1500
(b) ₹ 1300
(c) ₹ 1200
(d) ₹ 1290
Question.5. The system of linear equations representing both the situations will have
(a) unique solution
(b) no solution
(c) infinitely many solutions
(d) none of these
Ans.1. (a)
1st situation can be represented as
x+7y=650 …(i)
and 2nd situation can be represented as
x+11y=970 …(ii)
Ans.2. (b)
Subtracting equations (i) from (ii), we get
4y=320
⇒ y=80
∴ Proportional expense for each person is ₹ 80.
Ans.3. (c)
Putting y = 80 in equation (i), we get x+7 \times 80 = 650
⇒ x= 650-560 = 90
.. Fixed expense for the party is ₹ 90
Ans.4. (d)
If there will be 15 guests, then amount that Mr Jindal has to pay
= ₹(90 + 15 \times 80) = ₹ 1290
Ans.5. (a)
We have, a_{1}=1, b_{1}=7, c_{1}=-650 and a_{2}=1, b_{2}=11, c_{2}=-970
∴ \frac{a_{1}}{a_{2}}=1, \frac{b_{1}}{b_{2}}=\frac{7}{11}, \frac{c_{1}}{c_{2}}=\frac{-650}{-970}=\frac{65}{97}
⇒ \frac{a_{1}}{a_{2}}≠\frac{b_{1}}{b_{2}}≠\frac{c_{1}}{c_{2}}
Thus system of linear equations has unique solution.
Case Study Question 10
Read the following and answer any four questions from 1 to 5 given below:
In a office, 8 men and 12 women together can finish a piece of work in 10 days, while 6 men and 8 women together can finish it in 14 days. Let one day’s work of a man be \frac{1}{x} and one day’s work of a woman be \frac{1}{y} .
Based on the above information, answer the following questions.
Question.1. 1^{st} situation can be represented algebraically as
(a) \frac{80}{x}-\frac{120}{y}=1
(b) \frac{120}{x}-\frac{80}{y}=1
(c) \frac{120}{x}+\frac{80}{y}=1
(d) \frac{80}{x}+\frac{120}{y}=1
Question.2. 2^{nd} situation can be represented algebraically as
(a) \frac{112}{x}-\frac{84}{y}=1
(b) \frac{84}{x}-\frac{112}{y}=1
(c) \frac{84}{x}+\frac{112}{y}=1
(d) \frac{112}{x}+\frac{84}{y}=1
Question.3. One woman alone can finish the work in
(a) 220 days
(b) 140 days
(c) 280 days
(d) 160 days
Question.4. One man alone can finish the work in
(a) 140 days
(b) 220 days
(c) 160 days
(d) 280 days
Question.5. If 14 men and 28 women work together, then in what time, the work will be completed?
(a) 2 days
(b) 3 days
(c) 4 days
(d) 5 days
Ans.1. (d)
Since 8 men and 12 women can finish the work in 10 days.
∴ \left(\frac{8}{x}+\frac{12}{y}\right)=\frac{1}{10}
⇒ \left(\frac{80}{x}+\frac{120}{y}\right)=1
Ans.2. (c)
Since 6 men and 8 women can finish a piece of work in 14 days.
∴ \left(\frac{6}{x}+\frac{8}{y}\right)=\frac{1}{14}
⇒ \left(\frac{84}{x}+\frac{112}{y}\right)=1
Ans.3. (c)
Let \frac{1}{x}=u , \frac{1}{y}=v
Thus, we have
80u + 120v = 1 and
84u + 112y = 1
Solving above two equations, we get
v=\frac{1}{280}
⇒ \frac{1}{y}=\frac{1}{280}
⇒ y=280
Thus one woman alone can finish the work in 280 days.
Ans.4. (a)
We have
⇒ \left(\frac{80}{x}+\frac{120}{y}\right)=1
⇒ \left(\frac{80}{x}+\frac{120}{280}\right)=1
⇒ \frac{80}{x}=1-\frac{3}{7}
⇒ \frac{80}{x}=\frac{4}{7}
⇒ x=140
Thus one man alone can finish the work in 140 days.
Ans.5. (d)
We have, x=140 and y=280
One day’s work of 14 men and 28 women
= \frac{14}{140}+\frac{28}{280}
= \frac{1}{10}+\frac{1}{10}
= \frac{2}{10}
⇒ \frac{1}{5}
Thus, work will be finished in 5 days.
Case Study Question 11
Read the following and answer any four questions from 1 to 4 given below:
A test consists of ‘True’ or ‘False’ questions. One mark is awarded for every correct answer while ¼ mark is deducted for every wrong answer. A student knew answers to some of the questions. Rest of the questions he attempted by guessing.
Question.1. If answers to all questions that he attempted by guessing were wrong, how many questions did he answer correctly?
(a) 96
(b) 86
(c) 76
(d) 106
Question.2. How many questions did he guess?
(a) 12
(b) 18
(c) 24
(d) 26
Question.3. If answers to all the questions he attempted by guessing were wrong and answered 80 correctly, then how many marks did he get?
(a) 50
(b) 70
(c) 80
(d) 20
Question.4. If answers to all the questions he attempted by guessing were wrong, then how many questions did answer correctly to score 95 marks?
(a) 100
(b) 200
(c) 250
(d) 150
Ans.1. (a) 96
Let the no. of questions whose answers are known to the student x and questions attempted by guessing be y .
x+y=120 …(i)
x- \frac{1}{4}=90 …(ii)
Solving (i) and (ii), we get x = 96 and y = 24
∴ No. of questions whose answer are known = 96
Ans.2. (c) 24
Ans.3. (b) 70
Total no. of questions = 96 + 24 = 120
Marks = 80 – \frac{1}{4} of 40 = 70
Ans.4. (a) 100
x- \frac{1}{4} of (120 – x) = 95
⇒ 5x = 380 + 120
⇒ 5x = 500
⇒ x = 100
Case Study Question 12
Read the following and answer any four questions from 1 to 5 given below:
Amit is planning to buy a house and the layout is given below. The design and the measurement has been made such that areas of two bedrooms and kitchen together is 95 sq.m.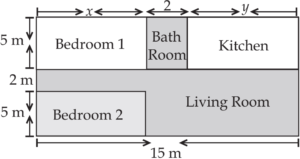
Question.1. Which is the correct equation in two variables from this situation.
(a) x+y=13
(b) x+y=15
(c) x+y=17
(d) x+y=19
Question.2. Find the length of the outer boundary of the layout.
(a) 86 m
(b) 45 m
(c) 34 m
(d) 54 m
Question.3. Find the area of each bedroom and kitchen in the layout.
(a) Bedroom 20 m^{2}; Kitchen 25 m^{2}
(b) Bedroom 50 m^{2}; Kitchen 55 m^{2}
(c) Bedroom 30 m^{2}; Kitchen 35 m^{2}
(d) Bedroom 40 m^{2}; Kitchen 45 m^{2}
Question.4. Find the area of living room in the layout.
(a) 85 m^{2}
(b) 65 m^{2}
(c) 45 m^{2}
(d) 75 m^{2}
Question.5. Find the cost of laying tiles in kitchen at the rate of ₹ 50 per sq.m.
(a) ₹ 1850
(b) ₹ 1750
(c) ₹ 1950
(d) ₹ 1650
Ans.1. (a)
⇒ x+2+y=15
∴ x+y=13
Ans.2. (d) 54 m
Length = 12 + 15 + 12 + 15 = 54 m
Ans.3. (c) Bedroom 30 m^{2}; Kitchen 35 m^{2}
Area of two bedrooms = 5x + 5x = 10x m^{2}
Area of Kitchen = 5y m^{2}
According to Question, 10x + 5y = 95 …(i)
x + y = 13 …[From point (i)]
Solving the above, we get x = 6 and y = 7
∴ Area of each Bedroom = 5x = 30 m^{2}
∴ Area of the Kitchen = 5y = 35 m^{2}
Ans.4. (d) 75 m^{2}
Total Area = 15 \times 12 = 180 m^{2}
Area of Bathroom = 2 \times 5 = 10 m^{2}
∴ Area of living room = 180 – (30 \times 2) – 10 – 35 = 75 m^{2}
Ans.5. (b) ₹ 1750
Total cost = 7 m × 5 m × ₹ 50 = ₹ 1750
Case Study Question 13
Read the following and answer any four questions from 1 to 5 given below:
It is common that Governments revise travel fares from time to time based on various factors such as inflation (a general increase in prices and fall in the purchasing value of money) on different types of vehicles like Autos, Rickshaws, Taxis, Radio cabs etc. The Auto charges in a city comprise of a fixed charge together with the charge for the distance covered. Study the following situations: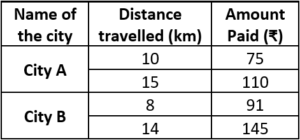
Situation 2: In a city B, for a journey of 8 km, the charge paid is ₹ 91 and for a journey of 14 km, the charge paid is ₹ 145.
Situation 1:
Question.1. If the fixed charges of auto rickshaw be ₹ x and the running charges be ₹ y per km, the pair of linear equations representing the situation is
(a) x + 10y = 110, x + 15y = 75
(b) x + 10y = 75, x + 15y = 110
(c) 10x + y = 110, 15x + y = 75
(d) 10x + y = 75, 15 x + y =110
Question.2. A person travels a distance of 50 km. The amount he has to pay is
(a) ₹ 155
(b) ₹ 255
(c) ₹ 355
(d) ₹ 455
Situation 2:
Question.3. What will a person have to pay for travelling a distance of 30 km?
(a) ₹ 185
(b) ₹ 289
(c) ₹ 275
(d) ₹ 305
Question.4. The graph of lines representing the conditions of both the equations are depicted below. Which one is correct.
(a) 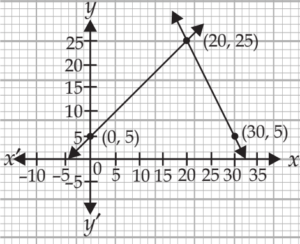
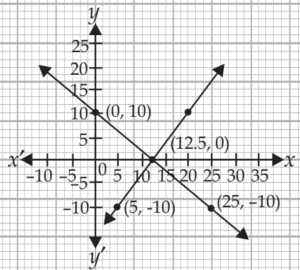
Question.5. Out of both the city, which one has cheaper fare?
(a) City A
(b) City A
(c) Both are same
(d) cannot decided
Ans.1. (b) x + 10y = 75, x + 15y = 110
Ans.2. (c) ₹ 355
Solving equations from (i), we get x=5 and y=7
Now, fare for 50 km = x + 5y = 5 + 50(₹7) = ₹ 355
Ans.3. (b) ₹289
x + 8y = 91 …(i)
x + 14y = 145 …(ii)
Subtracting eq.(ii) from (i), We get
– 6y = – 54
⇒ y = \frac{54}{6}=9
Putting y = 9 in (i), we get x = 19
Now, fare for 30 km = x + 30y = 19 + 30 \times 9 = ₹289
Ans.4. (c) 
Case Study Question 14
Read the following and answer the questions given below:
A man is trying to choose between two phone plans. The first plan of company A, cost ₹ 20 per month, with calls costing an additional 25 paise per minute.
The second plan of company B charges ₹ 40 per month, but calls cost 8 paise per minute. These two situations are shown below which represent linear equations.
The total cost for the two company’s are given by
y = 0.25x + 20 and y = 0.08x + 40
where x is the minutes used and y is the total cost per month.
Question.1. If a person takes first plan and calls for 90 minutes in a month then how much amount he will have to pay whose cost for a month is given by y = 0.25x + 20?
(a) ₹ 20
(b) ₹ 40
(c) ₹ 42.50
(d) ₹ 45
Question.2. Another person takes second plan and also calls for 90 minutes in a month, then the amount which he has to pay when total cost is given by y = 0.08x + 40, is
(a) ₹ 45
(b) ₹ 47
(c) ₹ 45.20
(d) ₹ 47.20
Question.3. Solution of system of linear equations x + 2y = – 1 and 2x – 3y = 12 is
(a) (–3, 2)
(b) (–3, –2)
(c) (3, – 2)
(d) (3, 2)
Question.4. If the system of pair of linear equations kx + 2y = 5, 3x + y = 1 has a unique solution, then
(a) k ≠ \frac{3}{2}
(b) k = 6
(c) k ≠ 6
(d) k ≠ \frac{2}{3}
Question.5. Given system of linear equations x + 2y – 4 = 0, 2x + 4y – 12 = 0 represents
(a) parallel lines
(b) intersecting lines
(c) coincident lines
(d) can’t say
Ans.1. (c)
Ans.2. (d)
Ans.3. (c)
Ans.4. (c)
Ans.5. (a)
Case Study Question 15
Read the following and answer the questions given below:
A cricket bat manufacturer’s revenue is the function used to calculate the amount of money that comes into the business. It can be represented by the equation R = xp, where x = quantity and p = price.
The revenue function is shown in the figure. The cost function is the function used to calculate the costs of doing business. It includes fixed costs, such as rent and salaries, and variable costs such as utilities. The cost function is shown in blue colour in figure.
The x-axis represents quantity (in hundreds) of units, and the y-axis represents either cost or revenue (in thousand of rupees).
The profit function is the difference of revenue function and the cost function, written as
P(x) = R(x) – C(x)
Now, let C(x) = 100x + 30000 and R(x) = 150x
If we replace function by y, we get Linear equations are y = 100x + 30000 and y = 150x
Question.1. The number of bat manufactured (x) so that there is no profit or loss for the manufacturer is
(a) x = 200
(b) x = 300
(c) x = 400
(d) x = 600
Question.2. If the cost and revenue are given by the linear equations y = 0.85x + 35000 and y = 1.55x respectively, and the break-even point is the point at which the two lines intersect, then its break even point is
(a) (50000, 77500)
(b) (50000, 60000)
(c) (45000, 50000)
(d) (45000, 60000)
Question.3. The system of linear equations 3x + 2y = 12, 5x – 2y = 4 represents
(a) parallel lines
(b) intersecting lines
(c) coincident lines
(d) can’t say
Question.4. Solution of the system of linear equations x + y = 1, 2x – 3y = 7, is
(a) (1, 2)
(b) (2, 1)
(c) (2, –1)
(d) (–2, –1)
Question.5. The value of k for which the system of linear equations 4x + 5y = 3 and kx + 15y = 9 has infinitely many solutions is
(a) k = 3
(b) k = 4
(c) k = 12
(d) k = 8
Ans.1. (d)
Ans.2. (a)
Ans.3. (b)
Ans.4. (c)
Ans.5. (c)
Case Study Question 16
Read the following and answer the questions given below:
The scissors which is so common in our daily life use, its blades represent the graph of linear equations.
Let the blades of a scissor are represented by the system of linear equations:
x + 3y = 6 and 2x – 3y = 12
Question.1. The pivot point (point of intersection) of the blades represented by the linear equation x + 3y = 6 and 2x – 3y = 12 of the scissor is
(a) (2, 3)
(b) (6, 0)
(c) (3, 2)
(d) (2, 6)
Question.2. The points at which linear equations x + 3y = 6 and 2x – 3y = 12 intersect y–axis respectively are
(a) (0, 2) and (0, 6)
(b) (0, 2) and (6, 0)
(c) (0, 2) and (0, –4)
(d) (2, 0) and (0, –4)
Question.3. The number of solution of the system of linear equations x + 2y – 8 = 0 and 2x + 4y = 16 is
(a) 0
(b) 1
(c) 2
(d) infinitely many
Question.4. If (1, 2) is the solution of linear equations ax + y = 3 and 2x + by = 12, then values of a and b are respectively
(a) 1, 5
(b) 2, 3
(c) –1, 5
(d) 3, 5
Question.5. If a pair of linear equations in two variables is consistent, then the lines represented by two equations are
(a) intersecting
(b) parallel
(c) always coincident
(d) intersecting or coincident
Ans.1. (b)
Ans.2. (c)
Ans.3. (d)
Ans.4. (a)
Ans.5. (d)
Case Study Question 17
Read the following and answer the questions given below:
A pen stand with a pen is represented by the system of linear equations y = 0 and 3x + 2y = 6.
Question.1. The system of linear equations y = 0 and 3x + 2y = 6 represents the pen stand and a pen respectively then their point of contact (intersection) is
(a) (0, 3)
(b) (2, 0)
(c) (3, 2)
(d) (3, 0)
Question.2. The pair of linear equation y = x and x + y = 6 intersect each other at point
(a) (4, 2)
(b) (4, 4)
(c) (3, 3)
(d) (3, 2)
Question.3. The system of linear equations 3x + 6y = 3900 and x + 3y = 1300 represent the lines which are
(a) parallel
(b) intersecting
(c) coincident
(d) can’t say
Question.4. The value of k for which the system of equations kx – 5y = 2 and 6x + 2y = 7 has no solution, is
(a) 30
(b) –30
(c) 15
(d) –15
Question.5. The linear equation 3x + 2y = 6 intersects the y–axis at the point
(a) (0, 3)
(b) (0, 2)
(c) (0, –3)
(d) (2, 3)
Ans.1. (b)
Ans.2. (c)
Ans.3. (b)
Ans.4. (d)
Ans.5. (a)
Case Study Question 18
Read the following and answer the questions given below:
A boy enjoying the pizza with his friends and share with them by slicing it. During slicing the pizza, he noticed that the pair of linear equations formed.
Let these pair of linear equations be y – 2x = 1 and 5y – x = 14.
Question.1. The point of intersection of the lines given by the equations y – 2x = 1 and 5y – x = 14 is
(a) (–2, 3)
(b) (–4, 2)
(c) (6, 4)
(d) (1, 3)
Question.2. The linear equation y – 2x = 1 intersect the y–axis at point
(a) \left(-\frac{1}{2},0\right)
(b) (0, 1)
(c) (0, –14)
(d) \left(0,\frac{14}{5}\right)
Question.3. The system of linear equations 2x – 3y + 6 = 0 and 2x + 3y – 18 = 0
(a) has a unique solution
(b) has no solution
(c) has infinitely many solution
(d) may or may not have a solution
Question.4. The value(s) of k for which the system of linear equations 2x – ky + 3 = 0 and 3x + 2y – 1 = 0 has no solution, is
(a) \frac{4}{3}
(b) -\frac{4}{3}
(c) 6
(d) –6
Question.5. If a pair of linear equations in two variables is inconsistent, then the lines represented by two equations are
(a) intersecting
(b) parallel
(c) always coincident
(d) Intersecting or coincident
Ans.1. (d)
Ans.2. (b)
Ans.3. (a)
Ans.4. (b)
Ans.5. (b)
Case Study Question 19
Read the following and answer the questions given below:
Special offers are short-term pricing strategies that businesses, especially shops will adopt to encourage customers to buy from them. During winter season, a shopkeeper sells a jacket at 8% profit and a sweater at 10 % discount thereby getting a sum of ₹1008. If she had sold the jacket at 10 % profit and the sweater at 8 % discount, she would have got ₹ 1028. Denoting the cost price of one jacket by ₹ x and the list price of one sweater by ₹ y, answer the following situations.
Question.1. Represent the first situation algebraically.
(a) 12x+10y=11200
(b) 10x+12y=11200
(c) 12x-10y=11200
(d) 10x-12y=1120
Question.2. Represent the second situation algebraically
(a) 46x+55y=51400
(b) 55x+46y=51400
(c) 55x-46y=51400
(d) 46x-55y=51400
Question.3. The system of linear equations representing both the situations will have.
(a) Infinite number of solutions
(b) Unique solution
(c) No Solutions
(d) Exactly two solutions
Question.4. The graph of the system of linear equations representing both the situations will be
(a) Parallel lines
(b) Coincident lines
(c) Intersecting lines
(d) None of these
Let the cost price of one jacket be ₹ x and the list price of one sweater be ₹ y
Ans.1. (a)
According to the first condition,
x+8100x+y-10100 y=1008
108 \times 100+90100y=1008
108x+90y=100800
Dividing through out by 9, we get
12x+10y=11200
Ans.2. (b)
According to the second condition
x+10100x+y-8100 y=1028
110×100+92100y=1028
110x+92y=102800
Dividing through out by 2, we get
55x+46y=51400
Ans.3. (b)
Ans.4. (c)
Case Study Question 20
Read the following and answer the questions given below:
An alumni association is an association of former students. These associations often organize social events, publish newsletters or magazines and raise funds for the organisation. The alumni meet of two batches of a college- batch A & batch B were held on the same day in the same hotel in two separate halls “Rose” and “Jasmine”. The rents were the same for both the halls. The expense for each hall is equal to the fixed rent of each hall and proportional to the number of persons attending each meet. 50 persons attended the meet in “Rose” hall, and the organisers had to pay ₹ 10000 towards the hotel charges. 25 guests attended the meet in “Jasmine” hall and the organisers had to pay ₹ 7500 towards the hotel charges. Denote the fixed rent by ₹ x and proportional expense per person by ₹ y.
Question.1. Represent algebraically the situation in hall “Rose”.
(a) 50x+y=10000
(b) 50x-y=10000
(c) x+50y=10000
(d) x-50y=10000
Question.2. Represent algebraically the situation in hall “Jasmine”
(a) x+25y=7500
(b) x-25y=7500
(c) 25x+y=7500
(d) 25x-y=7500
Question.3. What is the fixed rent of the halls?
(a) ₹ 2500
(b) ₹ 3300
(c) ₹ 4000
(d) ₹ 5000
Question.4. Find the amount the hotel charged per person.
(a) ₹ 150
(b) ₹ 190
(c) ₹ 130
(d) ₹ 100
Let us denote the fixed rent by ₹ x and proportional expense per person by ₹ y.
Ans.1. (c)
Algebraic representation of the situation in “Rose” hall
x+50y=10000
Ans.2. (a)
Algebraic representation of the situation in “Jasmine” hall
x+25y=7500
Subtracting the equations represented by (i) and (ii)
x+50y-x+25y=10000-7500
⇒ 25y=2500
⇒ y=100
Substituting y=100 in x+50y=10000, we get
x+50 \times 100=10000
⇒ x+5000=10000
⇒ x=5000
Ans.3. (d)
Ans.4. (d)
Case Study Question 21
Read the following and answer the questions given below:
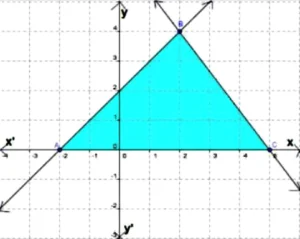
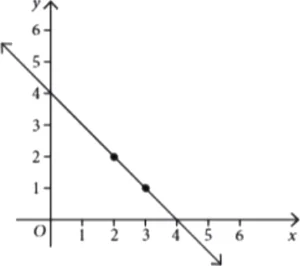
A pair of linear equations is represented geometrically as shown below.
Question.1. What can you say about the pair of linear equations?
(a) Consistent
(b) Inconsistent
(c) Dependent
(d) Cannot be determined
Question.2. From the graph, find the coordinates of the point, where the line AB intersects the x-axis
(a) (5,0)
(b) (-2,0)
(c) (0,2)
(d) (0,0)
Question.3. From the graph, find the solution of the pair of linear equations
(a) (4,2)
(b) (2,4)
(c) (-2,0)
(d) (5,0)
Question.4. What is the area of the shaded region?
(a) 11 sq. units
(b) 12 sq. units
(c) 13 sq. units
(d) 14 sq.units
Ans.1. (a) Consistent
Ans.2. (b) (-2,0)
Ans.3. (b) (2,4)
Ans.4. (d) Area of the shaded region = 12 \times 7 \times 4 = 14 sq. units