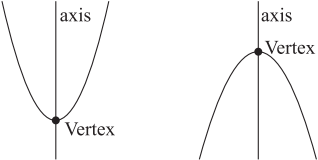
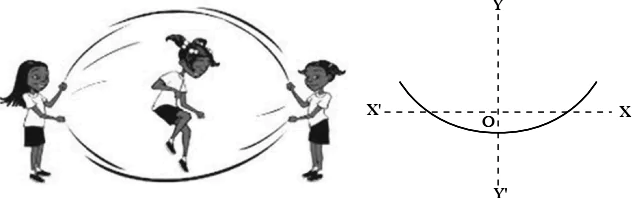What is Case Study Question / Paragraph Based Question?
A case study is a scenario in a particular academic / professional context which students are expected to analyse and respond to, guided by specific questions posed concerning the situation. In many cases, the scenario or case study involves a number of issues or problems that must be dealt with in a academic / professional workplace.
Why Case Study Questions are included in academics?
Case study assignments usually require students to identify problems and issues in a scenario, to demonstrate their developing knowledge of theories and academic / professional policies and to make decisions and recommendations based on these to either prevent or solve some of the issues in that scenario.
How to solve Case Study Questions?
There are several steps to writing an answer to a case study assignment:
STEP 1: Read the case study and questions carefully.
- Read the case and associated questions carefully.
- Highlight the main points of the case and any issues that you can identify.
- Read the questions closely and analyse what they are requiring you to do.
- Read the case again, linking the information that is relevant to each question you have been asked.
STEP 2: Identify the issues in the case study.
Case studies describe a situation which may arise in a particular profession or social context. They often involve a number of people in a complex situation. They will often describe a situation which is problematic, possibly in how it is dealt with, or in its complexity. An important part of your answer is to analyse the situation and to identify the issues/actions described in the case which may be problematic. The following questions may help you to do this:
- What actions were taken in the case?
- Were these actions the most appropriate and why?
- Were there any consequences of the actions taken?
- Was anything omitted or not considered?
- Were actions/procedures in line with existing codes of practice, policy or theories?
STEP 3: Link theory to practice.
Use your knowledge of existing codes of practice, theories and/or other academic / professional documents and behaviours to decide what was done appropriately and what was not.
STEP 4: Plan your answer.
It can be useful to use the questions you have been set as headings and to answer each part in turn, reducing the chance of omitting set questions. You can always take out the headings before you submit if you wish. Lecturers usually set questions in a logical order, so answer in the order they are written in your question.
STEP 5: Start writing your case study answer (for theory only)
Like any assignment, you will need an introduction, body sections in which you answer the questions put to you regarding the case study, and a conclusion.
STEP 6: Edit and proofread.
Read through your paper yourself to detect and correct other errors and omissions.
Check you have answered all questions and backed up your answer with relevant passage.
Types of Case Study Questions / Paragraph Based Questions
Case Study Questions / Paragraph Based Questions can be broadly classified into two types:
- MCQs type: In this type, student has to tick the correct option from various options.
- Theory type: In this type, student has to write proper solution / answer in cotext to the case study.
Case Study/ Passage Based Questions Chapter 8 Introduction to Trigonometry Mathematics
Type 1: MCQ type
Case Study Question 01
Read the following and answer any four questions from 1 to 5 given below:
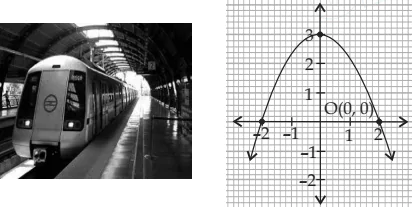
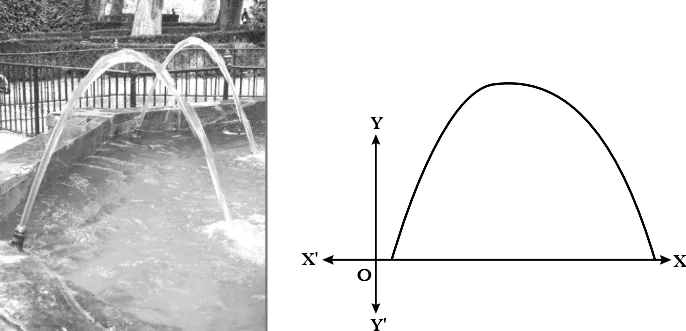
The given pictures are few natural examples of parabolic shape which is represented by a quadratic polynomial. A parabolic arch is an arch in the shape of a parabola. In structures, their curve represents an efficient method of load, and so can be found in bridges and in architecture in a variety of forms.
Question.1. In the standard form of quadratic polynomial, ax^{2}+bx+c , a, b and c are
(a) All are real numbers
(b) All are rational numbers
(c) ‘a’ is a non-zero real number and b & c are any real numbers
(d) All are integers
Question.2. If the roots of the quadratic polynomial are equal, where the discriminant D=b^{2}-4ac , then
(a) D > 0
(b) D < 0
(c) D ≥ 0
(d) D = 0
Question.3. If α and \frac{1}{α} are the zeroes of the qudratic polynomial 2x^{2}-x+8k , then k is
(a) 4
(b) \frac{1}{4}
(c) -\frac{1}{4}
(d) 2
Question.4. The graph of x^{2}+1=0
(a) Intersects x-axis at two distinct points.
(b) Touches x-axis at a point.
(c) Neither touches nor intersects x-axis.
(d) Either touches or intersects x-axis.
Question.5. If the sum of the roots is -p and product of the roots is -\frac{1}{p} , then the quadratic polynomial is
(a) k\left(-px^{2}+\frac{x}{p}+1\right)
(b) k\left(px^{2}-\frac{x}{p}-1\right)
(c) k\left(x^{2}+px-\frac{1}{p}\right)
(d) k\left(x^{2}-px+\frac{1}{p}\right)
Ans.1. (c)
‘a’ is a non-zero real number and b and c are any real numbers.
Ans.2. (d)
D = 0
Ans.3. (b)
We have, 2x^{2}-x+8k
Here a = 2, b = –1 and c = 8k
Now, Product of zeroes = \frac{c}{a}
⇒ α \times \frac{1}{α} = \frac{8k}{2}
∴ k = \frac{1}{4}
Ans.4. (c)
we have, x^{2}+1=0
⇒ x^{2}=-1 (imaginary roots)
Ans.5. (c)
x^{2}-Sx+P=0
⇒ x^{2}-(-p)x+\frac{-1}{p}=0
⇒ x^{2}+px-\frac{1}{p}=0
∴ k\left(x^{2}+px-\frac{1}{p}\right)=0 where k ≠ 0.
Case Study Question 02
Read the following and answer any four questions from 1 to 5 given below:
Seema is studying in class X. She visited the Metro station several times. One day she noticed the roof of the Metro Station. She observed that the roof is formed in a Mathematical shape, that she has learned in Maths class. On reaching home, Seema draws the following graph of the figure:
Question.1. Seema shows the roof of the metro station in which shape?
(a) Spiral
(b) ellipse
(c) linear
(d) Parabola
Question.2. How many zeroes are possible for this shape?
(a) 2
(b) 3
(c) 1
(d) 0
Question.3. In the graph, the zeroes of the polynomial are:
(a) –2, 2
(b) 0, 2
(c) 2, 0
(d) 0, 0
Question.4. What will be the expression of the polynomial?
(a) x^{2}-4x+4
(b) -x^{2}-4x+4
(c) x^{2}+4x+4
(d) x^{2}-4
Question.5. What is the value of the polynomial if x=1 ?
(a) –1
(b) 3
(c) –3
(d) 1
Ans.1. (d)
Parabola
Ans.2. (a)
2
Ans.3. (a)
–2, 2
Ans.4. (d)
Required Polynomial = x^{2}-(α+β)x+αβ
= x^{2}-(-2+2)x+(-2)2
= x^{2}-4
Ans.5. (c)
p(1) = (1)^{2}-4 = –3
Case Study Question 03
Read the following and answer any four questions from 1 to 5 given below:
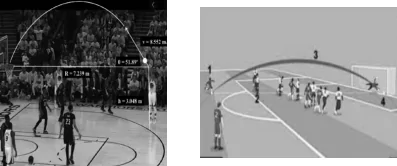
Basketball and soccer are played with a spherical ball. Even though an athlete dribbles the ball in both sports, a basketball player uses his hands and a soccer player uses his feet. Usually, soccer is played outdoors on a large field and basketball is played indoors on a court made of wood. The projectile (path traced) of soccer ball and basketball are in the form of parabola representing quadratic polynomial.
Question.1. The shape of the path traced shown is
(a) Spiral
(b) Ellipse
(c) Linear
(d) Parabola
Question.2. The graph of parabola opens upwards, if ____________ .
(a) a ≥ 0
(b) a = 0
(c) a < 0
(d) a > 0
Question.3. Observe the following graph and answer: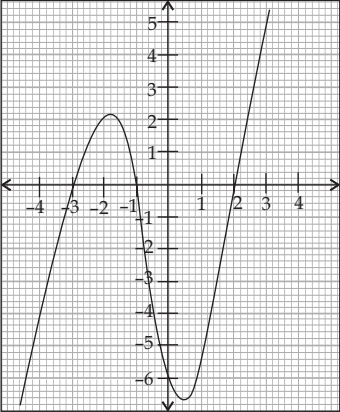
(a) 0
(b) 1
(c) 2
(d) 3
Question.4. The zeroes in the above shown graph are _____________.
(a) 2, 3, –1
(b) –2, 3, 1
(c) –3, –1, 2
(d) –2, –3, –1
Question.5. What will be the expression of the polynomial?
(a) x^{3}+2x^{2}-5x-6
(b) x^{3}+2x^{2}-5x+6
(c) x^{3}+2x^{2}+5x-6
(d) x^{3}+2x^{2}+5x+6
Ans.1. (d)
Parabola
Ans.2. (d)
a > 0
Ans.3. (d)
3
Ans.4. (c)
–3, –1, 2
Ans.5. (a)
As we know, Required cubic polynomial = x^{3}- (sum of zeroes) x^{2}+ (sum of product of two zeroes) x- (product of these zeroes)
= x^{3}-(-3-1+2)x^{2}+[(-3)\times (-1)+(-1) \times 2+2\times (-3)]x-[(-3)\times (-1)\times 2]
= x^{3}+2x^{2}+(3-2-6)x-6
= x^{3}+2x^{2}-5x-6
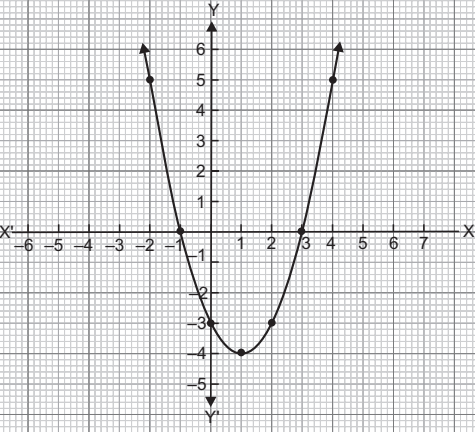
Case Study Question 04
Read the following and answer any four questions from 1 to 5 given below:
An asana is a body posture, originally and still a general term for a sitting meditation pose, and later extended in hatha yoga and modern yoga as exercise, to any type of pose or position, adding reclining, standing, inverted, twisting, and balancing poses. In the figure, one can observe that poses can be related to representation of quadratic polynomial.
Question.1. The graph of x^{2}+1=0
(a) Spiral
(b) Ellipse
(c) Linear
(d) Parabola
Question.2. The graph of parabola opens downwards, if ___________ .
(a) a ≥ 0
(b) a = 0
(c) a < 0
(d) a > 0
Question.3. In the graph, how many zeroes are there for the polynomial?
(a) 0
(b) 1
(c) 2
(d) 3
Question.4. The two zeroes in the above shown graph are
(a) 2, 4
(b) –2, 4
(c) -8, 4
(d) 2, –8
Question.5. The zeroes of the quadratic polynomial are 4\sqrt{3}x^{2}+5x-2\sqrt{3} .
(a) -\frac{2}{\sqrt{3}} , -\frac{\sqrt{3}}{4}
(b) -\frac{2}{\sqrt{3}} , \frac{\sqrt{3}}{4}
(c) \frac{2}{\sqrt{3}} , -\frac{\sqrt{3}}{4}
(d) \frac{2}{\sqrt{3}} , \frac{\sqrt{3}}{4}
Ans.1. (d)
Parabola
Ans.2. (c)
a < 0
Ans.3. (c)
As polynomial graph touches the x–axis at two points.
Ans.4. (b)
–2, 4
Ans.5. (b)
4\sqrt{3}x^{2}+5x-2\sqrt{3}=0
⇒ 4\sqrt{3}x^{2}+8x-3x-2\sqrt{3}=0
⇒ 4x(\sqrt{3}x+2)-\sqrt{3}(\sqrt{3}x+2)=0
⇒ \sqrt{3}x+2=0 or 4x-\sqrt{3}=0
⇒ x=-\frac{2}{\sqrt{3}} or x=\frac{\sqrt{3}}{4}
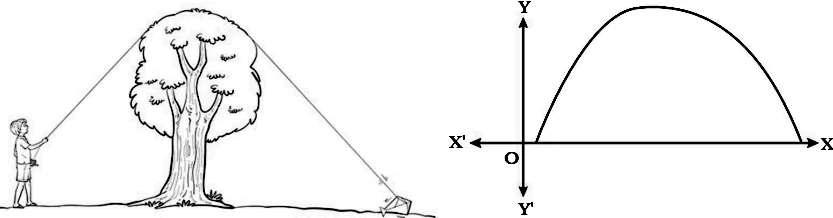
Case Study Question 05
Read the following and answer any four questions from 1 to 5 given below:
A park has swings made of rubber and iron chain. Sachin who is studying in class X has noticed that this is a Mathematical shape, he has learned in Maths class.
Following questions are raised in his mind. Answer the questions by observing both the pictures:
Question.1. Name the shape in which the wire is bent.
(a) Spiral
(b) ellipse
(c) linear
(d) Parabola
Question.2. How many zeroes are there for the polynomial (shape of the wire)?
(a) 2
(b) 3
(c) 1
(d) 0
Question.3. The zeroes of the polynomial are
(a) –1, 5
(b) –1, 3
(c) 3, 5
(d) –4, 2
Question.4. What will be the expression of the polynomial?
(a) x^{2}+2x-3
(b) x^{2}-2x+3
(c) x^{2}-2x-3
(d) x^{2}+2x+3
Question.5. What is the value of the polynomial if x=1 ?
(a) –4
(b) 5
(c) –5
(d) 6
Ans.1. (d)
Parabola
Ans.2. (a)
2
Ans.3. (b)
–1, 3
Ans.4. (c)
As we know, Required Polynomial = x^{2}-(α+β)x+αβ
= x^{2}-(-1+3)x+(-1)3
= x^{2}-2x-3
Ans.5. (a)
p(1)= (1)^{2}-2(1)-3 = 1 – 5 = –4
Case Study Question 06
Read the following and answer any four questions from 1 to 5 given below:
A highway underpass is parabolic in shape.
Question.1. If the highway overpass is represented by x^{2}-2x-8 , then its zeroes are
(a) (2, –4)
(b) (4, –2)
(c) (–2, –2)
(d) (–4, –4)
Question.2. The highway overpass is represented graphically. Zeroes of a polynomial can be expressed graphically. Number of zeroes of polynomial is equal to number of points where the graph of polynomial
(a) intersects x-axis
(b) intersects y-axis
(c) intersects y-axis or x-axis
(d) None of these
Question.3. Graph of a quadratic polynomial is a
(a) straight line
(b) circle
(c) parabola
(d) ellipse
Question.4. The representation of Highway Underpass whose one zero is 6 and sum of the zeroes is 0, is
(a) x^{2}-6x+2
(b) x^{2}-36
(c) x^{2}-6
(d) x^{2}-3
Question.5. The number of zeroes that polynomial f(x)=(x-2)^{2}+4 can have is:
(a) 1
(b) 2
(c) 0
(d) 3
Ans.1. (b)
(4, –2)
Ans.2. (a)
intersects x-axis
Ans.3. (c)
parabola
Ans.4. (b)
x^{2}-36
Ans.5. (c)
0
Case Study Question 07
Read the following and answer any four questions from 1 to 5 given below:
Due to heavy storm an electric wire got bent as shown in the figure. It followed a mathematical shape. Answer the following questions below:
Question.1. Name the shape in which the wire is bent.
(a) spiral
(b) ellipse
(c) linear
(d) parabola
Question.2. How many zeroes are there for the polynomial (shape of the wire)?
(a) 2
(b) 3
(c) 1
(d) 0
Question.3. The zeroes of the polynomial are
(a) –1, 5
(b) –1, 3
(c) 3, 5
(d) –4, 2
Question.4. What will be the expression of the polynomial?
(a) x^{2}+2x-3
(b) x^{2}-2x+3
(c) x^{2}-2x-3
(d) x^{2}+2x+3
Question.5. What is the value of the polynomial if x=-1 ?
(a) 6
(b) –18
(c) 18
(d) 0
Ans.1. (d)
parabola
Ans.2. (a)
2
Ans.3. (b)
-1, 3
Ans.4. (c)
x^{2}-2x-3
Ans.5. (d)
0
Case Study Question 08
Read the following and answer any four questions from 1 to 5 given below:
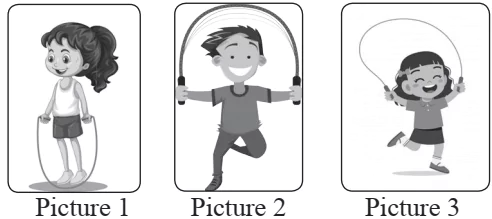
Skipping rope is a good exercise. It burns calories, makes bones strong and improves heart health. During skipping, when rope goes up and down it makes the shape of parabolas (graphs of quadratic polynomials). Observe the following skipping pictures.
Refer Picture 1
Question.1. The graph of polynomial p(x) represented by Picture 1 is shown below.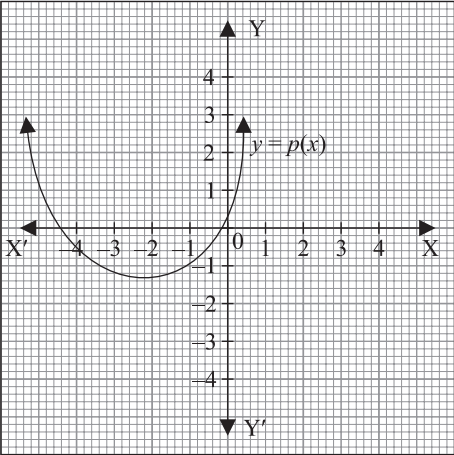
(a) 0
(b) 1
(c) 2
(d) 4
Refer Picture 2
Question.2. The graph of polynomial p(x) represented by Picture 2 is shown below.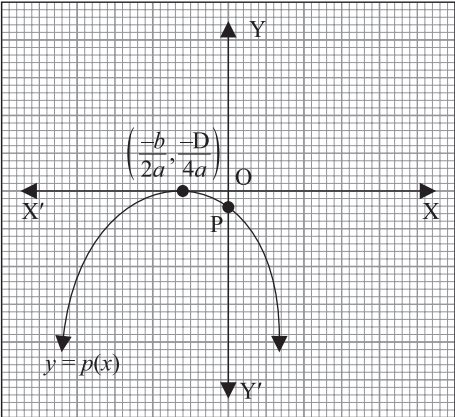
(a) a
(b) b
(c) c
(d) All of these.
Question.3. If \frac{1}{4} and –1 are the sum and product of zeroes of a polynomial whose graph is represented by Picture (3), the quadratic polynomial is
(a) k\left(x^{2}-\frac{1}{4}x-1\right)
(b) k\left(\frac{1}{4}x^{2}-x-1\right)
(c) k\left(x^{2}+\frac{1}{4}x+1\right)
(d) k\left(\frac{1}{4}x^{2}+x+1\right)
Question.4. Let the Picture (1) represents the quadratic polynomial f(x)= x^{2}-8x+k whose sum of the squares of zeroes is 40. The value of k is
(a) 8
(b) 10
(c) 12
(d) 20
Question.5. Let the Picture (3) represents the quadratic polynomial f(x)= x^{2}+7x+10 . Then its zeroes are
(a) –1, –5
(b) –2, –5
(c) 1, 5
(d) 2, 5
Ans.1. (c)
2
Ans.2. (d)
All of these.
Ans.3. (a)
k\left(x^{2}-\frac{1}{4}x-1\right)
Ans.4. (c)
12
Ans.5. (b)
-2, -5
Case Study Question 09
Read the following and answer any four questions from 1 to 4 given below:
Rainbow is an arch of colours that is visible in the sky, caused by the refraction and dispersion of the sun’s light after rain or other water droplets in the atmosphere. The colours of the rainbow are generally said to be red, orange, yellow, green, blue, indigo and violet. Each colour of rainbow makes a parabola. We know that for any quadratic polynomial ax^{2}+bx+c , a ≠ 0, the graph of the corresponding equation y=ax^{2}+bx+c has one of the two shapes either open upwards like ∪ or open downwards like ∩ depending on whether a > 0 or a < 0. These curves are called parabolas.
Question.1. A rainbow is represented by the quadratic polynomial x^{2}+(a+1)x+b whose zeroes are 2 and –3. Then
(a) a = –7, b = –1
(b) a = 5, b = –1
(c) a = 2, b = –6
(d) a = 0, b = –6
Question.2. The polynomial x^{2}-2x-(7p+3) represents a rainbow. If –4 is zero of it, then the value of p is
(a) 1
(b) 2
(c) 3
(d) 4
Question.3. The graph of a rainbow y=f(x) is shown below.
(a) 0
(b) 1
(c) 2
(d) 3
Question.4. If graph of a rainbow does not intersect the x-axis but intersects y-axis in one point, then number of zeroes of the polynomial is equal to
(a) 0
(b) 1
(c) 0 or 1
(d) none of these
Question.5. The representation of a rainbow is a quadratic polynomial. The sum and the product of its zeroes are 3 and –2 respectively. The polynomial is
(a) k(x^{2}-2x-3) , for some real k.
(b) k(x^{2}-5x-9) , for some real k.
(c) k(x^{2}-3x-2) , for some real k.
(d) k(x^{2}-8x+2) , for some real k
Ans.1. (d)
a = 0, b = –6
Ans.2. (c)
3
Ans.3. (c)
2
Ans.4. (a)
0
Ans.5. (c)
k(x^{2}-3x-2) , for some real k.
Case Study Question 10
Read the following and answer any four questions from 1 to 5 given below:
Neeru saw a creeper on the boundary of her aunt’s house which was in the shape as shown in the figure. 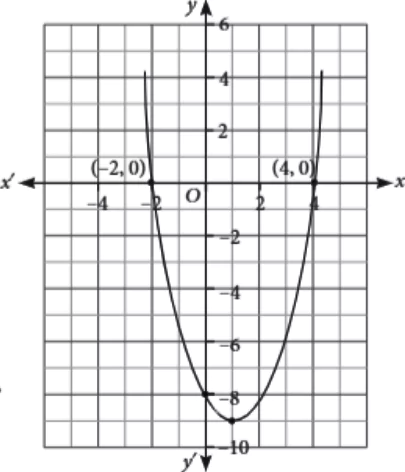
Question.1. The shape represents a _________ polynomial.
(a) Linear
(b) Cubic
(c) Quadratic
(d) None of these
Question.2. How many zeroes does the polynomial (shape of the creeper) have?
(a) 0
(b) 1
(c) 2
(d) 3
Question.3. The zeroes of the polynomial, represented by the graph, are
(a) 4,-2
(b) -4,2
(c) 4,2
(d) -5, 6
Question.4. The expression of the polynomial, represented by the graph, is
(a) x^{2}+2x-8
(b) x^{2}-2x-8
(c) x^{3}-x+8
(d) x^{3}-x^{2}+2x+8
Question.5. For what value of x, the value of the polynomial, represented by the graph, is -5?
(a) x=3
(b) x=-1
(c) Both (a) and (b)
(d) Can’t be determined
Ans.1. (c)
The shape represents a quadratic polynomial.
Ans.2. (c)
Since, the graph of polynomial cuts the x-axis at (-2, 0) and (4, 0). So, the polynomial has 2 zeroes.
Ans.3. (a)
The zeroes of the polynomial are -2 and 4.
Ans.4. (b)
Required polynomial is
p(x) = x^2-(-2+4)x+(-2)(4)
= x^2-2x-8
Ans.5. (c)
Consider, p(x) = -5
⇒ x^{2}-2x-8=-5
⇒ x^{2}-2x-3=0
⇒ (x-3)(x+1)=0
⇒ x=-1 or x=3
Case Study Question 11
Read the following and answer any four questions from 1 to 4 given below:
In a soccer match, the path of the soccer ball in a kick is recorded as shown in the following graph. 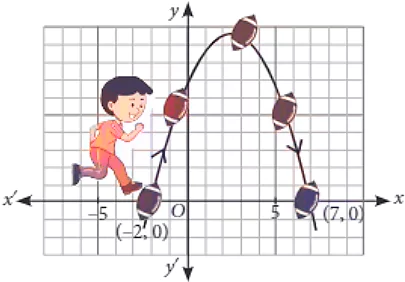
Question.1. The shape of path of the soccer ball is a
(a) Circle
(b) Parabola
(c) Line
(d) None of these
Question.2. The axis of symmetry of the given parabola is
(a) y-axis
(b) x-axis
(c) line parallel to y-axis
(d) line parallel to x-axis
Question.3. The zeroes of the polynomial, represented in the given graph, are
(a) -1,7
(b) 5,-2
(c) -2,7
(d) -3,8
Question.4. Which of the following polynomial has -2 and -3 as its zeroes?
(a) x^{2}-5x-5
(b) x^{2}+5x-6
(c) x^{2}+6x-5
(d) x^{2}+5x+6
Question.5. For what value of x, the value of the polynomial f(x)=(x-3)^{2}+9 is 9?
(a) 1
(b) 2
(c) 3
(d) 4
Ans.1. (b)
The shape of the path of the soccer ball is a parabola.
Ans.2. (c)
The axis of symmetry of the given curve is a line parallel to y-axis.
Ans.3. (a)
The zeroes of the polynomial, represented in the given graph, are -2 and 7, since the curve cuts the x-axis at these points.
Ans.4. (d)
A polynomial having zeroes -2 and -3 is p(x) = x^{2}-(-2-3)x+(-2)(-3)= x^{2}+5x+6
Ans.5. (c)
We have, f(x) = (x−3)^{2}+9
Now, 9=(x−3)^{2}+9
⇒ (x−3)^{2}=0
⇒ x−3=0
⇒ x=3
Case Study Question 12
Read the following and answer any four questions from 1 to 5 given below:
Prachi was playing with a slinky spring dog toy and asked her brother Rhythm, what is the shape thus formed called. Rhythm explained her that the shape formed is a parabola. He also explained her that parabola is the graphical representation of a quadratic polynomial. Based on the above information, answer the following questions.
Question.1. The general form of polynomial representing the parabolic graph is
(a) ax^{2}+c, a \neq 0
(b) ax^{2}+bx+c, b \neq 0
(c) ax^{2}+bx+c, a, b and c \neq 0
(d) ax^{2}+bx+c, a \neq 0
Question.2. Kavita drawn a parabola passing through (-4, 3), (−1, 0), (1, 8), (0, 3), (-3, 0) and (-2, -1) on the graph paper. Then zeroes of the polynomial representing the graph is
(a) 3 and -3
(b) -1 and -2
(c) -3 and -1
(d) 1 and 8
Question.3. Which of the following is correct?
(a) A parabola intersects x-axis at maximum 2 points.
(b) A parabola intersects x-axis only at 1 point.
(c) A parabola intersects x-axis exactly at 2 points.
(d) A parabola intersects x-axis at least at 2 points.
Question.4. The product of roots of the polynomial 5x(x-6) is
(a) \frac{3}{2}
(b) \frac{2}{3}
(c) 3
(d) 0
Question.5. The sum of zeroes of a quadratic polynomial ax^{2}+bx+c, a \neq 0 is
(a) \frac{a}{b}
(b) \frac{a}{c}
(c) \frac{-b}{a}
(d) \frac{-c}{a}
Ans.1. (d)
The general form of polynomial representing the parabolic graph is ax^{2}+bx+c, a \neq 0.
Ans.2. (c)
The zeroes of the polynomial are the points at which its graph intersects the x-axis, i.e., whose y coordinate is 0. Therefore, Zeroes are -3 and -1.
Ans.3. (a) A parabola intersects x-axis at maximum 2 points.
Ans.4.(d)
The product of roots of the polynomial 5x^{2}-30x is 0.
[because Constant term = 0]
Ans.5. (c)
Sum of zeroes of quadratic polynomial ax^{2}+bx+c, a \neq 0 is \frac{-b}{a}.
Case Study Question 13
Read the following and answer any four questions from 1 to 5 given below:
Highway Tunnel
Shweta and her husband Sunil who is an architect by profession, visited France. They went to see Mont Blanc Tunnel which is a highway tunnel between France and Italy, under the Mont Blanc Mountain in the Alps, and has a parabolic cross-section. The mathematical representation of the tunnel is shown in the graph. Based on the above information, answer the following questions.
Question.1. The zeroes of the polynomial whose graph is given, are
(a) -2, 8
(b) -2, -8
(c) 2, 8
(d) -2, 0
Question.2. What will be the expression of the polynomial given in diagram?
(a) x^{2}-6x+16
(b) -x^{2}+6x+16
(c) x^{2}+6x+16
(d) -x^{2}-6x-16
Question.3. What is the value of the polynomial, represented by the graph, when x=4?
(a) 22
(b) 23
(c) 24
(d) 25
Question.4. If the tunnel is represented by -x^{2}+3x-2, then its zeroes are
(a) -1, -2
(b) 1, -2
(c) -1, 2
(d) 1, 2
Question.5. If one zero is 4 and sum of zeroes is -3, then representation of tunnel as a polynomial is
(a) x^{2}-x+24
(b) -x^{2}-3x+28
(c) x^{2}+x+28
(d) x^{2}-x+28
Ans.1. (a)
Since, the graph intersects the x-axis at two points, namely x=8, -2.
So, 8, -2 are the zeroes of the given polynomial.
Ans.2. (b)
The expression of the polynomial given in diagram is -x^{2}+6x+16.
Ans.3. (c)
Let p(x)=-x^{2}+6x+16
When x=4, p(4)=-(4)^{2}+6(4)+16=24.
Ans.4. (d)
Let f(x)=-x^{2}+3x-2
Now, consider f(x)=0
⇒ -x^{2}+3x-2=0
⇒ x^{2}-3x+2=0
⇒ (x-2)(x-1)=0
⇒ x=1,2 are its zeroes.
Ans.5. (b)
Let α and β are the zeroes of the required polynomial.
Given, α + β = -3
If α = 4, then β = -7
therefore Representation of tunnel is -x^{2}-3x+28.
Case Study Question 14
Read the following and answer the questions given below:
Architectural Structures
Quadratic polynomial can be used to model the shape of many architectural structures in the world. Pershing field of Jersey city in US is one such structure. Based on the above information, answer the following questions.
Question.1. If the Arch is represented by 10x^{2}-x-3, then its zeroes are
(a) \frac{1}{2}, \frac{-3}{2}
(b) \frac{-1}{2}, \frac{3}{5}
(c) \frac{-1}{2}, \frac{1}{3}
(d) \frac{-1}{3}, \frac{2}{3}
Question.2. The zeroes of the polynomial are the points where its graph
(a) intersect the x-axis
(b) intersect the y-axis
(c) intersect either of the axes
(d) Can’t say
Question.3. The quadratic polynomial whose sum of zeroes is 0 and product of zeroes is 1 is given by
(a) x^{2}-x
(b) x^{2}+x
(c) x^{2}-1
(d) x^{2}+1
Question.4. Which of the following has \frac{1}{2} and 2 as their zeroes?
(a) 6x^{2}-4x+6
(b) 3x^{2}-x+2
(c) 2x^{2}-7x+2
(d) 2x^{2}-3x-2
Question.5. The product of zeroes of the polynomial \sqrt{3}x^{2}-14x+8\sqrt{3} is
(a) 4
(b) 6
(c) 8
(d) 10
Case Study Question 15
Read the following and answer the questions given below:
Priya visited a temple in Gwalior. On the way she sees the Agra Fort. The entrance gate of the fort has a shape of quadratic polynomial (parabolic). The mathematical representation of the gate is shown in the figure. Based on the above information, answer the following questions.
Question.1. Find the zeroes of the polynomial represented by the graph.
(a) -1,3
(b) 1,3
(c) 1,-3
(d) 0,1
Question.2. What will be the expression for the polynomial represented by the graph?
(a) x^{2}+4x-5
(b) x^{2}-4x+5
(c) -x^{2}+4x-3
(d) x^{2}+5x-4
Question.3. What will be the value of polynomial, represented by the graph, when x=4?
(a) -2
(b) 3
(c) -3
(d) 2
Question.4. If one zero of a polynomial p(x) is 7 and product of its zeroes is -35, then p(x)=
(a) -x^{2}+2x+35
(b) x^{2}+2x+35
(c) x^{2}+12x-35
(d) x^{2}-12x-35
Question.5. If the gate is represented by the polynomial -x^{2}+5x-6, then its zeroes are
(a) 2,-3
(b) 2,3
(c) -2,3
(d) -2,-3
Case Study Question 16
Read the following and answer the questions given below:
Social Service
Shray, who is a social worker, wants to distribute masks, gloves, and hand sanitizer bottles in his block. Number of masks, gloves and sanitizer bottles distributed in 1 day can be represented by the zeroes α, β, γ, (α > β > γ) of the polynomial p(x)=x^{3}-18x^{2}+95x-150. Based on the above information, answer the following questions.
Question.1. Find the value of α, β, γ.
(a) -10, -5, -3
(b) 3, 6, 5
(c) 10, 5, 3
(d) 4, 8, 9
Question.2. The sum of product of zeroes taken two at a time is
(a) 91
(b) 92
(c) 94
(d) 95
Question.3. Product of zeroes of polynomial p(x) is
(a) 150
(b) 160
(c) 170
(d) 180
Question.4. The value of the polynomial p(x), when x=4 is
(a) 5
(b) 6
(c) 7
(d) 8
Question.5. If α, β, γ are the zeroes of a polynomial g(x) such that α + β + γ = 3, αβ + βγ + γα = -16 and αβγ =-48, then g(x)=
(a) x^{3}-2x^{2}-48x+6
(b) x^{3}+3x^{2}+16x-48
(c) x^{3}-48x^{2}-16x+3
(d) x^{3}-3x^{2}-16x+48
Case Study Question 17
Read the following and answer the questions given below:
Barrier Chains
While playing badminton Ronit seeing the barrier chains hung between two posts at the edge of the walk way of a street. It is hung in the shape of the parabola. Parabola is the graphical representation of a particular type of polynomial. Based on the above information, answer the following questions.
Question.1. Which of the following polynomial is graphically represented by a parabola?
(a) Linear polynomial
(b) Quadratic polynomial
(c) Cubic polynomial
(d) None of these
Question.2. If a polynomial, represented by a parabola, intersects the x-axis at -3, 4 and y-axis at -2, then its zero(es) is/are
(a) -1, 2 and -2
(b) 2 and -2
(c) -1
(d) -3 and 4
Question.3. If the barrier chains between two posts is represented by the polynomial x^{2}-x-12, then its zeroes are
(a) 4, 3
(b) -2, 5
(c) 4, -3
(d) 4, -5
Question.4. The sum of zeroes of the polynomial 4x^{2}-9x+2 is
(a) \frac{1}{4}
(b) \frac{9}{4}
(c) \frac{2}{4}
(d) \frac{-9}{4}
Question.5. The reciprocal of product of zeroes of the polynomial x^{2}-9x+20 is
(a) 5
(b) \frac{1}{8}
(c) \frac{1}{20}
(d) 20
Ans.1. (b)
Ans.2. (d)
Since, the parabola intersects the x-axis at -3 and 4. So, zeroes of the polynomial are -3 and 4.
Ans.3. (c)
Let f(x)=x^{2}-x-12
= x^{2}-4x+3x-12
= (x+3)(x-4)
Consider f(x)=0
⇒ (x+3)(x-4)=0
⇒ x=4,-3
Ans.4. (b)
Sum of zeroes = -\frac{coefficient of x}{Coefficient of x^{2}}
= -\frac{(-9)}{4}
= \frac{9}{4}
Ans.5. (c): Product of zeroes = \frac{20}{1} = 20
∴ Reciprocal of product of zeroes = \frac{1}{20}
Case Study Question 18
Read the following and answer the questions given below:
Painting Exhibition
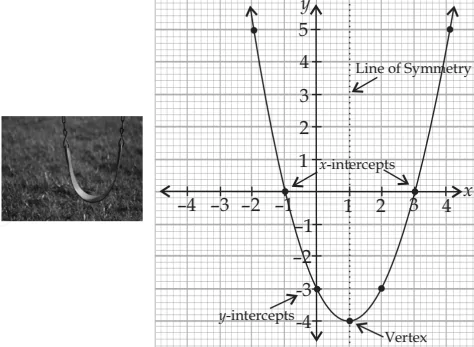
Shruti is very good in painting. So she thought of exhibiting her paintings in which she want to display her latest painting which is in the form of a graph of a polynomial as shown below: Based on the above information, answer the following questions.
Question.1. The number of zeroes of the polynomial represented by the graph is
(a) 1
(b) 2
(c) 3
(d) can’t be determined
Question.2. The sum of zeroes of the polynomial represented by the graph is
(a) -4
(b) -3
(c) 2
(d) -5
Question.3. Find the value of the polynomial represented by the graph when x=0.
(a) -6
(b) -8
(c) 6
(d) 8
Question.4. The polynomial representing the graph drawn in the painting by Shruti is a
(a) quadratic polynomial
(b) cubic polynomial
(c) bi-quadratic polynomial
(d) linear polynomial
Question.5. The sum of product of zeroes, taken two at a time, of the polynomial represented by the graph is
(a) 2
(b) 3
(c) -2
(d) -3
Ans.1. (c)
Since the graph intersect the x-axis at 3 points, therefore the polynomial has 3 zeroes.
Ans.2. (d)
Clearly the graph intersect the x-axis at x=-4, x=-2 and x=1, therefore the zeroes are -4, -2 and 1.
Now, the sum of zeroes = -4 -2 + 1 = -5
Ans.3. (b)
From the graph, it can be seen that When x=0, then y=-8.
Ans.4. (b)
Since there are 3 zeroes, therefore the graph represents a cubic polynomial.
Ans.5. (a)
The sum of product of zeroes taken two at a time = (-4)(-2) + (−2)(1) + (1)(-4) = 8-2-4 = 2
Case Study Question 19
Read the following and answer the questions given below:
Construction of Humps
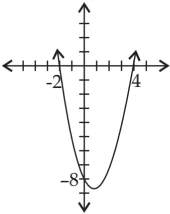
ABC construction company got the contract of making speed humps on roads. Speed humps are parabolic in shape and prevents overspeeding, minimise accidents and gives a chance for pedestrians to cross the road. The mathematical representation of a speed hump is shown in the given graph. Based on the above information, answer the following questions.
Question.1. The polynomial represented by the graph can be _________ polynomial.
(a) Linear
(b) Quadratic
(c) Cubic
(d) Zero
Question.2. The zeroes of the polynomial represented by the graph are
(a) 1, 5
(b) 1, -5
(c) -1, 5
(d) -1, -5
Question.3. The sum of zeroes of the polynomial represented by the graph are
(a) 4
(b) 5
(c) 6
(d) 7
Question.4. If α and β are the zeroes of the polynomial represented by the graph such that β > α, then │8α + β│=
(a) 1
(b) 2
(c) 3
(d) 4
Question.5. The expression of the polynomial represented by the graph is
(a) -x^{2}-4x-5
(b) x^{2}+4x+5
(c) x^{2}+4x-5
(d) -x^{2}+4x+5
Ans.1. (b)
Since, the given graph is parabolic is shape, therefore it will represent a quadratic polynomial. [because Graph of quadratic polynomial is parabolic in shape].
Ans.2. (c)
Since, the graph cuts the x-axis at -1, 5. So the polynomial has 2 zeroes i.e., -1 and 5.
Ans.3. (a)
Sum of zeroes = -1+5 = 4
Ans.4. (c)
Since α and β are zeroes of the given polynomial and β > α.
∴ α = -1 and β = 5.
∴ |8α + β| = |8(-1)+5| = |−8+5| = |-3| = 3.
Ans.5. (d)
∵ the zeroes of the given polynomial are – 1 and 5.
∴ Required polynomial p(x)=k{x^{2}-(-1+5)x+(−1)(5)} = k(x^{2}-4x-5)
For k = -1, we get
p(x)=-x^{2}+4x+5, which is the required polynomial.
Case Study Question 20
Read the following and answer the questions given below:
Honeycomb
While playing in garden, Sahiba saw a honeycomb and asked her mother what is that. She replied that it’s a honeycomb made by honey bees to store honey. Also, she told her that the shape of the honeycomb formed is parabolic. The mathematical representation of the honeycomb structure is shown in the graph. Based on the above information, answer the following questions.
Question.1. Graph of a quadratic polynomial is ___________ in shape.
(a) straight line
(b) parabolic
(c) circular
(d) None of these
Question.2. The expression of the polynomial represented by the graph is
(a) x^{2}-49
(b) x^{2}-64
(c) x^{2}-36
(d) x^{2}-81
Question.3. Find the value of the polynomial represented by the graph when x=6.
(a) -2
(b) -1
(c) 0
(d) 1
Question.4. The sum of zeroes of the polynomial x^{2}+2x-3 is
(a) -1
(b) -2
(c) 2
(d) 1
Question.5. If the sum of zeroes of polynomial at^{2}+5t+3a is equal to their product, then find the value of a.
(a) -5
(b) -3
(c) \frac{5}{3}
(d) \frac{-5}{3}
Ans.1. (b)
Graph of a quadratic polynomial is a parabolic in shape.
Ans.2. (c)
Since the graph of the polynomial cuts the x-axis at (-6, 0) and (6, 0). So, the zeroes of polynomial are -6 and 6.
therefore Required polynomial is
p(x)=x^{2}-(-6+6)x+(−6)(6)
= x^{2}-36
Ans.3. (c)
We have, p(x)=x^{2}-36
Now, p(6)=6^{2}-36
=36-36
=0
Ans.4. (b)
Let f(x)=x^{2}+2x-3. Then,
Sum of zeroes = {-\frac{coefficient of x}{coefficient of x^{2}}}
=-\frac{2}{1}
=-2
Ans.5. (d)
The given polynomial is at^{2}+5t+3a
Given, sum of zeroes = product of zeroes
\frac{-5}{a} =\frac{3a}{a}
⇒ a=\frac{-5}{3}
Case Study Question 21
Read the following and answer the questions given below:
Just before the morning assembly a teacher of kindergarten school observes some clouds in the sky and so she cancels the assembly. She also observes that the clouds has a shape of the polynomial. The mathematical representation of a cloud is shown in the figure.
Question.1. Find the zeroes of the polynomial represented by the graph.
(a) \frac{-1}{2}, \frac{7}{2}
(b) \frac{1}{2}, \frac{-7}{2}
(c) \frac{-1}{2}, \frac{-7}{2}
(d) \frac{1}{2}, \frac{7}{2}
Question.2. What will be the expression for the polynomial represented by the graph?
(a) p(x)=12x^{2}-4x-7
(b) p(x)=x^{2}-12x+3
(c) p(x)=4x^{2}+12x+7
(d) p(x)=-4x^{2}-12x+7
Question.3. What will be the value of polynomial represented by the graph, when x=3?
(a) 65
(b) -65
(c) 68
(d) -68
Question.4. If α and β are the zeroes of the polynomial f(x)=x^{2}+2x-8, then α^{4}+β^{4}=
(a) 262
(b) 252
(c) 272
(d) 282
Question.5. Find a quadratic polynomial where sum and product of its zeroes are 0, \sqrt{7} respectively.
(a) k(x^{2}+\sqrt{7})
(b) k(x^{2}-\sqrt{7})
(c) k(x^{2}+\sqrt{5})
(d) none of these
Ans.1. (b)
Since the graph of the polynomial intersect the x-axis at x=\frac{1}{2}, \frac{-7}{2}, therefore required zeroes of the polynomial are \frac{1}{2} and \frac{-7}{2}.
Ans.2. (d)
because \frac{1}{2} and \frac{-7}{2} are the zeroes of the polynomial.
So, at x=\frac{1}{2}, \frac{-7}{2}, the value of the polynomial will be 0.
From options, required polynomial is p(x)=-4x^{2}-12x+7.
Ans.3. (b)
We have, p(x)=-4x^{2}-12x+7.
therefore p(3) = -4(3)^{2}-12(3)+7
= – 36 – 36 + 7
= – 65
Ans.4. (c)
Here f(x) = x^{2}+ 2x – 8 and α, β are its zeroes.
therefore α + β = -2 and αβ = -8
Now, α^{4}+β^{4} = (α^{2}+β^{2})^{2}-2α^{2}β^{2}
= ((α+β)^{2}-2αβ)^{2}-2(αβ)^{2}
= ((-2)^{2}-2(-8))^{2}-2(-8)^{2}
= (4+16)^{2}-2(-8)^{2}
= (20)^{2}-2(64)
= 400 – 128
= 272
Ans.5. (a)
We have sum of zeroes = 0 and product of zeroes = \sqrt{7}
So, required polynomial = k(x^{2}-(0)x+\sqrt{7})
= k(x^{2}+\sqrt{7})
Case Study Question 22
Read the following and answer the questions given below:
Pankaj’s father gave him some money to buy avocado from the market at the rate of p(x)=x^{2}-24x+128. Let α, β are the zeroes of p(x). Based on the above information, answer the following questions.
Question.1. Find the value of α and β, where α < β.
(a) -8, -16
(b) 8, 16
(c) 8, 15
(d) 4, 9
Question.2. Find the value of α + β + αβ.
(a) 151
(b) 158
(c) 152
(d) 155
Question.3. The value of p(2) is
(a) 80
(b) 81
(c) 83
(d) 84
Question.4. If α and β are zeroes of x^{2}+x-2, then \frac{1}{α}+\frac{1}{β}=
(a) \frac{1}{2}
(b) \frac{1}{3}
(c) \frac{1}{4}
(d) \frac{1}{5}
Question.5. If sum of zeroes of q(x)=kx^{2}+2x+3k is equal to their product, then k=
(a) \frac{2}{3}
(b) \frac{1}{3}
(c) \frac{-2}{3}
(d) \frac{-1}{3}
Ans.1. (b) Given, α and β are the zeroes of p(x) = x^{2}-24x+128.
Putting p(x) = 0, we get
x^{2}-8x-16x+128=0
⇒ x(x-8)-16(x-8)=0
⇒ (x-8)(x-16)=0
⇒ x=8 or x=16
⇒ α = 8, β = 16
Ans.2. (c)
⇒ α + β + αβ = 8 + 16 + (8)(16)
= 24 + 128
= 152
Ans.3. (d)
⇒ p(2) = 2^{2}-24(2)+128
= 4 – 48 + 128
= 84
Ans.4. (a)
∵ α and β are zeroes of x^{2}+x-2.
∴ α + β = -1 and αβ = -2
Now, \frac{1}{α}+\frac{1}{β} = \frac{β +α}{α β} = \frac{-1}{-2} =\frac{1}{2}
Ans.5. (c)
Sum of zeroes = \frac{-2}{k}
Product of zeroes = \frac{3k}{k} = 3
According to question, we have \frac{-2}{k} = 3
⇒ k=\frac{-2}{3}
Case Study Question 23
Read the following and answer the questions given below:
Mountain Trekking
Two friends Trisha and Rohan during their summer vacations went to Manali. They decided to go for trekking. While trekking they observes that the trekking path is in the shape of a parabola. The mathematical representation of the track is shown in the graph. Based on the above information, answer the following questions.
Question.1. The zeroes of the polynomial whose graph is given, are
(a) 4,7
(b) -4,7
(c) 4,3
(d) 7, 10
Question.2. What will be the expression of the given polynomial p(x)?
(a) x^{2}-3x+28
(b) -x^{2}+4x+28
(c) x^{2}-4x+28
(d) -x^{2}+3x+28
Question.3. Product of zeroes of the given polynomial is
(a) -28
(b) 28
(c) -30
(d) 30
Question.4. The zeroes of the polynomial 9x^{2}-5 are
(a) \frac{3}{\sqrt{5}}, \frac{-3}{\sqrt{5}}
(b) \frac{2}{\sqrt{5}}, \frac{-2}{\sqrt{5}}
(c) \frac{\sqrt{5}}{3}, \frac{-\sqrt{5}}{3}
(d) \frac{\sqrt{5}}{2}, \frac{-\sqrt{5}}{2}
Question.5. If f(x)=x^{2}-13x+1, then f(4)=
(a) 35
(b) -35
(c) 36
(d) -36
Ans.1. (b)
Since, the graph intersects the x-axis at two points, namely x = -4, 7
So, -4, 7 are the zeros of the polynomial.
Ans.2. (d)
p(x) = -x^{2}+3x+28
Ans.3. (a)
Product of zeroes = \frac{Constant term}{Coefficient of x^{2}}
∴ Required product of zeroes = \frac{28}{-1} = -28
Ans.4. (c)
We have, 9x^{2}-5=(3x)^{2}-(\sqrt{5})^{2}
= (3x-\sqrt{5})(3x+\sqrt{5})
∴ x= \frac{\sqrt{5}}{3} or \frac{-\sqrt{5}}{3}
Ans.5. (b)
Here, f(x) = x^{2}-13x+1
∴ f(4) = 4^{2}-13(4)+1
= 16 – 53 + 1
= -35
Case Study Question 24
Read the following and answer the questions given below:
The tutor in a coaching centre was explaining the concept of cubic polynomial as – A cubic polynomial is of the form ax^{3}+bx^{2}+cx+d, a \neq 0 and it has maximum three real zeroes. The zeroes of a cubic polynomial are namely the x-coordinates of the points where the graph of the polynomial intersects the x-axis. If α, β and γ are the zeroes of a cubic polynomial ax^{3}+bx^{2}+cx+d, then the relation between their zeroes and their coefficients are α + β + γ =\frac{-b}{a}, αβ + βγ + γα =\frac{c}{a} and αβγ =\frac{-d}{a}.
Based on the above information, answer the following questions.
Question.1. Which of the following are the zeroes of the polynomial x^{3}-4x^{2}-7x+10?
(a) -3, 1 and 3
(b) -1, 2 and -3
(c) 2, -1 and 5
(d) -2, 1 and 5
Question.2. If -2 and 5 are zeroes of a cubic polynomial, then the sum of product of zeroes taken two at a time is
(a) \frac{23}{2}
(b) -23
(c) \frac{-1}{2}
(d) \frac{-23}{2}
Question.3. In which of the following polynomials the sum and product of zeroes are equal?
(a) x^{3}-x^{2}+5x-1
(b) x^{3}-4x
(c) 3x^{3}-5x^{2}-11x-3
(d) Both (a) and (b)
Question.4. The polynomial whose all the zeroes are same is
(a) x^{3}+x^{2}+x-1
(b) x^{3}-3x^{2}+3x-1
(c) x^{3}-5x^{2}+6x-1
(d) 3x^{3}+x^{2}+2x-1
Question.5. The cubic polynomial, whose graph is as shown below, is
(a) x^{3}-5x^{2}+8x-4
(b) 3x^{3}-4x^{2}+x-5
(c) x^{3}-7x^{2}+11x+9
(d) x^{3}-9
Ans.1. (d)
For finding zeros, check whether
x^{3}-4x^{2}-7x+10 is zero for given zeros.
Let p(x)=x^{3}-4x^{2}-7x+10. Then
Clearly p(-2)=p(1)=p(5)=0
So, the zeros are -2, 1 and 5.
Ans.2. (d)
Here, α = \frac{-1}{2}, β = -2 and γ = 5
∴ Sum of product of zeroes taken two at a time = αβ+βγ+γα
= \frac{-1}{2} (-2)+(-2)(5)+(5)\frac{-1}{2}
= 1-10-\frac{5}{2}
= -\frac{23}{2}
Ans.3. (d)
Consider x^{3}-x^{2}+5x-1
Sum of zeroes = 1 = Product of zeroes
Now, consider x^{3}-4x
Sum of zeroes = 0 = Product of zeroes
Ans.4. (b)
Let α, α, α be the zeroes of the cubic polynomial. [∵ All zeroes are same]
Then α^{3}= 1
⇒ α = 1 [Using given options]
So, the required polynomial is (x-1)^{3} = x^{3}-3x^{2}+3x-1
Ans.5. (a)
Clearly x = 1 and x = 2 are the zeroes of the given polynomial, both of which satisfies x^{3}-5x^{2}+8x-4.
Case Study Question 25
Read the following and answer any four questions from 1 to 5.
The wall of room is decorated with beautiful garlands, each garland forming a parabola.
Question.1. What type of polynomial does a parabola represent?
(a) linear
(b) quadratic
(c) cubic
(d) None of these
Question.2. The number of zeros of a quadratic polynomial is
(a) equal to 2
(b) equal to 1
(c) more than 2
(d) atmost 2
Question.3. A quadratic polynomial with the sum and product of its zeroes as –1 and –2 is
(a) x^{2}+x-2
(b) x^{2}-x-2
(c) x^{2}+2x-1
(d) x^{2}-2x-1
Question.4. If one of the zeroes of the quadratic polynomial (k-2)x^{2}-2x-5 is –1, then the value of k is
(a) 3
(b) 5
(c) –5
(d) –3
Question.5. If a b , are the zeros of the polynomial f(x)=x^{2}-7x+12 then the value of \frac{1}{α}+\frac{1}{β} is
(a) –7
(b) 12
(c) \frac{7}{12}
(d) \frac{-7}{12}
Ans.1. (b)
Ans.2. (d)
Ans.3. (a)
Ans.4. (b)
Ans.5. (c)
Case Study Question 26
Read the following and answer any four questions from 1 to 5.
Water flowing in a fountain follows trajectory as shown below:
Question.1. The shape formed by the water trajectory is
(a) ellipse
(b) oval
(c) parabola
(d) spiral
Question.2. Number of zeroes of polynomial is equal to the number of points where the graph of polynomial
(a) intersects x– axis
(b) intersects y– axis
(c) intersects y– axis or x– axis
(d) none of the above
Question.3. If the trajectory is represented by x^{2}-3x-18 , then its zeros are
(a) (6, – 3)
(b) (–6, 3)
(c) (3, – 3)
(d) (–6, –3)
Question.4. If \frac{-1}{3} is one of the zeroes of 9x^{2}-kx-9, then the value of k is
(a) 9
(b) 3
(c) 12
(d) 4
Question.5. If α and β are the roots of the equation 2x^{2}-3x-5 then α+β is equal to
(a) 3
(b) –3
(c) \frac{-3}{2}
(d) \frac{3}{2}
Ans.1. (c)
Ans.2. (a)
Ans.3. (a)
Ans.4. (c)
Ans.5. (d)
Case Study Question 27
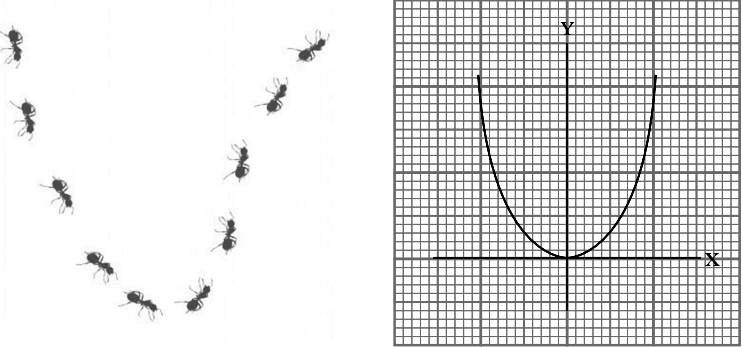
Read the following and answer any four questions from 1 to 5.
The path moved by a group of ants has been traced on a floor which is shown below:
Question.1. The shape formed by the path is
(a) ellipse
(b) oval
(c) parabola
(d) spiral
Question.2. If the path is represented by x^{2}+2x-3 , then its zeroes are
(a) (–3, 1)
(b) (3, –1)
(c) (2, –3)
(d) (–2, 3)
Question.3. The number of zeroes of the polynomial represented by the path is
(a) one
(b) at most two
(c) atleast two
(d) less than two
Question.4. If the sum and product of zeroes of the polynomial representing the path are 6 and –16, then the polynomial is
(a) x^{2}-10x+96
(b) x^{2}-6x+16
(c) x^{2}-6x-16
(d) x^{2}+6x
Question.5. The number of zeroes of the polynomial f(x)=x^{2}-8 are
(a) 0
(b) 1
(c) 2
(d) 3
Ans.1. (c)
Ans.2. (a)
Ans.3. (b)
Ans.4. (c)
Ans.5. (c)
Case Study Question 28
Read the following and answer any four questions from 1 to 5.
A runner is running along a straight path parallel to a given boundary.
Question.1. The path of the runner represents the graph of a
(a) cubic polynomial
(b) quadratic polynomial
(c) linear polynomial
(d) None of these
Question.2. The equation of this graph can be written as
(a) x = 2
(b) y = 2
(c) x = 0
(d) y = 0
Question.3. How many zeros does it have?
(a) 0
(b) 1
(c) 2
(d) more than 1
Question.4. If the graph would have been parallel to x-axis, then its number of zeroes would be
(a) 0
(b) 1
(c) 2
(d) more than 1
Question.5. If one zero of the polynomial p(z)=3z^{2}-10z+m is reciprocal of other, then value of m is
(a) 2
(b) 3
(c) 5
(d) 6
Ans.1. (c)
Ans.2. (a)
Ans.3. (b)
Ans.4. (a)
Ans.5. (b)
Case Study Question 29
Read the following and answer any four questions from 1 to 5.
A child was flying a kite, and its string got struck into a tree and touched ground as shown in figure.
Question.1. The string of the kite represents the graph of a
(a) linear polynomial
(b) quadratic polynomial
(c) cubic polynomial
(d) polynomial of degree more than
Question.2. The number of zeros of a cubic polynomial is
(a) 2
(b) atmost 2
(c) 3
(d) atmost 3
Question.3. If one zero of the polynomial x^{2}-12x+(3k-1) is five times the other, then the value of k is
(a) 2
(b) 3
(c) 10
(d) 7
Question.4. Which of the following could be the equation of the given graph?
(a) (x+1)^{2} = (x-3)^{2}+5
(b) x+9 = 3-2x
(c) 1+x^{3} = 2
(d) 2x^{2}+3x-6=0
Question.5. The zeros of the polynomial 6x^{2}-3-7x are
(a) 6, –7
(b) 3, –7
(c) \frac{3}{2} , \frac{-1}{3}
(d) \frac{3}{2} , \frac{1}{3}
Ans.1. (b)
Ans.2. (d)
Ans.3. (d)
Ans.4. (d)
Ans.5. (c)
Case Study Question 30
Read the following and answer any four questions from 1 to 5.
A few children are playing with a skipping rope. When two of them hold it in their hands, as shown in the figure, it formed a mathematical shape.
Question.1. The name of the shape formed is
(a) parabola
(b) ellipse
(c) oval
(d) spiral
Question.2. If the graph of a polynomial has such a shape, it is always
(a) linear
(b) quadratic
(c) cubic
(d) None of these
Question.3. If the polynomial x^{2}+kx-15 represents such a curve, with one of its zeros as 3, then the value of k is
(a) 3
(b) 5
(c) 2
(d) –2
Question.4. If both the zeros of a quadratic polynomial ax^{2}+bx+c are equal and opposite in sign, then value of b is
(a) 1
(b) –1
(c) 2
(d) 0
Question.5. If the graph of a polynomial intersects the x-axis at only one point, then it
(a) is always a linear polynomial
(b) can be a quadratic polynomial
(c) can never be a quadratic polynomial
(d) can neither be linear nor quadratic polynomial
Ans.1. (a)
Ans.2. (b)
Ans.3. (c)
Ans.4. (d)
Ans.5. (b)