Hint: Give example(s) in order to define perimeter of closed figures.
Question.1. Jatin is finding the perimeter of a figure. Which of these could be the figure?
(a) 
Question.2. In which of these situations will perimeter be calculated?
(a) Length of lace border needed to put around a rectangular table cover.
(b) Length of rope required to fence three sides of a rectangular backyard.
(c) Amount of water needed to fill a container.
(d) Amount of paint required to paint a wall.
Ans.1. (d) 
Hint: Deduce and apply the formula to determine the perimeter of a rectangle.
Question.3. Aditi wants to put decorative tape around the borders of a rectangular cardboard which is 50 cm long and 45 cm wide. Which of these expressions represents the length of tape, in cm, required to cover its borders?
(a) (50 × 45)
(b) (50 + 45)
(c) 2(50 × 45)
(d) 2(50 + 45)
Question.4. A student has to form distinct rectangles by using coloured ribbon and paste it on a sheet. If she uses 20 centimetres of ribbon for each rectangle, how many distinct rectangles she can form of dimensions of positive integers?
(a) 1
(b) 5
(c) 6
(d) 10
Ans.3. (d) 2(50 + 45)
Ans.4. (b) 5
Hint: Deduce and apply the formula to determine the perimeter of a square.
Question.5. Arjun wants to fence his square backyard of side length 11 m using rope. He makes 3 complete rounds using the rope to fence. What is the total length of rope used?
(a) 44 m
(b) 66 m
(c) 132 m
(d) 363 m
Question.6. The perimeter of a square is 2k cm. If the perimeter of square becomes \frac{1}{2}k cm, how will the side length of the square change?
(a) It will become 4 times
(b) It will become 8 times
(c) It will become one-fourth
(d) It will become one-eighth
Ans.5. (c) 132 m
Ans.6. (c) It will become one-fourth
Hint: Deduce and generalize the formula to determine the perimeter of a regular polygon.
Question.7. A wire of length 56 cm is made into the shape of a heptagon. What is the side length of the heptagon?
(a) 7 cm
(b) 8 cm
(c) 14 cm
(d) 49 cm
Question.8. The perimeter of a regular hexagon is 14 cm less than the perimeter of a regular octagon. If the side length of the hexagon is (2k+3) cm, what is the side length of the octagon?
(a) (2k+5) cm
(b) (2k-13) cm
(c) \frac{1}{2}(3k+1) cm
(d) \left(\frac{3}{2}k+4\right) cm
Ans.7. (b) 8 cm
Ans.8. (d) \left(\frac{3}{2}k+4\right) cm
Hint: Give examples in order to defend that different shapes can have the same perimeter.
Question.9. Consider two shapes shown.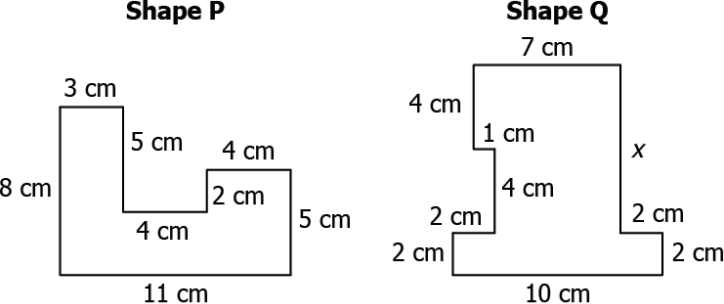
(a) 5
(b) 8
(c) 10
(d) 16
Question.10. Consider a figure below.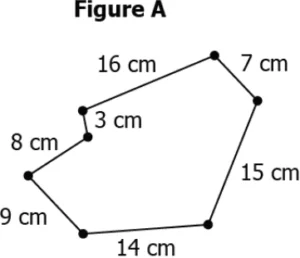
(a) A rectangle of length 12 cm and breadth 6 cm.
(b) An equilateral triangle of side length 24 cm.
(c) A regular pentagon of side length 9 cm.
(d) A square of side length 36 cm.
Ans.9. (a) 5
Ans.10. (b) An equilateral triangle of side length 24 cm.
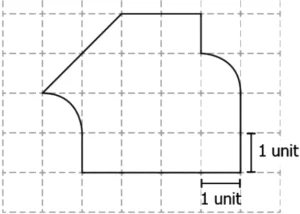
Hint: Count the squares in order to estimate the area of the given closed curve in the squares grid sheet.
Question.11. What is the area of the following figure?
(a) 13 square units
(b) 15 square units
(c) 16 square units
(d) 17 square units
Question.12. A farmer needs to buy seeds for a piece of agricultural land represented on a rectangular grid as shown below.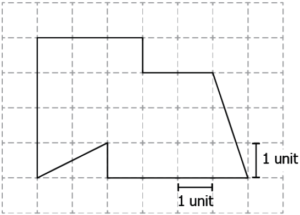
(a) 18.5
(b) 22.5
(c) 74
(d) 78
Ans.11. (b) 15 square units
Ans.12. (c) 74
Hint: Deduce and apply the formula in order to determine the area of a rectangle.
Question.13. The length of a rectangle is twice its breadth. Given that the length of the rectangle is 8 cm, what is the area of the rectangle?
(a) 24 cm^{2}
(b) 32 cm^{2}
(c) 48 cm^{2}
(d) 128 cm^{2}
Question.14. The length and breadth of a rectangle are changed such that the area of the rectangle changes from 2k to k. If the length and breadth of the original rectangle are l and b respectively, which of these could be the length and breadth of the new rectangle?
(a) \frac{l}{4} and 2b
(b) \frac{l}{2} and \frac{b}{2}
(c) \frac{l}{2} and 4b
(d) \frac{l}{4} and 4b
Ans.13. (b) 32 cm^{2}
Ans.14. (a) \frac{l}{4} and 2b
Hint: Deduce and apply the formula in order to determine the area of a square.
Question.15. Observe the figure below: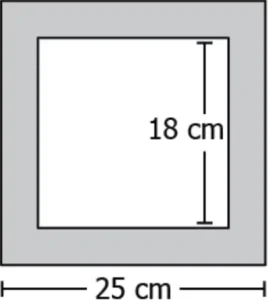
(a) 14 cm^{2}
(b) 28 cm^{2}
(c) 301 cm^{2}
(d) 949 cm^{2}
Question.16. If the side length of a square becomes one-third of the original side length, what is the ratio of the area of the original square to the area of square with changed side length?
(a) 1:3
(b) 1:9
(c) 3:1
(d) 9:1
Ans.15. (c) 301 cm^{2}
Ans.16. (d) 9:1