Hint: Recall natural numbers, whole numbers, integers and Rational numbers in order to classify a given number as either of them.
Question.1. Which statement is NOT true?
(a) 11 is an integer
(b) -5 is a whole number
(c) 8 is a natural number
(d) 3 is a rational number
Question.2. A number is of the form \frac{-q}{2}. Given that it is a whole number, an integer and a rational number, which of these is true?
(a) q<0 and the digit in the unit place of q is 2, 4, 6, 8, 0.
(b) q>0 and the digit in the unit place of q is 2, 4, 6, 8, 0.
(c) q<0 and the digit in the unit place of q is 1, 3, 5, 7, 9.
(d) q>0 and the digit in the unit place of q is 1, 3, 5, 7, 9.
Ans.1. (b) -5 is a whole number
Ans.2. (a) q<0 and the digit in the unit place of q is 2, 4, 6, 8, 0.
Hint: Represent a given number in the form \frac{p}{q} in order to show whether the given number is rational or not.
Question.3. A student represents an integer 8 as 81. Which of the following is true about the integer?
(a) It is a rational number as it is in the form \frac{p}{q}, where q≠0.
(b) It is an irrational number as it is in the form \frac{p}{q}, where q≠0.
(c) It is not a rational number as rational number is in the form \frac{p}{q}, where q≠1.
(d) It is not an irrational number as irrational number is in the form \frac{p}{q}, where q≠1.
Question.4. Is -10 a rational number? Why or why not?
(a) No, as -10=\frac{-10}{0} and rational numbers are ratio of integers m and n, where n≠0.
(b) Yes, as -10=\frac{-10}{1} and rational numbers are ratio of integers m and n, where n≠0.
(c) No, as -10=\frac{-10}{1} and rational numbers are ratio of integers m and n, where n≠1.
(d) Yes, as -10=\frac{-10}{0} and rational numbers are ratio of integers m and m.
Ans.3. (a) It is a rational number as it is in the form \frac{p}{q}, where q≠0.
Ans.4. (b) Yes, as -10=\frac{-10}{1} and rational numbers are ratio of integers m and n, where n≠0.
Hint: Calculate and find rational numbers between any 2 rational numbers in order to prove that there are infinite rational numbers between any 2 given rational numbers.
Question.5. Which rational number lies between \frac{1}{3} and \frac{3}{4}?
(a) 2\left(\frac{1}{3}+\frac{3}{4}\right)
(b) 2\left(\frac{1}{3}-\frac{3}{4}\right)
(c) \frac{1}{2}\left(\frac{1}{3}+\frac{3}{4}\right)
(d) \frac{1}{2}\left(\frac{1}{3}-\frac{3}{4}\right)
Question.6. Some of the rational numbers between 7 and 11 can be expressed in the form \frac{m}{6}, where m belongs to a set of natural numbers. Which of the following statement is true?
(a) All possible values of m lie between 42 and 66.
(b) All possible values of m lie between 42 and 77
(c) All possible values of m lie between 48 and 60.
(d) All possible values of m lie between 66 and 77.
Ans.5. (c) \frac{1}{2}\left(\frac{1}{3}+\frac{3}{4}\right)
Ans.6. (a) All possible values of m lie between 42 and 66.
Hint: Modify a given non-terminating decimal number in the form of \frac{p}{q} in order to comment whether this number is irrational.
Question.7. Which of the following is true about x=0.\overline{6}?
(a) x is a rational number because x can be written in the form \frac{p}{q} by solving the equation 10x=6+x.
(b) x is a rational number because x can be written in the form \frac{p}{q} by solving the equation 10x=6-x.
(c) x is an irrational number because x can be written in the form \frac{p}{q} by solving the equation 10x=6+x.
(d) x is an irrational number because x can be written in the form \frac{p}{q} by solving the equation 10x=6-x.
Question.8. Which of these is equivalent to 0.5\overline{782}?
(a) \frac{5772}{9990}
(b) \frac{5777}{9990}
(c) \frac{5782}{9990}
(d) \frac{5787}{9990}
Ans.7. (a) x is a rational number because x can be written in the form \frac{p}{q} by solving the equation 10x=6+x.
Ans.8. (b) \frac{5777}{9990}
Hint: Use Pythagoras’ theorem and create a Pythagorean triplet in order to construct the length of root of a given number.
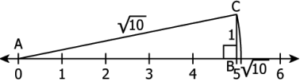
Question.9. Which of the following represents \sqrt{10} on a number line?
(a) 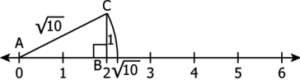
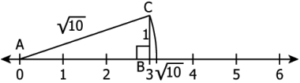
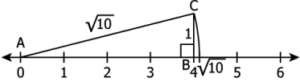
Question.10. Kevin’s work to represent 27 on a number line is shown.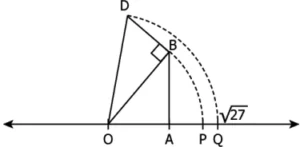
Looking at Kevin’s work, Tina and Ajay made following statements.
Tina: OA = 5 units, AB = BD = 1 unit
Ajay: OB = 26 units and AB = 1 unit
Who is correct?
(a) Only Tina
(b) Only Ajay
(c) Both of them
(d) Neither of them
Ans.9. (b) 
Hint: Deduce the value of a given fraction in its decimal form in order to infer if the decimal number is terminating or non-terminating.
Question.11. Which of the following rational numbers is equivalent to a decimal that terminates?
(a) \frac{1}{3}
(b) \frac{3}{8}
(c) \frac{5}{6}
(d) \frac{8}{9}
Question.12. A rational number m is described below.
m=\frac{Prime number}{15}
Consider the following conclusions about the number m.
Conclusion 1: The decimal expansion of m is non-terminating recurring but the decimal expansion of 3m is terminating.
Conclusion 2: The decimal expansion of m is terminating.
Which of these is correct?
(a) Conclusion 1 is valid but Conclusion 2 is valid only for the prime number 3.
(b) Conclusion 1 is valid but Conclusion 2 is valid only for the prime number 5.
(c) Conclusion 1 is not valid but Conclusion 2 is valid only for the prime number 3.
(d) Conclusion 1 is not valid but Conclusion 2 is valid only for the prime number 5.
Ans.11. (b) \frac{3}{8}
Ans.12. (a) Conclusion 1 is valid but Conclusion 2 is valid only for the prime number 3.
Hint: Compute the commutative, associative and distributive laws for addition and multiplication for irrational numbers in order to determine whether the sum, difference, quotients and products of irrational numbers are irrational or not.
Question.13. Which of the following is an irrational number?
(a) \frac{\sqrt{12}}{\sqrt{3}}
(b) \frac{\sqrt{18}}{\sqrt{2}}
(c) \frac{\sqrt{45}}{\sqrt{5}}
(d) \frac{\sqrt{42}}{\sqrt{7}}
Question.14. An expression is given: 2(\sqrt{k}-1)+\sqrt{8}
If on adding -8\sqrt{2} to the expression results in a rational number, what is the value of k?
(a) 6
(b) 12
(c) 18
(d) 36
Ans.13. (d) \frac{\sqrt{42}}{\sqrt{7}}
Ans.14. (c) 18
Hint: Rationalize the denominator of a given expression with a square root term in the denominator in order to convert it to an equivalent expression whose denominator is a rational number.
Question.15. Which of these is a way to convert \frac{15}{\sqrt{63}+\sqrt{20}} to an equivalent number whose denominator is a rational number?
(a) \frac{15}{\sqrt{63}+\sqrt{20}}\times \frac{(3\sqrt{7}-2\sqrt{5})}{(3\sqrt{7-2\sqrt{5}})}
(b) \frac{15}{\sqrt{63}+\sqrt{20}}\times \frac{(3\sqrt{7}-4\sqrt{5})}{(3\sqrt{7-4\sqrt{5}})}
(c) \frac{15+(3\sqrt{7}-4\sqrt{5})}{(\sqrt{63}+\sqrt{20})\times(3\sqrt{7}-4\sqrt{5})}
(d) \frac{15+(3\sqrt{7}-2\sqrt{5})}{(\sqrt{63}+\sqrt{20})\times(3\sqrt{7}-2\sqrt{5})}
Question.16. On a number line, \frac{2}{\sqrt{8}} is halfway located between 0 and \sqrt{a}. What is the value of a?
(a) 1
(b) 2
(c) 4
(d) 8
Ans.15. (a) \frac{15}{\sqrt{63}+\sqrt{20}}\times \frac{(3\sqrt{7}-2\sqrt{5})}{(3\sqrt{7-2\sqrt{5}})}
Ans.16. (b) 2
Hint: Extend the law of exponents in order to simplify a given expression.
Question.17. Which of these is equivalent to 9^{\frac{3}{4}}\times 27^{\frac{1}{5}}?
(a) 3^{{\frac{3}{4}}+{\frac{3}{5}}}
(b) 3^{{\frac{3}{2}}+{\frac{3}{5}}}
(c) 3^{{\frac{3}{4}}-{\frac{3}{5}}}
(d) 3^{{\frac{3}{2}}-{\frac{3}{5}}}
Question.18. If ({p^{\frac{1}{3}}\times 5^{\frac{1}{4}}})^{\frac{1}{2}}\times {\left(\frac{3^{\frac{1}{4}}}{q^{\frac{1}{5}}}\right)}^{2}=\frac{3^{\frac{5}{6}}}{5^{\frac{3}{40}}}, then what are the values of p and q?
(a) p=3 and q=5
(b) p=9 and q=5
(c) p=3 and q=25
(d) p=9 and q=25
Ans.17. (b) 3^{{\frac{3}{2}}+{\frac{3}{5}}}
Ans.18. (d) p=9 and q=25