Hint: Define segment, ray, collinear points, non-collinear points, acute angle, right angle, obtuse angle, straight angle, reflex angle, complementary angles, Supplementary angles in order to identify them in a given figure.
Question.1. Tina drew a figure and named it \overleftrightarrow{JK}. Which of the following best describes the figure Tina drew?
(a) It is an angle.
(b) It is a line segment.
(c) It could be a line segment or a ray.
(d) It could be a line or a line segment.
Question.2. Two angles are supplementary. One of them is an acute angle. Which of these could be the measure of the other angle?
(a) 60°
(b) 90°
(c) 120°
(d) 180°
Ans.1. (c) It could be a line segment or a ray.
Ans.2. (c) 120°
Hint: Label angles created by two intersecting lines in order to identify vertically opposite pairs, adjacent angles, linear pairs, complementary/supplementary pairs of angles.
Question.3. Two intersecting lines are shown.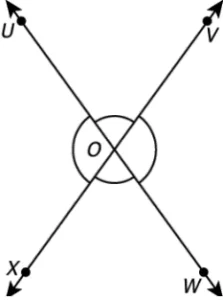
(a) \angleXOW and \angleUOV is a pair of vertically opposite angles.
(b) \angleUOV and \angleVOW are supplementary angles.
(c) \angleUOX and \angleXOW are linear pair of angles.
(d) \angleUOX and \angleVOW are adjacent angles.
Question.4. Which words complete the statement below?
When two lines intersect, _____ pairs of adjacent angles are formed and all pairs are ______.
(a) 2; supplementary
(b) 4; supplementary
(c) 2; complementary
(d) 4; complementary
Ans.3. (d) \angleUOX and \angleVOW are adjacent angles.
Ans.4. (b) 4; supplementary
Hint: Apply the concepts of linear pairs of angles and vertically opposite angles in order to establish relationships between the angles in a given figure and solve for missing values.
Question.5. Two intersecting lines are shown.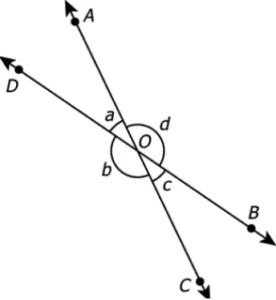
(a) a=30°, b=150°, c=30°
(b) a=150°, b=150°, c=30°
(c) a=30°, b=30°, c=150°
(d) a=30°, b=150°, c=150°
Question.6. Harish places two straws forming angles a and b as shown.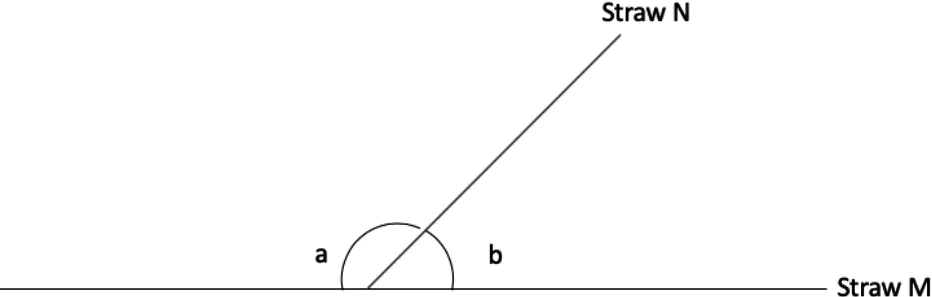
(a) The value of a triples.
(b) The value of a reduces by 2b.
(c) The value of a increases by 2b.
(d) The value of a becomes \frac{1}{3} times.
Ans.5. (a) a=30°, b=150°, c=30°
Ans.6. (b) The value of a reduces by 2b.
Hint: Label angles created by a transversal intersecting two parallel lines in order to identify corresponding angles, alternate angles, interior angles and define relationship between these angles.
Question.7. In the figure below, m and n are two parallel lines and p is a transversal.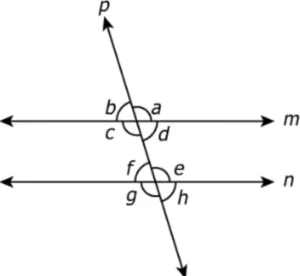
(a) c+e=180° as c and e are alternate interior angles.
(b) d=h as d and h are corresponding angles.
(c) b=g as b and g are corresponding angles.
(d) a=e as a and e are alternate interior angles.
Question.8. In the figure below, l and m are two parallel lines intersecting by a transversal n.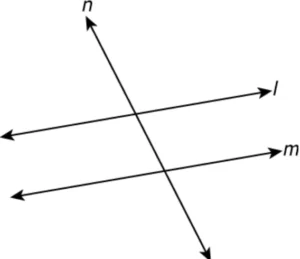
(a) 2
(b) 8
(c) 4
(d) 6
Ans.7. (b) d=h as d and h are corresponding angles.
Ans.8. (c) 4
Hint: Solve for the value of unknown angles created by a transversal in a given figure in order to infer If the lines are parallel or not.
Question.9. Two lines are cut by a transversal as shown.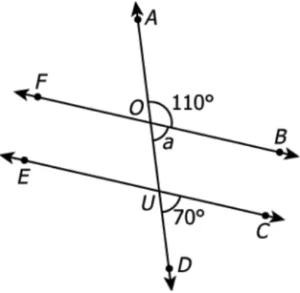
(a) Yes, because a= \angle CUD = 70° and congruent alternate interior angles indicates that BF and CE are parallel.
(b) Yes, because a= \angle CUD = 70° and congruent corresponding angles indicates that BF and CE are parallel.
(c) No, because a≠ \angle CUD indicating that corresponding angles are not congruent
(d) No, because \angle AOB and \angle CUD are alternate interior angles but not equal in measure.
Question.10. Two lines are cut by a transversal as shown.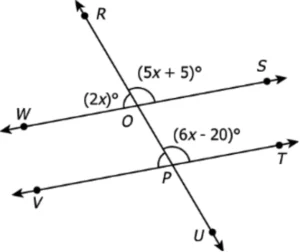
(a) Yes, because corresponding angles, \angle TPO and \angle SOR are equal in measure and their measure is 130°.
(b) No, because \angle TPO = 155°and \angle SOR = 160°; this indicate that corresponding angles are not equal.
(c) No, because \angle TPO = 130° and \angle SOR = 150°; this indicate that corresponding angles are not equal.
(d) Yes, because alternate angles, \angle TPO and \angle SOR are equal in measure and their measure is 130°.
Ans.9. (b) Yes, because a= \angle CUD = 70° and congruent corresponding angles indicates that BF and CE are parallel.
Ans.10. (a) Yes, because corresponding angles, \angle TPO and \angle SOR are equal in measure and their measure is 130°.
Hint: Define relationship between angles formed when a triangle is placed between two parallel lines in order to prove that exterior angle of a triangle is the sum of the two opposite interior angles.
Question.11. Consider a triangle that lies between the parallel lines.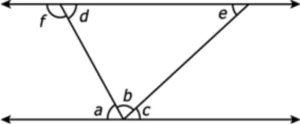
(a) Yes; As \angle f = \angle b + \angle c and \angle c = \angle e
(b) Yes; As \angle f = \angle b and \angle c = \angle e
(c) The given statement is not true.
(d) Yes; As \angle f = \angle b and \angle e = \angle b +\angle c
Question.12. In the figure below, ∆ABC lies between the parallel lines.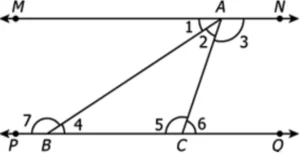
(a) Corresponding angles are congruent
(b) Alternate interior angles are congruent
(c) Linear pair postulate
(d) Angle sum property of triangle
Ans.11. (a) Yes; As \angle f = \angle b + \angle c and \angle c = \angle e
Ans.12. (b) Alternate interior angles are congruent




