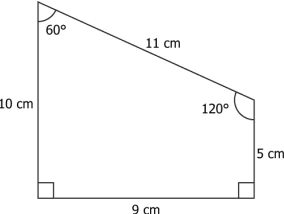
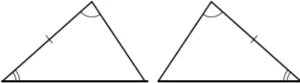
Hint: Observe the angles and sides of the given figures in order to show that they are congruent or not congruent.
Question.1. A figure is shown.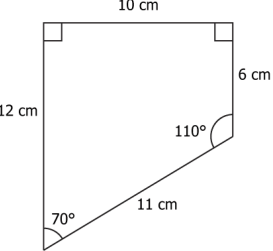
(a) 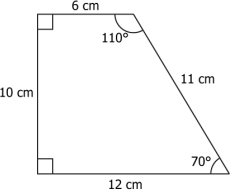
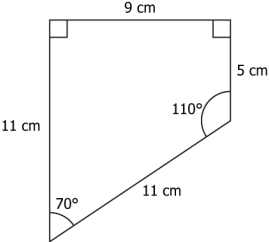
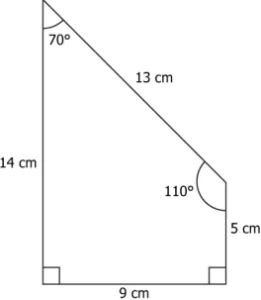
Question.2. Consider the following two statements about the rectangles a student draws.
Statement 1: Rectangles have the same perimeter.
Statement 2: Rectangles have the same area.
Which of the following statements is sufficient to conclude that the rectangles are congruent?
(a) Statement 1 alone is sufficient, but statement 2 alone is not sufficient.
(b) Statement 2 alone is sufficient, but statement 1 alone is not sufficient.
(c) Both statements together are sufficient, but neither statement alone is sufficient.
(d) Both statements together are not sufficient.
Ans.1. (a) 
Hint: Apply concepts of linear pairs of angles, vertically opposite angles, corresponding angles, alternate angles, transversal angles & exterior angles of a triangle in order to prove congruence between 2 triangles in a given figure.
Question.3. Consider the triangles made by two intersecting lines as shown.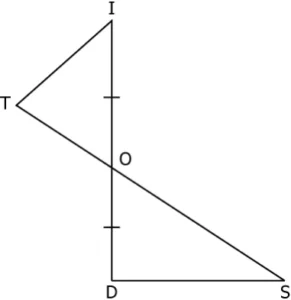
(a) \angleDOS = \angleTOI
(b) \angleOTI = \angleODI
(c) TO = OS
(d) TI = DS
Question.4. Consider the parallelogram as shown.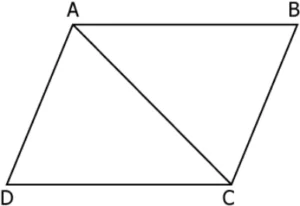
(a) Yes, because AB = CD, AD = BC, \angleDAC = \angleACB, \angleDCA = \angleCAB, \angleADC = \angleABC and AC = AC.
(b) Yes, because AB = CD, AD = BC, \angleDAC = \angleCAB, \angleDCA = \angleACB, \angleADC = \angleABC and AC = AC.
(c) No, because angle measures are not known.
(d) No, because side lengths are not known.
Ans.3. (c) TO = OS
Ans.4. (a) Yes, because AB = CD, AD = BC, \angleDAC = \angleACB, \angleDCA = \angleCAB, \angleADC = \angleABC and AC = AC.
Hint: Illustrate the criterions of congruencies of triangles through diagrams (ASA, SAS, SSS. RHS) in order to prove relationships between given angles, sides and triangles of a given figure.
Question.5. Consider the triangles shown.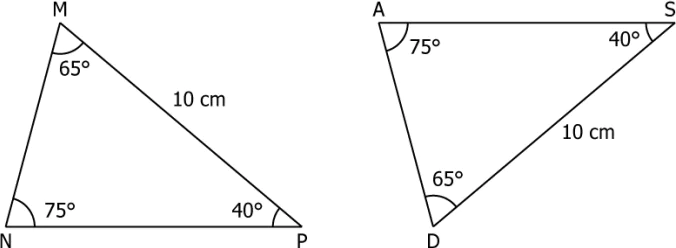
(a) SSS
(b) SAS
(c) AAA
(d) ASA
Question.6. Consider the triangles shown.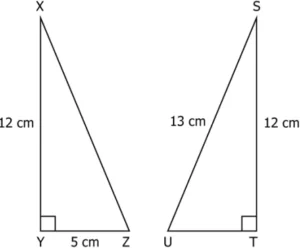
(a) ∆XYZ ≅ ∆STU (by SSS congruence rule).
(b) ∆XYZ ≅ ∆STU (by RHS congruence rule).
(c) ∆XYZ ≅ ∆STU (by ASA congruence rule).
(d) ∆XYZ ≅ ∆STU (by SAS congruence rule).
Ans.5. (d) ASA
Ans.6. (c) ∆XYZ ≅ ∆STU (by ASA congruence rule).
Hint: Apply criterions for congruence in a triangle with two congruent sides in order to prove that the angle opposite to the sides are equal and apply it in a given figure to solve for the measure of an angle.
Question.7. In triangle ZAT, AZ = AT and AE bisects \angleZAT.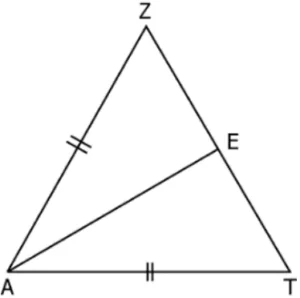
(a) \angleZAE
(b) \angleZTA
(c) \angleAET
(d) \angleAEZ
Question.8. In the triangle below, AD is the bisector of \angleA and AB = AC.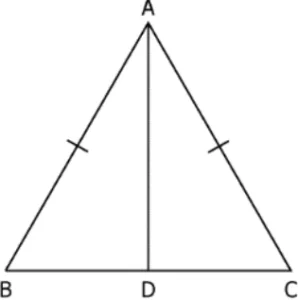
By _____ congruency criteria, ∆ABD ≅ ∆ACD and using CPCTC, we get \angleABC = ____.
(a) ASA; \angleACD
(b) SAS; \angleACD
(c) ASA; \angleADC
(d) SAS; \angleADC
Ans.7. (a) \angleZAE
Ans.8. (b) SAS; \angleACD
Hint: Examine given triangles that satisfy AAA or SSA criteria in order to comment whether they are congruent.
Question.9. Which of these pairs of triangles are not congruent?
(a) 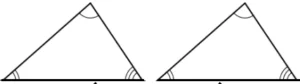
Question.10. Two triangles are shown. 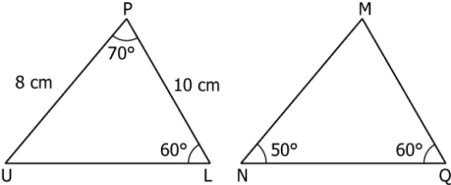
(a) Yes, as on calculating the missing angle in each triangle it can be concluded that the triangles are congruent by AAA criteria.
(b) No, as the missing angle in each triangle cannot be calculated.
(c) Conclusion about the congruency of triangles can be made provided the length of the side NQ of triangle MNQ is known.
(d) Conclusion about the congruency of triangles can be made provided the length of the side MN or side MQ of triangle MNQ is known.
Ans.9. (a) 
Hint: Using properties of triangles prove the relationship between any given sides or angles in a given figure.
Question.11. In the given triangle, LN = MN.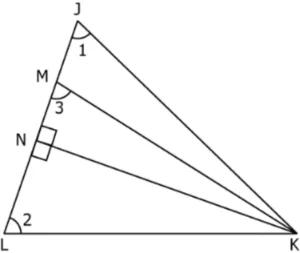
(a) 9 cm
(b) 13 cm
(c) 17 cm
(d) 26 cm
Ans.11. (a) 9 cm