Competency Based Questions for Class 10 Maths Chapter 6 Triangles

Competency Based Questions are new type of questions asked in CBSE Board exam for class 10. Practising the following Competency Based Questions will help the students in facing Board Questions.

Hint: Distinguish between congruency and similarity in order to understand the concept of similar figures.

Question.1. Rahul claims that congruent figures are similar as well. Aman claims that similar figures are congruent as well. Who is/are correct?

(a) only Rahul
(b) only Aman
(c) Both Rahul and Aman
(d) Neither Rahul nor Aman

Answer. (a) only Rahul

Question.2. Consider the statements below.
Statement 1: All circles are similar.
Statement 2: All squares are similar.
Statement 3: All right triangles are congruent.
Statement 4: All equilateral triangles are congruent.
Which statement is/are correct?

(a) Statement 1 and Statement 3
(b) Statement 2 and Statement 4
(c) Statement 1 and Statement 2
(d) Statement 3 and Statement 4

Answer. (c) Statement 1 and Statement 2

Hint: Distinguish between congruency and similarity in order to understand the concept of similar figures.

Question.3. Two similar figures are shown. 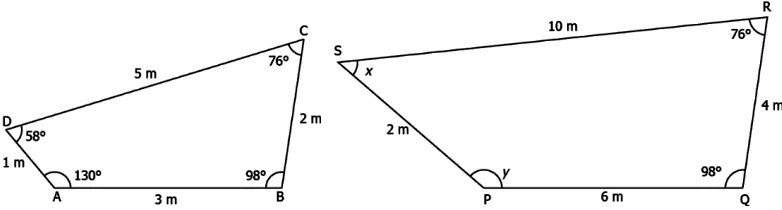What are the values of x and y?

(a) x=58°, y=130°
(b) x=98°, y=76°
(c) x=82°, y=84°
(d) x=130°, y=84°

Answer. (a) x=58°, y=130°

Question.4. Two quadrilaterals are such that their diagonals bisect each other. What additional information is required to conclude that the quadrilaterals are similar?

(a) Opposite sides are equal
(b) Opposite angles are equal
(c) Diagonals are equal and opposite sides are equal
(d) Diagonals bisect at right angle and adjacent angles are equal

Answer. (d) Diagonals bisect at right angle and adjacent angles are equal

Hint: Compute the angles and ratio of sides of triangles in order to determine their similarity.

Question.5. Consider the figure below. 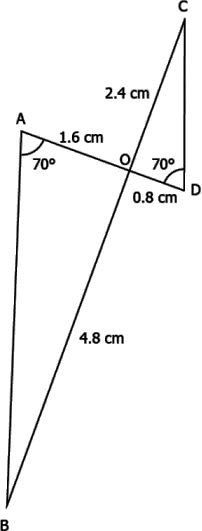Which of the following statement is correct about the triangles in the figure?

(a) ∆AOB~∆DOC because \frac{AO}{DO}=\frac{BO}{CO}.
(b) ∆AOB~∆DOC because \angle AOB=\angle DOC.
(c) ∆AOB~∆DOC because \frac{AO}{DO}=\frac{BO}{CO} and \angle AOB=\angle DOC.
(d) ∆AOB~∆DOC because \frac{AO}{DO}=\frac{BO}{CO} and \angle BAO=\angle CDO.

Answer. (c) ∆AOB~∆DOC because \frac{AO}{DO}=\frac{BO}{CO} and \angle AOB=\angle DOC.

Question.6. Consider the figure below. 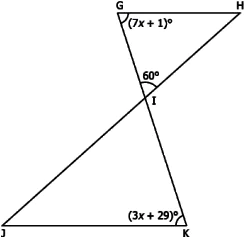Which of the following information help proving that triangle GHI is similar to triangle KIJ?
Information 1: \angle H=70°
Information 2: \angle J=70°

(a) Each information alone is sufficient
(b) Information (1) alone is sufficient, but Information (2) alone is not sufficient.
(c) Information (2) alone is sufficient, but Information (1) alone is not sufficient.
(d) Both information together is sufficient, but neither information alone is sufficient.

Answer. (a) Each information alone is sufficient

Hint: Apply basic proportionality theorem and its converse in order to determine the ratio of sides in the given triangle(s).

Question.7. In the figure below, BA \parallel QR. 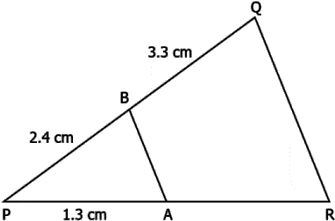To the nearest tenth, what is the length of AR?

(a) 1.8 cm
(b) 1.7 cm
(c) 1.4 cm
(d) 2.2 cm

Answer. (a) 1.8 cm

Question.8. In the given figure, QR \parallel AB, RP \parallel BD, CQ=x+2, QA=x, CP=5x+4, PD=3x. 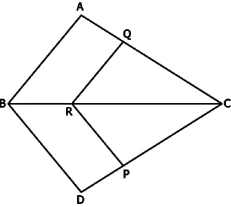The value of x is __.

(a) 1
(b) 3
(c) 6
(d) 9

Answer. (a) 1

Hint: Apply various criterions of similarity in order to prove that whether given triangles are similar or not.

Question.9. Observe the two triangles shown below. 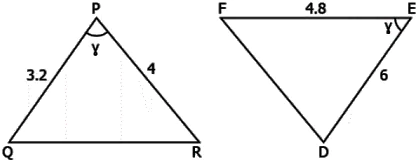Which statement is correct?

(a) Triangles are similar by SAS
(b) Triangles are similar by SSA
(c) Triangles are not similar as sides are not in proportion
(d) No valid conclusion about similarity of triangles can be made as angle measures are not known.

Answer. (a) Triangles are similar by SAS

Question.10. Consider the triangles below. 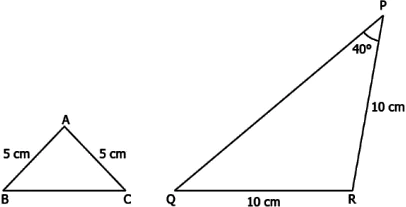Which statement is correct?

(a) Triangles are similar as all isosceles triangles are similar.
(b) Triangles are similar as corresponding sides of the triangles are in the ratio 1:2.
(c) For triangles to be similar, the measure of \angle A=40°.
(d) For triangles to be similar, the measure of \angle A=100°.

Answer. (d) For triangles to be similar, the measure of angle A=100°.

Hint: Show similarity of triangles in order to solve for given real life word problems.

Question.11. Nishant is 6 feet tall. At an instant, his shadow is 5 feet long. At the same instant, the shadow of a pole is 30 feet long. How tall is the tower?

(a) 24 feet
(b) 30 feet
(c) 36 feet
(d) 18 feet

Answer. (c) 36 feet

Question.12. Rahul is 5 feet tall. He places a mirror on the ground and moves until he can see the top of a building. At the instant when Rahul is 2 feet from the mirror, the building is 48 feet from the mirror. How tall is the building?

(a) 120 feet
(b) 96 feet
(c) 240 feet
(d) 180 feet

Answer. (a) 120 feet

Hint: Compute the square of the ratio of the corresponding sides of triangles in order to find the area of similar triangles.

Question.13. The area of two similar triangles are a and k^{2}a. What is the ratio of the corresponding side lengths of the triangles?

(a) 1:k^{2}
(b) 1:k
(c) 1:a^{2}
(d) 1:a

Answer. (b) 1:k

Question.14. In the figure below, XY \parallel BC. 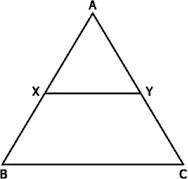The ratio of the perimeter of triangle ABC to the perimeter of triangle AXY is 3:1. Given that the numerical value of the area of triangle AXY is a whole number, which of the following could be the area of the triangle ABC?

(a) 28
(b) 55
(c) 60
(d) 99

Answer. (d) 99

Hint: Compute the area of similar triangles in order to find the relation between their sides, medians, mid points of the triangles.

Question.15. The ratio of the areas of two similar triangles, ABC and PQR shown below is 25:144.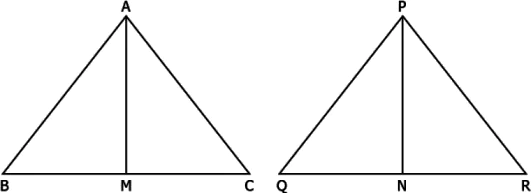 What is the ratio of their medians AM and PN?

(a) 5:12
(b) 25:144
(c) 12:5
(d) 5:16

Answer. (a) 5:12

Question.16. The ratio of the areas of two similar right triangles is 9:16. The length of one of the sides of the smaller triangle is 15 cm. How much longer is the length of the corresponding side of the larger triangle from smaller triangle?

(a) 3 cm
(b) 4 cm
(c) 5 cm
(d) 7 cm

Answer. (c) 5 cm

Hint: Apply the theorem that if a perpendicular is drawn from the vertex of the right angle of a right triangle to the hypotenuse then triangles on both sides of the perpendicular are similar to the whole triangle in order to prove Pythagoras Theorem and to each other.

Question.17. Observe the right triangle ABC, right angled at B as shown below.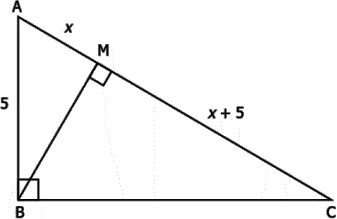 What is the length of MC?

(a) 7.5 cm
(b) 2.5 cm
(c) 6.5 cm
(d) 10.5 cm

Answer. (a) 7.5 cm

Question.18. Observe the right triangle PQR, right angled at Q as shown below.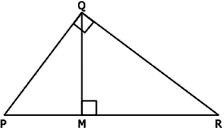 If QM \perp PR, then which of the following is NOT correct?

(a) \triangle PMQ \sim \triangle PQR
(b) QR^{2}=RM \cdot PR
(c) PR^{2}=PQ \cdot RQ
(d) \triangle PMQ \sim \triangle QMR

Answer. (c) PR^{2}=PQ cdot RQ

Hint: Prove Pythagoras theorem and its converse in order to solve real life word problems and mathematical statements/questions.

Question.19. Consider the figure below. 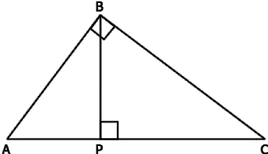Rahul follows the below step to prove AB^{2}+BC^{2}=AC^{2}.
Step 1: \triangle APB\\sim \triangle ABC
Step 2: \frac{AP}{AB}=\frac{AB}{AC}
Step 3: AB^{2}=AP \cdot AC
Which of these could be his next step?

(a) Prove \triangle ABC \sim \triangle PAB
(b) Prove \triangle APB \sim \triangle CPB
(c) Prove \triangle BPC \sim \triangle ABC
(d) Prove \triangle APB \sim \triangle BPC

Answer. (c) Prove triangle BPC sim triangle ABC

Question.20. From point X, Ankit walks 112 m east to reach at point Y. From point Y, Ankit walks 15 m toward north to reach point Z. What is the straight-line distance between position when he started and his position now?

(a) 123 m
(b) 127 m
(c) 117 m
(d) 113 m

Answer. (d) 113 m

Hint: Apply Pythagoras theorem and its converse in order to determine whether a given triangle is a rightangled triangle or not.

Question.21. Which set of lengths forms a right triangle?

(a) 5 cm, 12 cm, 16 cm
(b) 7 cm, 24 cm, 25 cm
(c) 3 cm, 3 cm, 4 cm
(d) 6 cm, 7 cm, 9 cm

Answer. (b) 7 cm, 24 cm, 25 cm

Question.22. Consider the following three claims about a triangle JKL with side lengths m, n and r.
Claim 1: JKL is a right triangle provided n^{2}-m^{2}=r^{2}.
Claim 2: Triangle with side lengths m+2, n+2 and r+2 is a right-angle triangle.
Claim 3: Triangle with side lengths 2m, 2n and 2r is a right-angle triangle.
Which of these is correct?

(a) Claim 1 would be correct if n>m, n>r and Claim 2 would be correct if JKL is a right triangle.
(b) Claim 1 would be correct if r>m, r>n and Claim 2 would be correct if JKL is a right triangle.
(c) Claim 1 would be correct if n>m, n>r and Claim 3 would be correct if JKL is a right triangle.
(d) Claim 1 would be correct if r>m, r>n and Claim 3 would be correct if JKL is a right triangle.

Answer. (c) Claim 1 would be correct if n>m, n>r and Claim 3 would be correct if JKL is a right triangle.