Multiple Choice Questions (MCQs) Maths Class 10 Chapter 1 Real Numbers
Multiple Choice Questions
Question.1. Which of the following statement(s) is/are not correct?
(a) Every integer is a rational number.
(b) The sum of a rational number and an irrational number is an irrational number.
(c) Every real number is rational.
(d) Every point on a number line is associated with a real number.
Question.2. Two positive numbers have their HCF as 12 and their product as 6336. The number of pairs possible for the numbers, is
(a) 2
(b) 3
(c) 4
(d) 5
Ans.1. (c) Every real number is rational.
Ans.2. (a) 2
Explanation: Let the numbers be 12x and 12y where x and y are co-primes.
Product of these numbers = 144xy
Hence, 144xy=6336
⇒ xy=44
Since, 44 can be written as the product of two factors in three ways. i.e. (1\times 44), (2\times 22), (4\times 11). As x and y are coprime, so (x,y), can be (1,44) or (4,11) but not (2,22).
Hence, two possible pairs exist.
Question.3. Which of the following statement(s) is/are not correct?
(a) There are infinitely many even primes.
(b) Let ‘a’ be a positive integer and p be a prime number such that a^{2} is divisible by p, then a is divisible by p.
(c) Every positive integer different from 1 can be expressed as a product of non-negative power of 2 and an odd number.
(d) If ‘p’ is a positive prime, then \sqrt{p} is an irrational number.
Question.4. If X=28+(1\times 2\times 3 \times 4\times …\times 16\times 28) and Y=17+(1\times 2\times 3 \times 4\times …\times 17), then which of the following is/are true?
1. X is a composite number
2. X is a prime number
3. X-Y is a prime number
4. X+Y is a composite number.
(a) Both (1) and (4)
(b) Both (2) and (3)
(c) Both (2) and (4)
(d) Both (1) and (2)
Ans.3. (a)
Ans.4. (a) Both (1) and (4)
Explanation: We have, X=28+(1\times 2\times 3 \times 4\times …\times 16\times 28)
⇒ X=28[1+(1\times 2\times 3\times … \times 16)]
Hence, X is a composite number.
Also, we have
Y=17+(1\times 2\times 3 \times 4\times …\times 17)
⇒ Y=17[1+(1\times 2\times 3\times … \times 16)]
Hence, Y is a composite number.
Now, X-Y=[1+(1\times 2\times 3\times … \times 16)](28-17)
⇒ X-Y=[1+(1\times 2\times 3\times … \times 16)](11)
Hence, X-Y is a composite number.
and, X+Y=[1+(1\times 2\times 3\times … \times 16)](28+17)
⇒ X+Y=[1+(1\times 2\times 3\times … \times 16)](45)
Hence, X+Y is a composite number.
Question.5. The value of (12)^{3^{x}}+(18)^{3^{x}}, x∈N, end with the digit.
(a) 2
(b) 8
(c) 0
(d) Cannot be determined
Question.6. If n is an even natural number, then the largest natural number by which n(n+1)(n+2) is divisible, is
(a) 6
(b) 8
(c) 12
(d) 24
Ans.5. (c) 0
Explanation: For all x∈N, (12)^{3^{x}} ends with either 8 or 2 and (18)^{3^{x}} ends with either 2 or 8.
If (12)^{3^{x}} ends with 8, then (18)^{3^{x}} ends with 2.
If (12)^{3^{x}} ends with 2, then (18)^{3^{x}} ends with 8.
Thus, (12)^{3^{x}}+(18)^{3^{x}} ends with 0 only.
Ans.6. (d) 24
Explanation: Since n is divisible by 2 therefore (n+2) is divisible by 4, and hence n(n+2) is divisible by 8.
Also, n, (n+1), (n+2) are three consecutive numbers.
So, one of them is divisible by 3.
Hence, n(n+1)(n+2) must be divisible by 24.
Question.7. If p_{1} and p_{1} are two odd prime numbers such that p_{1}>p_{2}, then p_1^2-p_2^2 is
(a) an even number
(b) an odd number
(c) an odd prime number
(d) a prime number
Question.8. The rational form of 0.2\overline{54} is in the form of \frac{p}{q} then (p+q) is
(a) 14
(b) 55
(c) 69
(d) 79
Ans.7. (a) an even number
Explanation: p_1^2-p_2^2 is an even number.
Let us take p_{1}=5
and p_{2}=3
Then, p_1^2-p_2^2=25-9=16
16 is an even number.
Ans.8. (c) 69
Explanation: Let, x=0.2\overline{54}, then
x = 0.2545454… …(1)
Multiplying Eq. (1) by 100, we get
100x = 25.4545… …(2)
Subtracting Eq. (1) from Eq. (2), we get
99x = 25.2
⇒ x=\frac{252}{990}=\frac{14}{55}
Comparing with \frac{p}{q}, we get
p=14
and q = 55
Hence, p+q = 14+55=69
Question.9. If a=2^{3}\times 3, b=2\times 3\times 5, c=3^{n}\times 5 and LCM (a, b, c) = 2^{3}\times 3^{2}\times 5, then n=
(a) 1
(b) 2
(c) 3
(d) 4
Question.10. There sets of Mathematics, Science and Biology books have to be stacked in such a way that all the books are stored subject wise and the height of each stack is the same. The number of Mathematics books is 240, the number of Science books is 960 and the number of Biology books is 1024. The number of stack of Mathematics, Science and Biology books, assuming that the books are of the same thickness are respectively.
(a) 15, 60, 64
(b) 60, 15, 64
(c) 64, 15, 60
(d) None of these
Ans.9. (b) 2
Explanation: Value of n = 2
Ans.10. (a) 15, 60, 64
Explanation: The prime factorisation of 240, 960 and 1024 is given below:
240=2\times 2\times 2\times 2\times 3\times 5 = 2^{4}\times 3\times 5,
960=2\times 2\times 2\times 2\times 2\times 2\times 3\times 5 = 2^{6}\times 3\times 5
and 1024=2\times 2\times 2\times 2\times 2\times 2\times 2\times 2\times 2\times 2 = 2^{10}
HCF of 240, 960 and 1024 = 2^{4}=16
Hence, there must be 16 books in each stack.
Now, number of stacks of Mathematics books =\frac{240}{16}=15
Number of stacks of Science books =\frac{960}{16}=60
and, number of stacks of Biology books =\frac{1024}{16}=64
Question.11. If a+bp^{\frac{1}{3}}+cp^{\frac{2}{3}}=0, where a, b, c, p are rational numbers and p is not perfect cube, then
(a) a≠b=c
(b) a=b≠c
(c) a≠b≠c
(d) a=b=c
Question.12. The rational number of the form \frac{p}{q}, q≠0, p and q are positive integers, which represents 0.1\overline{34} i.e., (0.1343434……….) is
(a) \frac{134}{999}
(b) \frac{134}{990}
(c) \frac{133}{999}
(d) \frac{133}{990}
Ans.11. (d) a=b=c
Explanation: We have, a+bp^{\frac{1}{3}}+cp^{\frac{2}{3}}=0 …(1)
On multiplying both sides by p^{\frac{1}{3}}, we get
ap^{\frac{1}{3}}+bp^{\frac{1}{3}}\times p^{\frac{1}{3}}+cp^{\frac{2}{3}}\times p^{\frac{1}{3}}=0
⇒ ap^{\frac{1}{3}}+bp^{\frac{2}{3}}+cp^{\frac{3}{3}}=0
⇒ ap^{\frac{1}{3}}+bp^{\frac{2}{3}}+cp=0 …(2)
On multiplying Eq. (1) by b and Eq. (2) by c, then
subtracting Eq. (2) from Eq. (1), we get
(ab+b^{2}p^{\frac{1}{3}}+bcp^{\frac{2}{3}})-(acp^{\frac{1}{3}}+bcp^{\frac{2}{3}}+c^{2}p)=0
⇒ (b^{2}-ac)p^{\frac{1}{3}}+ab-c^{2}p=0
[Here, p^{\frac{1}{3}} is an irrational number and ab-c^{2}p is a rational number]
Note that, sum of rational and irrational numbers cannot be zero.
So, (b^{2}-ac)p^{\frac{1}{3}}+ab-c^{2}p=0, only if
(b^{2}-ac)=0 and ab-c^{2}p=0
⇒ b^{2}=ac …(3)
and ab=c^{2}p
⇒ a^{2}b^{2}=c^{4}p^{2} …(4)
[squaring both sides]
From Eq. (4),
a^{2}(ac)=c^{4}p^{2} [since, b^{2}=ac]
a^{3}c-c^{4}p^{2}=0
⇒ c=0 or a^{3}-c^{3}p^{2}=0
⇒ c=0 or p^{2}c^{3}=a^{3}
On taking, p^{2}=\frac{a^{3}}{c^{3}}
We get, (p^{2})^{\frac{1}{3}}=\frac{a}{c} which is not possible as p^{\frac{2}{3}} is an irrational number and \frac{a}{c} is a rational number.
Hence, c=0
On putting c=0 in Eq. (3), we get
b=0
On putting b=0, c=0 in Eq. (1), we get
a=0
Hence, a=b=c
Ans.12. (d) \frac{133}{990}
Explanation: 0.1\overline{34}=\frac{134-1}{990}=\frac{133}{990}
Question.13. If x and y are odd positive integers, then x^{2}+y^{2} is
(a) even and divisible by 4
(b) even and not divisible by 4
(c) odd and divisible by 4
(d) odd and not divisible by 4
Question.14. The least number which is a perfect square and is divisible by each of 16, 20 and 24 is
(a) 240
(b) 1600
(c) 2400
(d) 3600
Ans.13. (b) even and not divisible by 4
Explanation: We know that, any odd positive integer is of the form 2q+1, where q is any integer. So, x=2m+1 and y=2n+1 for some integers m and n.
Now, x^{2}+y^{2}=(2m+1)^{2}+(2n+1)^{2}
= 4m^{2}+1^{2}+4m+4n^{2}+1^{2}+4n
= 4(m^{2}+n^{2})+4(m+n)+2
= 4[(m^{2}+n^{2})+(m+n)]+2
= 4r+2
Where, r=m^{2}+n^{2})+m+n
Clearly, 4r+2 is an even number and not divisible by 4.
Hence, x^{2}+y^{2} is even but not divisible by 4.
Ans.14. (d) 3600
Explanation: The L.C.M. of 16, 20 and 24 is 240. The least multiple of 240 that is a perfect square is 3600 and also we can easily eliminate choices (a) and (c) since they are not perfect number.
Question.15. Which of the following rational number have non-terminating repeating decimal expansion?
(a) \frac{31}{3125}
(b) \frac{71}{512}
(c) \frac{23}{200}
(d) None of these
Question.16. When 2^{256} is divided by 17 the remanider would be
(a) 1
(b) 16
(c) 14
(d) None of these
Ans.15. (d) None of these
Explanation: 3125, 512 and 200 has factorization of the form 2^{m}\times 5^{n} (where m and n are whole numbers). So given fractions has terminating decimal expansion.
Ans.16. (a) 1
Explanation: When 2^{256} is divided by 17 then,
\frac{2^{256}}{2^{4}+1}=\frac{(2^{2})^{64}}{2^{4}+1}
By remainder theorem when f(x) is divided by x+a the remainder =f(-a)
Here, f(a)=(2^{2})^{64} and x=2^{4} and a=1
Hence, Remainder =f(-1)=(-1)^{64}=1
Question.17. The least number which when divided by 15, leaves a remainder of 5, when divided by 25, leaves a remainder of 15 and when divided by 35 leaves a remainder of 25, is
(a) 515
(b) 525
(c) 1040
(d) 1050
Question.18. Without Actually performing the long division, the terminating decimal expansion of \frac{51}{1500} is in the form of \frac{17}{2^{n}\times 5^{m}}, then (m+n) is equal to
(a) 2
(b) 3
(c) 5
(d) 8
Ans.17. (a) 515
Explanation: The number is short by 10 for complete division by 15, 25 or 35.
Ans.18. (c) 5
Explanation: We have, \frac{51}{1500}=\frac{17}{500}
Prime factorization of 500=2\times 2\times 5\times 5\times 5 = 2^{2}\times 5^{3}
which is in the form 2^{n}\times 5^{m}
So, it has a terminating decimal expansion.
Now, \frac{51}{1500}=\frac{17}{2^{2}\times 5^{3}}
By comparing, we get n=2 and m=3
⇒ m+n=2+3=5
Question.19. The sum of three non-zero prime numbers is 100. One of them exceeds the other by 36. Then the largest number is
(a) 73
(b) 91
(c) 67
(d) 57
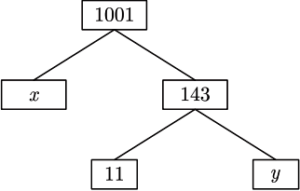
Question.20. The values of x and y is the given figure are
(a) 7, 13
(b) 13, 7
(c) 9, 12
(d) 12, 9
Ans.19. (c) 67
Explanation: Let x, x+36 and y are the three prime numbers.
According to the given condition,
x+x+36+y=100
⇒ 2x+y=64 …(1)
Since x is a prime number, then 2x will be an even number.
Also addition of two even numbers results in an even number.
Hence, from equation (1), we can conclude that y must be an even prime number.
y = 2 as 2 is the only even prime number.
Put y = 2 in equation (1), we get
⇒ 2x+2 = 64
⇒ x = 31x = 31
So the required prime numbers are 31, 31+36, 2 or 31, 67 and 2
Hence, Largest number is 67.
Ans.20. (a) 7, 13
Explanation: Given number is 1001. Then, the factor tree of 1001 is given as below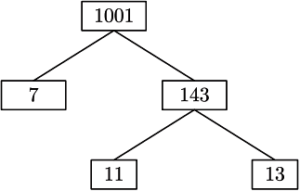
By comparing with given factor tree, we get
x=7, y = 13
Question.21. If P = (2)(4)(6)…(20) and Q = (1)(3)(5)…(19), then the HCF of P and Q is
(a) (3^{3})(5)(7)
(b) (3^{4})(5)
(c) (3^{4})(5^{2})(7)
(d) (3^{3})(5^{2})
Question.22. The number 3^{13}-3^{10} is divisible by
(a) 2 and 3
(b) 3 and 10
(c) 2, 3 and 10
(d) 2, 3 and 13
Ans.21. (c) (3^{3})(5^{2})(7)
Explanation: In P, the primes that occurs are 2, 3, 5, 7.
In Q, there is no 2
So, the HCF of P Q , has powers of only 3, 5 and 7.
In P, 3 comes from 6, 12, 18. So, 3^{4} is the greatest power of 3 in prime factorisation of P . While in Q, 3 comes from 3, 9, 15.
So, 3^{4} is also in prime factorisation of Q.
Similarly 5^{2} is the greatest power of 5 for both P and Q and 7^{1} is the greatest power of 7 for both P and Q.
Hence, HCF of P and Q is (3^{3})(5^{2})(7).
Ans.22. (d) 2, 3 and 13
Explanation: 3^{13}-3^{10}=3^{10}(3^{3}-1)=3^{10}(26)=2\times 13\times 3^{10}
Hence, 3^{13}-3^{10} is divisible by 2, 3 and 13.
Question.23. Which of the following will have a terminating decimal expansion?
(a) \frac{77}{210}
(b) \frac{23}{30}
(c) \frac{125}{441}
(d) \frac{23}{8}
Question.24. For any natural number n, 9^{n} cannot end with the digit.
(a) 1
(b) 2
(c) 9
(d) None of these
Ans.23. (d) \frac{23}{8}
Explanation: For terminating decimal expansion, denominator must have only 2 or only 5 or 2 and 5 as factor.
Here, \frac{23}{8}=\frac{23}{2^{3}}
(only 2 as factor of denominator so terminating)
Ans.24. (b) 2
Explanation: For n=1, 9^{n}=9^{1}=9, so 9^{n} can end with digit 9.
For n=2, 9^{n}=9^{2}=81, so 9^{n} can also end with digit 1.
Now, let if possible 9^{n} ends with 2 for some natural numbers n.
Then, 9^{n} is divisible by 2.
But prime factors of 9 are 3\times 3.
9^{n}=(3\times 3)^{n}=3^{2n}
Thus, prime factorisation of 9^{n} does not contain 2 as a factor.
By the fundamental theorem of arithmetic, there are no other primes in factorisation of 9^{n}.
Therefore, 9^{n} is not divisible by 2. So, our assumption is wrong.
Hence, there is no natural number n for which 9^{n} ends in the digit 2.
Question.25. A number lies between 300 and 400. If the number is added to the number formed by reversing the digits, the sum is 888 and if the unit’s digit and the ten’s digit change places, the new number exceeds the original number by 9. Then the number is
(a) 339
(b) 341
(c) 378
(d) 345
Question.26.
1. The L.C.M. of x and 18 is 36.
2. The H.C.F. of x and 18 is 2.
What is the number x ?
(a) 1
(b) 2
(c) 3
(d) 4
Ans.25. (d) 345
Explanation: Sum is 888
⇒ unit’s digit should add up to 8. This is possible only for option (d) as “3”+“5” =“8”.
Ans.26. (d) 4
Explanation: L.C.M. \times H.C.F. = First number \times second number
Hence, required number = \frac{36\times 2}{18}=4
Question.27. A circular field has a circumference of 360 km. Two cyclists Sumeet and John start together and can cycle at speeds of 12 km/h and 15 km/h respectively, round the circular field. They will meet again at the starting point after
(a) 40 h
(b) 30 h
(c) 180 h
(d) 120 h
Question.28. What is the largest number that divides 70 and 125, leaving remainders 5 and 8 respectively?
(a) 13
(b) 9
(c) 3
(d) 585
Ans.27. (d) 120 h
Explanation: Given, Total distance = 360 km
and, Speed of Sumeet = 12 km/h
Number of hours taken by Sumeet to complete 1 round = \frac{Distance}{Speed}=\frac{360}{12}= 30 h
and, Speed of John = 15 km/h
Number of hours taken by John to complete 1 round = \frac{Distance}{Speed}=\frac{360}{15}= 24 h
Thus, Sumeet and John complete 1 round in 30 h and 24 h, respectively.
Now, to find required hours, we find the LCM of 30 and 24.
⇒ 30=2\times 3\times 5
⇒ 24=2\times 2\times 2\times 3
Then, LCM (30, 24) = 2\times 2\times 2\times 3\times 5 = 120
Hence, Sumeet and John will meet each other again after 120 h.
Ans.28. (a) 13
Explanation: Required number = H.C.F. {(70 – 5), (125 – 8)}
= H.C.F. (65, 117) = 13.
Question.29. What is the largest number that divides 245 and 1029, leaving remainder 5 in each case?
(a) 15
(b) 16
(c) 9
(d) 5
Question.30. A class of 20 boys and 15 girls is divided into n groups so that each group has x boys and y girls. Values of x, y and n respectively are
(a) 3, 4 and 8
(b) 4, 3 and 6
(c) 4, 3 and 7
(d) 7, 4 and 3
Ans.29. (b) 16
Explanation: Required number = H.C.F.{(245 – 5), (1029 – 5)}
= H.C.F. (240, 1024) = 16.
Ans.30. (c) 4, 3 and 7
Explanation: H.C.F. of 20 and 15 = 5
So, 5 students are in each group.
∴ n=\frac{20}{15}=\frac{35}{5}=7
Hence, x = 4, y = 3 and n = 7
Question.31. If p, q are two consecutive natural numbers, then H.C.F. (p, q) is
(a) p
(b) q
(c) 1
(d) pq
Question.32. Given that L.C.M. (91, 26) = 182, then H.C.F. (91, 26) is
(a) 13
(b) 26
(c) 17
(d) 9
Ans.31. (c) 1
Ans.32. (a) 13
Explanation: H.C.F. (91, 126) = \frac{91\times 126}{L.C.M.(91,126)}=\frac{91\times 126}{182}=13
Question.33. Which of the following statement is true?
(a) Every point on the number line represents a rational number.
(b) Irrational numbers cannot be represented by points on the number line.
(c) \frac{22}{7} is a rational number.
(d) None of these.
Question.34. The sum of exponents of prime factors in the prime factorisation of 196 is
(a) 3
(b) 4
(c) 5
(d) 2
Ans.33. (d) None of these.
Explanation: All the given statements are false.
Ans.34. (b)
Explanation: 196=2^{2}\cdot 7^{2}, sum of exponents =2+2=4
Question.35. When a natural number x is divided by 5, the remainder is 2. When a natural number y is divided by 5, the remainder is 4. The remainder is z when x + y is divided by 5. The value of \frac{2z-5}{3} is
(a) –1
(b) 1
(c) –2
(d) 2
Question.36. The largest non-negative integer k such that 24^{k} divides 13! is
(a) 2
(b) 3
(c) 4
(d) 5
Ans.35. (a) -1
Explanation: Since, x is divided by 5, the remainder is 2
therefore x=5m+2
similarly, y=5n+4 consider x+y=5(m+n)+6
= 5(m + n) + 5 + 1
= 5(m + n + 1) + 1
But given that when x+y is divided by 5, the remainder is z
∴ z = 1
Now, \frac{2z-5}{3}=\frac{2(1)-5}{3}=-1
Ans.36. (b) 3
Explanation: We know that
13!=1\times 2\times 3\times 4\times 5\times 6\times 7\times 8\times 9\times 10\times 11\times 12\times 13
= 210\times 35\times 52\times 7\times 11\times 13
⇒ 24^{k}=(2^{3}\times 3)k
where k is largest non-negative integer
When 13! is an divided by 24^{k}, we get
\frac{2^{10}\times 3^{5}\times 5^{2}\times 7\times 11\times 13}{2^{3k}\cdot 3^{k}}
= 2^{10-3k}\times 3^{5-k}\times 5^{2}\times 7\times 11\times 13
∴ 10 – 3k is integer.
Then, maximum value of k = 3.
Question.37. On dividing a natural number by 13, the remainder is 3 and on dividing the same number by 21, the remainder is 11. If the number lies between 500 and 600, then the remainder on dividing the number by 19 is
(a) 4
(b) 6
(c) 9
(d) 13
Question.38. Let a_{1},a_{2},…,a_{100} be non-zero real numbers such that a_{1}+a_{2}+…+a_{100} Then,
(a) \sum_{i=1}^{100}a_{i}2^{a_{i}}>0 and \sum_{i=1}^{100}a_{i}2^{-a_{i}}<0
(b) \sum_{i=1}^{100}a_{i}2^{a_{i}}≥0 and \sum_{i=1}^{100}a_{i}2^{-a_{i}}≥0
(c) \sum_{i=1}^{100}a_{i}2^{a_{i}}≤0 and \sum_{i=1}^{100}a_{i}2^{-a_{i}}≤0
(d) The sign of \sum_{i=1}^{100}a_{i}2^{a_{i}} or \sum_{i=1}^{100}a_{i}2^{-a_{i}} depends on the choice of a_{i}’s
Ans.37. (a) 4
Explanation: Given: The natural number, when divided by 13 leaves remainder 3
The natural number, when divided by 21 leaves remainder 11
So, 13 – 3 = 21 – 11 = 10 = k
Now, LCM (13, 21) = 273
But the number lies between 500 and 600
∴ 2 LCM (13, 21) – k = 546 – 10 = 536
536 = 19\times8+4
∴ remainder = 4
Ans.38. (a) \sum_{i=1}^{100}a_{i}2^{a_{i}}>0 and \sum_{i=1}^{100}a_{i}2^{-a_{i}}<0
Explanation: Let a_{1},a_{2},…,a_{100} be non-zero real number and
a_{1}+a_{2}+…+a_{100}
a_{i}2^{a_{i}}>a_{i} and a_{i}2^{-a_{i}}<a_{i}
∴ \sum_{i=1}^{100}a_{i}2^{a_{i}}>\sum_{i=1}^{100}a_{i} and \sum_{i=1}^{100}a_{i}2^{-a_{i}}<\sum_{i=1}^{100}a_{i}
⇒ \sum_{i=1}^{100}a_{i}2^{a_{i}}>0</span> and \sum_{i=1}^{100}a_{i}2^{-a_{i}}<0
Hence, option (a) is correct.
Question.39. The value of 0.\overline{235} is :
(a) \frac{233}{900}
(b) \frac{233}{990}
(c) \frac{235}{999}
(d) \frac{235}{990}
Question.40. Consider the following statements: For any integer n,
I. n^{2}+3 is never divisible by 17.
II. n^{2}+4 is never divisible by 17.
Then,
(a) both I and II are true
(b) both I and II are false
(c) I is false and II is true
(d) I is true and II is false
Ans.39. (c) \frac{235}{999}
Explanation: Let x=0.\overline{235} …(i)
1000x=235.\overline{235} …(ii)
Subtract (i) from (ii),
999x=235
⇒ x=\frac{235}{999}
Ans.40. (d) I is true and II is false
Explanation: Let us consider that n^{2}+3 is divisible by 17
∴ n^{2}+3=17K K ∈ N
⇒ n^{2}=17K-3
⇒ n^{2}=3(17m-1) [∵ K = 3m]
3(17m – 1) is a perfect square, which is not possible.
∴ n^{2}+3 is never divisible by 17.
In, n^{2}+4, put n = 9
So, (9)^{2}+4=81+4=85 which is divisible by 17.
∴ I is true and II is false.
Question.41. Given that \frac{1}{7}=0.\overline{142857}, which is a repeating decimal having six different digits. If x is the sum of such first three positive integers n such that \frac{1}{n}=0.\overline{abcdef}, where a, b, c, d, e and f are different digits, then the value of x is
(a) 20
(b) 21
(c) 41
(d) 42
Question.42. If m=n^{2}-n, where n is an integer, then m^{2}-2m is divisible by
(a) 20
(b) 24
(c) 30
(d) 16
Ans.41. (c) 41
Explanation: \frac{1}{7}=0.\overline{142857}
The second positive integer whose reciprocal have six different repeating decimals is
\frac{1}{13}=0.\overline{076923}
And the third positive integer whose reciprocal have six different repeating decimals is
\frac{1}{21}=0.\overline{047619}
Therefore, the values of x are 7, 13, 21
Hence, the required sum is = 7 + 13 + 21 = 41
Ans.42. (b) 24
Explanation:
∵m=n^{2}-n=n(n – 1)
Now, m^{2}-2m=m(m – 2)
= n(n – 1)(n^{2}-n-2)
= n(n – 1)(n-2)(n+1)
Since we know that product of any four consecutive integers is always divisible by 24.
∴ m^{2}-2m is divisible by 24.
Question.43. The unit digit in the expression 55^{725}+73^{5810}+22^{853} is
(a) 0
(b) 4
(c) 5
(d) 6
Question.44. For some integer m, every even integer is of the form
(a) m
(b) m+1
(c) 2m
(d) 2m+1
Ans.43. (d) 6
Explanation: For given numbers,
55^{725}, unit digit = 5;
73^{5810}, unit digit = 9
22^{853}, unit digit = 2
Unit digit in the expression 55^{725}+73^{5810}+22^{853} is 6
Ans.44. (c) 2m
Question.45. For some integer q, every odd integer is of the form
(a) q
(b) q+1
(c) 2q
(d) 2q+1
Question.46. The decimal expansion of the rational number \frac{33}{2^{2}\cdot5} will terminate after
(a) one decimal place
(b) two decimal places
(c) three decimal places
(d) more than 3 decimal places
Ans.45. (d) 2q+1
Ans.46. (b) two decimal places
Question.47. Product of two co-prime numbers is 117. Their L.C.M. should be
(a) 1
(b) 117
(c) equal to their H.C.F.
(d) Lies between 1 to 117
Question.48. Which of the following statement(s) is/are always true?
(a) The sum of two distinct irrational numbers is rational.
(b) The rationalising factor of a number is unique.
(c) Every irrational number is a surd.
(d) None of these
Ans.47. (b) 117
Explanation: Since, H.C.F. of co-prime number is 1.
∴ Product of two co-prime numbers is equal to their L.C.M. So, L.C.M. = 117
Ans.48. (d) None of these
Question.49. Which of the following statement(s) is/are not correct?
(a) \frac{7^{3}}{5^{4}} is a non-terminating repeating decimal.
(b) If a=2+\sqrt{3} andb=\sqrt{2}-\sqrt{3}, then a + b is irrational.
(c) If 19 divides a^{3}, then 19 divides a, where a is a positive integer.
(d) Product of L.C.M. and H.C.F. of 25 and 625 is 15625.
Question.50. The product of unit digit in (7^{95}-3^{58}) and (7^{95}+3^{58}) is
(a) 8
(b) lies between 3 and 7
(c) 6
(d) lies between 3 and 6
Ans.49. (a) \frac{7^{3}}{5^{4}} is a non-terminating repeating decimal.
Ans.50. (a)
Explanation: Unit digit in 7^{95} = Unit digit in (7^{4})^{23}\times 7^{3}
= Unit digit in 7^{3} (as unit digit in 7^{4}=1)
= Unit digit in 343
Unit digit in 3^{58} = Unit digit in (3^{4})^{4}\times 3^{2}
[as unit digit 3^{4}=1]
= Unit digit is 9
So, unit digit in (7^{95}-3^{58})
= Unit digit in (343 – 9) = Unit digit in 334 = 4
Unit digit in (7^{95}+3^{58}) = Unit digit in (343 + 9)
= Unit digit in 352 = 2
So, the product is 4\times 2=8