Very Short Answers Maths Class 10 Chapter 1 Real Numbers

Fill in the blanks

Question.1. H.C.F. of 6, 72 and 120 is ________.

Question.2. 156 as a product of its prime factors __________.

Question.3. If $a=bq+r$ , least value of $r$ is ________.

Question.4. If every positive even integer is of the form $2q$ , then every positive odd integer is of the form __________, where $q$ is some integer.

Question.5. The exponent of 2 in the prime factorisation of 144, is _________.

Answer

Ans.1. 6
Ans.2. $2^{2}\times 3 \times 13$
Ans.3. Zero
Ans.4. $2q+1$
Ans.5. 4

Question.6. $\sqrt{2}$ , $\sqrt{3}$ , $\sqrt{7}$ , etc. are _______ numbers.

Question.7. $7\sqrt{5}$ is a/an ________ number.

Question.8. An algorithm which is used to find HCF of two positive numbers is __________.

Question.9. $6+\sqrt{2}$ is a/an __________ number.

Question.10. Every point on the number line corresponds to a _________ number.

Answer

Ans.6. Irrational
Ans.7. irrational
Ans.8. Euclid’s division algorithm
Ans.9. irrational
Ans.10. Real

Question.11. A _________ is a proven statement used for proving another statement.

Question.12. The product of three numbers is _________ to the product of their HCF and LCM.

Question.13. L.C.M. of 96 and 404 is __________.

Question.14. If $p$ is a prime number and it divides $a^{2}$ then it also divides _________, where $a$ is a positive integer.

Question.15. $\frac{35}{50}$ is a ________ decimal expansion.

Answer

Ans.11. lemma
Ans.12. Not equal
Ans.13. 9696
Ans.14. $a$
Ans.15. terminating

Question.16. An ________ is a series of well defined steps which gives a procedure for solving a type of problem.

Question.17. Every real number is either a _______ number or an __________ number.

Question.18. $\frac{1}{\sqrt{2}}$ is a/an __________ number.

Question.19. Numbers having non-terminating, non-repeating decimal expansion are known as ________.

Question.20. $\sqrt{5}$ is a/an _________ number.

Answer

Ans.16. algorithm
Ans.17. Rational, irrational
Ans.18. irrational
Ans.19. Irrational numbers
Ans.20. irrational

True / False

Question.1. Given positive integers $a$ and $b$ , there exist whole numbers $q$ and $r$ satisfying $a=bq+r$ , $0\leqr<b$ .

Question.2. HCF of two numbers is always a factor of their LCM.

Question.3. Every composite number can be expressed (factorised) as a product of primes, and this factorisation is unique, apart from the order in which the prime factors occur.

Question.4. Sum of two prime numbers is always a prime number.

Question.5. The number zero is irrational.

Answer

Ans.1. True
Ans.2. True
Ans.3. True
Ans.4. False
Ans.5. False

Question.6. $\sqrt{2}$ and $\sqrt{3}$ are irrationals numbers.

Question.7. π is an irrational number.

Question.8. Some irrational numbers are negative.

Question.9. If $x=\frac{p}{q}$ be a rational number, such that the prime factorisation of $q$ is not of the form $2^{n}5^{m}$ , where $n$ , $m$ are non-negative integers. Then $x$ has a decimal expansion which is terminates.

Question.10. All real numbers are rational numbers.

Answer

Ans.6. True
Ans.7. True
Ans.8. True
Ans.9. False
Ans.10. False

Question.11. Any positive odd integer is of the form $6q+1$ , or $6q+3$ , or $6q+5$ , where $q$ is some integer.

Question.12. Sum of two irrational numbers is an irrational number.

Question.13. The quotient of two integers is always a rational number.

Question.14. Two numbers can have 12 as their LCM and 350 as their HCF.

Question.15. 1/0 is not rational.

Answer

Ans.11. True
Ans.12. False
Ans.13. False
Ans.14. False
Ans.15. True

Question.16. The product of any three consecutive natural numbers is divisible by 6.

Question.17. If $x=\frac{p}{q}$ be a rational number, such that the prime factorisation of $q$ is of the form $2^{n}5^{m}$ , where $n$ , $m$ are non-negative integers. Then $x$ has a decimal expansion which is terminates.

Question.18. All integers are real numbers.

Question.19. The number of irrational numbers between 15 and 18 is infinite.

Question.20. Every fraction is a rational number.

Answer

Ans.16. True
Ans.17. True
Ans.18. True
Ans.19. True
Ans.20. True

Match the Columns

Each question contains statements given in two columns which have to be matched. Statements (A, B, C, D) in column I have to be matched with statements (p, q, r, s) in column II.

Question.1.

Answer

Ans.1. (A)-r, (B)-s, (C)-p, (D)-q

Question.2.

Answer

Ans.2. (A)-r, (B)-p, (C)-q

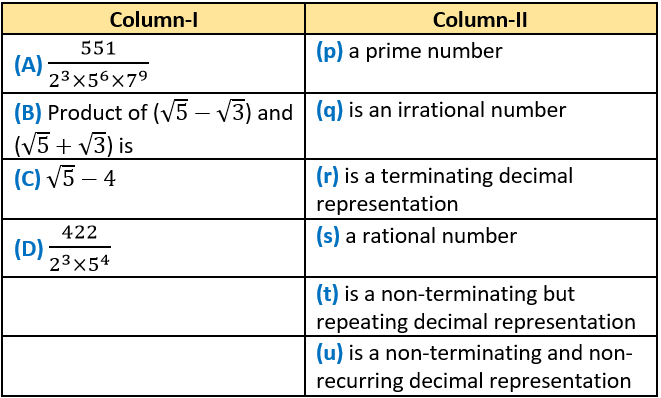
Question.3.

Answer

Ans.3. (A)-(t, s), (B)-(p, s), (C)-(q, u), (D)-(r, s)

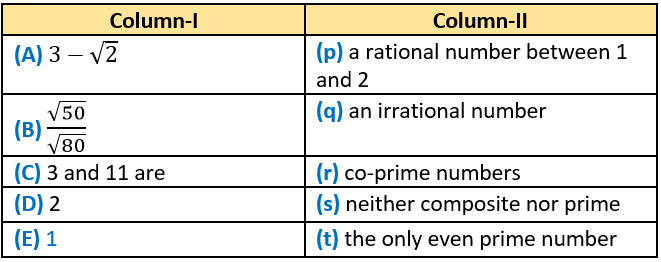
Question.4.

Answer

Ans.4. (A)-q, (B)-p, (C)-r, (D)-t, (E)-s