What is Case Study Question / Paragraph Based Question?
A case study is a scenario in a particular academic / professional context which students are expected to analyse and respond to, guided by specific questions posed concerning the situation. In many cases, the scenario or case study involves a number of issues or problems that must be dealt with in a academic / professional workplace.
Why Case Study Questions are included in academics?
Case study assignments usually require students to identify problems and issues in a scenario, to demonstrate their developing knowledge of theories and academic / professional policies and to make decisions and recommendations based on these to either prevent or solve some of the issues in that scenario.
How to solve Case Study Questions?
There are several steps to writing an answer to a case study assignment:
STEP 1: Read the case study and questions carefully.
- Read the case and associated questions carefully.
- Highlight the main points of the case and any issues that you can identify.
- Read the questions closely and analyse what they are requiring you to do.
- Read the case again, linking the information that is relevant to each question you have been asked.
STEP 2: Identify the issues in the case study.
Case studies describe a situation which may arise in a particular profession or social context. They often involve a number of people in a complex situation. They will often describe a situation which is problematic, possibly in how it is dealt with, or in its complexity. An important part of your answer is to analyse the situation and to identify the issues/actions described in the case which may be problematic. The following questions may help you to do this:
- What actions were taken in the case?
- Were these actions the most appropriate and why?
- Were there any consequences of the actions taken?
- Was anything omitted or not considered?
- Were actions/procedures in line with existing codes of practice, policy or theories?
STEP 3: Link theory to practice.
Use your knowledge of existing codes of practice, theories and/or other academic / professional documents and behaviours to decide what was done appropriately and what was not.
STEP 4: Plan your answer.
It can be useful to use the questions you have been set as headings and to answer each part in turn, reducing the chance of omitting set questions. You can always take out the headings before you submit if you wish. Lecturers usually set questions in a logical order, so answer in the order they are written in your question.
STEP 5: Start writing your case study answer (for theory only)
Like any assignment, you will need an introduction, body sections in which you answer the questions put to you regarding the case study, and a conclusion.
STEP 6: Edit and proofread.
Read through your paper yourself to detect and correct other errors and omissions.
Check you have answered all questions and backed up your answer with relevant passage.
Types of Case Study Questions / Paragraph Based Questions
Case Study Questions / Paragraph Based Questions can be broadly classified into two types:
- MCQs type: In this type, student has to tick the correct option from various options.
- Theory type: In this type, student has to write proper solution / answer in cotext to the case study.
Case Study/ Passage Based Questions Chapter 8 Introduction to Trigonometry Mathematics
Type 1: MCQ type
Case Study Question 01
Read the following and answer any four questions from 1 to 4 given below:
Doing swing ball in a cricket match turns the ball and can put the batsman in danger. Our two famous bowlers Ashwin and Akash, throws the ball at an angle of A and B respectively. The relation between A and B are such that Sin (A-B) = \frac{1}{2} and cos (A+B) = 0, 0°< A+B ≤ 90°, A>B.
Question.1. What is the measure of \angle A?
(a) 30°
(b) 45°
(c) 60°
(d) 90°
Question.2. What is the measure of \angle B?
(a) 30°
(b) 45°
(c) 60°
(d) 90°
Question.3. Now on the bases of value of A and B derived find cosec (A-B)
(a) 0
(b) 2
(c) \sqrt{2}
(d) \frac{2}{\sqrt{3}}
Question.4. What is the value of sec B?
(a) 0
(b) 1
(c) ∞
(d) \frac{2}{\sqrt{3}}
Question.5. If Sin θ = \frac{a}{b} , then Cos θ is equal to:
(a) \frac{b}{\sqrt{b^{2}-a^{2}}}
(b) \frac{b}{a}
(c) \frac{a}{\sqrt{b^{2}-a^{2}}}
(d) \frac{\sqrt{b^{2}-a^{2}}}{a}
Ans.1. (c)
60°
Ans.2. (a)
30°
Ans.3. (b)
2
Ans.4. (d)
\frac{2}{\sqrt{3}}
Ans.5. (d)
\frac{\sqrt{b^{2}-a^{2}}}{a}
Case Study Question 02
Read the following and answer any four questions from 1 to 5 given below:
In the month of November, Akshay notices a tower built near his colony’s playground. He sees that it is being held by a wire, attached to the top of the tower. The wire makes an angle of 60° with the ground. 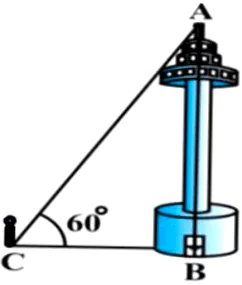
Question.1. What is the measure of \angleCAB?
(a) 15°
(b) 25°
(c) 30°
(d) 45°
Question.2. What is the sin ratio of \angleCAB?
(a) 0
(b) \frac{1}{2}
(c) \frac{1}{\sqrt{2}}
(d) \frac{\sqrt{3}}{2}
Question.3. What is the value of cos \angleACB?
(a) 0
(b) \frac{1}{2}
(c) \frac{1}{\sqrt{2}}
(d) \frac{\sqrt{3}}{2}
Question.4. \sin^{2}\angle CAB+\cos^{2}\angle CAB =
(a) 0
(b) 1
(c) 2
(d) 3
Question.5. What is the value of tan 90°?
(a) 0
(b) 1
(c) \frac{1}{2}
(d) not defined
Ans.1. (c)
30°
Ans.2. (b)
\frac{1}{2}
Ans.3. (b)
\frac{1}{2}
Ans.4. (b)
1
Ans.5. (d)
not defined
Case Study Question 03
Read the following and answer any four questions from 1 to 5 given below:
Mohan, a class X student is a big foodie. Once his mother has made a sandwich for him. A thought has come into his mind by seeing a piece of sandwich. He thought if he increases the base length and height, he can eat a bigger piece of sandwich.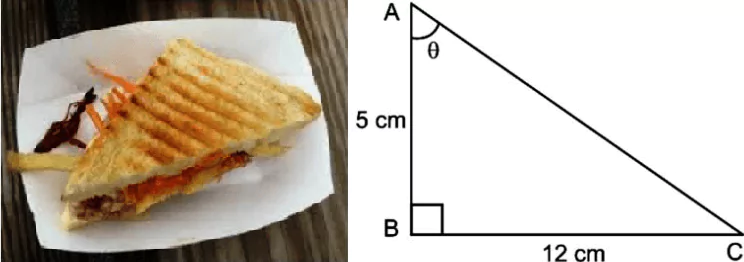
Question.1. If the length of the base is 12 cm and the height is 5 cm then the length of the hypotenuse of that sandwich is:
(a) 17 cm
(b) 7 cm
(c) 169 cm
(d) 13 cm
Question.2. What will be the value of cosine of the angle between hypotenuse and the height of sandwich?
(a) \frac{5}{13} cm
(b) \frac{12}{13} cm
(c) \frac{13}{5} cm
(d) \frac{13}{12} cm
Question.3. If he increases the base length to 15 cm and the hypotenuse to 17 cm, then the height of the sandwich is :
(a) 7 cm
(b) 8 cm
(c) 32 cm
(d) none of these
Question.4. If the value of tan θ is \sqrt{3} , then sin θ equals to:
(a) \frac{1}{\sqrt{2}}
(b) \frac{\sqrt{3}}{2}
(c) \frac{1}{2}
(d) 1
Question.5. The value of tan 45° + cot 45°
(a) 1
(b) 2
(c) 3
(d) 4
Ans.1. (d)
13 cm
Ans.2. (a)
\frac{5}{13} cm
Ans.3. (b)
8 cm
Ans.4. (b)
\frac{\sqrt{3}}{2}
Ans.5. (b)
2
Case Study Question 04
Read the following and answer any four questions from 1 to 5 given below:
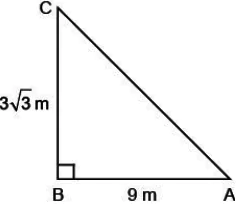
Three friends Ashwin, Bhagath & Amal are playing hide and seek in a park. Ashwin, Bhagath hide in the shrubs and Amal have to find both of them. If the positions of three friends are at A, B and C respectively as shown in the figure and forms a right-angled triangle, such that AB = 9 m, BC = 3\sqrt{3} m and \angleB = 90°.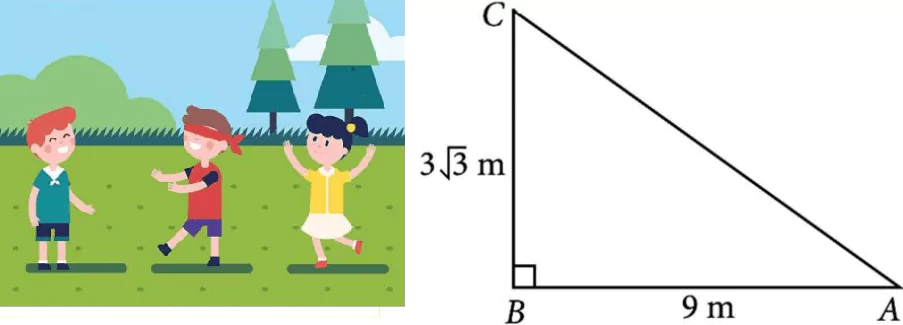
On the basis of above answer the following questions:
Question.1. The measure of \angleA is
(a) 30°
(b) 45°
(c) 60°
(d) 90°
Question.2. The measure of \angleC is
(a) 30°
(b) 45°
(c) 60°
(d) 90°
Question.3. The length of AC is
(a) 8\sqrt{2}
(b) 6\sqrt{3}
(c) 4\sqrt{2}
(d) 2\sqrt{3}
Question.4. cos 2A =
(a) 0
(b) \frac{1}{2}
(c) \frac{1}{\sqrt{2}}
(d) \frac{\sqrt{3}}{2}
Question.5. \sin \left(\frac{C}{2}\right) =
(a) 0
(b) \frac{1}{2}
(c) \frac{1}{\sqrt{2}}
(d) \frac{\sqrt{3}}{2}
Ans.1. (a) 30°
We have AB = 9 m and BC = 3\sqrt{3} m
In ∆ABC, we have
⇒ tan A = \frac{BC}{AB} = \frac{3\sqrt{3}}{9} = \frac{1}{\sqrt{3}}
⇒ tan A = tan 30°
∴ \angleA = 30°
Ans.2. (c) 60°
Similarly, tan C = \frac{AB}{BC} = \frac{9}{3\sqrt{3}} = \sqrt{3}
⇒ tan A = tan 60°
∴ \angleC = 60°
Ans.3. (b) 6\sqrt{3} m
Since, sin A = \frac{BC}{AC}
⇒ sin 30° = \frac{BC}{AC}
⇒ \frac{1}{2} = \frac{3\sqrt{3}}{AC}
⇒ AC = 6\sqrt{3} m
Ans.4. (b) \frac{1}{2}
From ans (i), \angleA = 30°
∴ cos 2A = cos(2✕30°) = cos 60° = \frac{1}{2}
Ans.5. (b) \frac{1}{2}
From ans (ii), \angleC = 60°
∴ sin \left(\frac{C}{2}\right) = sin \left(\frac{60}{2}\right) = sin 30° = \frac{1}{2}
Case Study Question 05
Read the following and answer any four questions from 1 to 5 given below:
Two aeroplanes leave an airport, one after the other. After moving on runway, one flies due North and other flies due South. The speed of two aeroplanes are 400 km/hr and 500 km/hr respectively. Considering PQ as runway and A and B are any points in the path followed by two planes.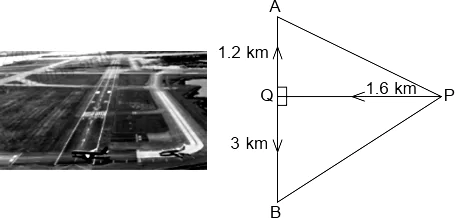
Question.1. Find tan θ, if \angleAPQ = θ
(a) \frac{3}{4}
(b) \frac{1}{2}
(c) \frac{1}{\sqrt{2}}
(d) \frac{\sqrt{3}}{2}
Question.2. Find the value of cot B
(a) \frac{3}{4}
(b) \frac{15}{4}
(c) \frac{3}{8}
(d) \frac{15}{8}
Question.3. Find the value of tan A
(a) \frac{3}{4}
(b) \frac{4}{3}
(c) \frac{1}{\sqrt{2}}
(d) \frac{\sqrt{3}}{2}
Question.4. Find the value of sec A
(a) 0
(b) \frac{5}{3}
(c) \frac{1}{\sqrt{2}}
(d) \frac{\sqrt{3}}{2}
Question.5. Find cosec B
(a) \frac{17}{8}
(b) \frac{8}{17}
(c) \frac{12}{5}
(d) \frac{5}{12}
Ans.1. (a)
In ∆APQ, we have
⇒ tan θ = \frac{AQ}{PQ} = \frac{1.2}{1.6} = \frac{3}{4}
Ans.2. (d)
In ∆PBQ, we have
⇒ cot θ = \frac{QB}{PQ} = \frac{3}{1.6} = \frac{15}{8}
Ans.3. (b)
In ∆APQ, we have
⇒ tan A = \frac{PQ}{AQ} = \frac{1.6}{1.2} = \frac{4}{3}
Ans.4. (b)
We know that, \tan^{2}A+1=\sec^{2}A
⇒ \sec^{2}A = \sqrt{\left(\frac{4}{3}\right)^{2}+1} = \sqrt{\frac{16}{9}+1} = \sqrt{\frac{25}{9}} = \frac{5}{3}
Ans.5. (a)
We know that, cot^{2}B+1=cosec^{2}B
⇒ cosec^{2}B = \sqrt{\left(\frac{15}{8}\right)^{2}+1} = \sqrt{\frac{289}{64}} = \frac{17}{8}
Case Study Question 06
Read the following and answer any four questions from 1 to 5 given below:
Raji a student of class 10, has to made a project on ‘Introduction to Trigonometry.’ She decides to make a bird house which is triangular in shape. She uses cardboard to make the bird house as shown in the figure. Considering the front side of bird house as a right-angled triangle PQR, right angled at R, answer the following questions.
Question.1. If \anglePQR = θ, the cos θ =
(a) \frac{12}{13}
(b) \frac{13}{12}
(c) \frac{12}{5}
(d) \frac{5}{12}
Question.2. Find the value of sec θ
(a) \frac{12}{13}
(b) \frac{13}{12}
(c) \frac{12}{5}
(d) \frac{5}{12}
Question.3. Find the value of \frac{\tan \theta}{1+\tan^{2}\theta}
(a) \frac{60}{169}
(b) \frac{169}{60}
(c) \frac{12}{5}
(d) \frac{5}{12}
Question.4. The value of \cot^{2}\theta-cosec^{2}\theta
(a) 0
(b) 1
(c) 2
(d) -1
Question.5. The value of \sin^{2}\theta+\cos^{2}\theta
(a) 0
(b) 1
(c) 2
(d) -1
Ans.1. (a)
cos θ = \frac{RQ}{PQ} = \frac{12}{13}
Ans.2. (b)
The value of sec θ = \frac{1}{cos θ} = \frac{13}{12}
Ans.3. (a)
In rt. ∆PQR,
PR^{2}+RQ^{2}=PQ^{2} ..[Pythagoras’ theorem]
⇒ PR^{2}=(13)^{2}-(12)^{2} = 25
⇒ PR = 5 cm
tan θ = \frac{PR}{RQ} = \frac{5}{12}
∴ \frac{\tan \theta}{1+\tan^{2}\theta} = \frac{\frac{5}{12}}{1+\frac{25}{144}} = \frac{\frac{5}{12}}{\frac{169}{144}} = \frac{60}{169}
Ans.4. (d)
As we know, cosec^{2}θ-cot^{2}θ=1
⇒ –( cot^{2}θ-cosec^{2}θ ) = 1
∴ cot^{2}θ-cosec^{2}θ = –1
Ans.5. (b)
1
Case Study Question 07
Read the following and answer any four questions from 1 to 5 given below:
Raj is an electrician in a village. One day power was not there in entire village and villagers called Raj to repair the fault. After thorough inspection he found an electric fault in one of the electric pole of height 5 m and he has to repair it. He needs to reach a point 1.3 m below the top of the pole to undertake the repair work.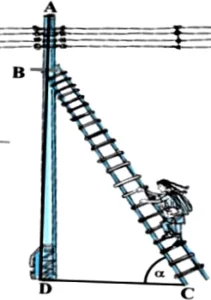
Question.1. When the ladder is inclined at an angle of α such that \sqrt{3} \tan \alpha +2=5 to the horizontal, find the angle α.
(a) 30°
(b) 45°
(c) 60°
(d) 90°
Question.2. How far from the foot of the pole should he place the foot of the ladder? (Use \sqrt{3} = 1.73)
(a) 2.89 m
(b) 2.14 m
(c) 3 m
(d) none of these
Question.3. In the above situation, find the value of \sin \alpha \cos \frac{\alpha}{2}-\cos \alpha \sin \frac{\alpha}{2}
(a) 0
(b) 1
(c) \frac{1}{2}
(d) none of these
Question.4. In the above situation if BD = 3 cm and BC = 6 cm. Find α
(a) 45°
(b) 30°
(c) 60°
(d) none of these
Question.5. If 15 cot α = 8. The value of sin α is
(a) \frac{17}{15}
(b) \frac{15}{17}
(c) \frac{15}{8}
(d) \frac{8}{17}
Ans.1. (c)
60°
Ans.2. (b)
2.14 m
Ans.3. (c)
\frac{1}{2}
Ans.4. (b)
30°
Ans.5. (b)
\frac{15}{17}
Case Study Question 08
Read the following and answer any four questions from 1 to 5 given below:
Ritu’s daughter is feeling so hungry and so thought to eat something. She looked into the fridge and found some bread pieces. She decided to make a sandwich. She cut the piece of bread diagonally and found that it forms a right-angled triangle with sides 4 cm, 4\sqrt{3} cm and 8 cm.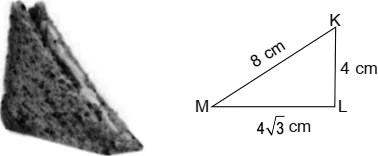
Question.1. The value of \angleM =
(a) 30°
(b) 60°
(c) 45°
(d) None of these
Question.2. The value of \angleK =
(a) 45°
(b) 30°
(c) 60°
(d) None of these
Question.3. Find the value of cot M.
(a) \sqrt{3}
(b) \frac{1}{\sqrt{3}}
(c) 1
(d) None of these
Question.4. sec^{2}M-1 =
(a) tan M
(b) tan 2M
(c) \tan^{2}M
(d) None of these
Question.5. The value of \frac{\tan^{2}45°-1}{\tan^{2}45°+1} is
(a) 0
(b) 1
(c) 2
(d) –1
Ans.1. (a)
tan M = \frac{KL}{LM} = \frac{4}{4\sqrt{3}} = \frac{1}{\sqrt{3}}
⇒ tan M = tan 30°
⇒ \angleM = 30°
Ans.2. (c) 60°
tan K = \frac{ML}{KL} = \frac{4\sqrt{3}}{4} = \sqrt{3}
⇒ tan K = tan 60°
⇒ \angleK = 60°
Ans.3. (a)
We have, \angleM = 30°
∴ cot M = cot 30° = \sqrt{3}
Ans.4. (c)
\tan^{2}M
Ans.5. (a)
\frac{\tan^{2}45°-1}{\tan^{2}45°+1} = \frac{(1)^{2}-1}{(1)^{2}+1} = \frac{0}{2} = 0
[ ∵ tan 45° = 1]
Case Study Question 09
Read the following and answer any four questions from 1 to 4 given below:
Aanya and her father go to meet her friend Juhi for a party. When they reached Juhi’s place, Aanya saw the roof of the house which is triangular in shape.
Question.1. If D is the mid point of AC, then BD =
(a) 2 m
(b) 3 m
(c) 4 m
(d) 6 m
Question.2. Measure of \angleA =
(a) 30°
(b) 60°
(c) 45°
(d) None of these
Question.3. Measure of \angleC =
(a) 30°
(b) 60°
(c) 45°
(d) None of these
Question.4. Find the value of sin A + cos C.
(a) 0
(b) 1
(c) \frac{1}{\sqrt{2}}
(d) \sqrt{2}
Question.5. Find the value of \tan^{2}C+\tan^{2}A .
(a) 0
(b) 1
(c) 2
(d) \frac{1}{2}
Ans.1. (d)
We have, AB = BC = 6\sqrt{2} m & AC = 12 m
∵ D is mid-point of AC.
∴ AD = DC = 6 m
Now, AB^{2}=BD^{2}+AD^{2} (∵ ∆ABD is a right triangle)
⇒ BD^{2}=(6\sqrt{2})^{2}-6^{2} = 72 – 36 = 36
⇒ BD = 6 m
Ans.2. (c)
In ∆ABD, sin A = \frac{BD}{AB} = \frac{6}{6\sqrt{2}} = \frac{1}{\sqrt{2}}
⇒ sin A = sin 45°
∴ \angleA = 45°
Ans.3. (c)
Explanation: In ∆BDC, tan C = \frac{BD}{DC} = \frac{6}{6}
⇒ tan C = 1 = tan 45°
∴ \angleC = 45°
Ans.4. (d)
sin A = \frac{1}{\sqrt{2}} and
cos C = cos 45° = \frac{1}{\sqrt{2}}
∴ sin A + cos C = \frac{1}{\sqrt{2}}+ \frac{1}{\sqrt{2}} = \frac{2}{\sqrt{2}} = \sqrt{2}
Ans.5. (c)
tan C = 1, tan A = tan 45° = 1
∴ \tan^{2}C+\tan^{2}A = 1 + 1 = 2
Case Study Question 10
Read the following and answer any four questions from 1 to 5 given below:
Three children were playing with sticks. As they had one stick each of them, they put all the three sticks together. Finding all the three sticks equal, they pick up the sticks and put them in a triangular form in such a way that the ends of each stick touch the other. They were surprised. Now they thought of a plane. They took another stick and put it as in the adjacent figure. The stick AD is just touching the stick BC. Somehow, they measured each angle. Finding that each angle. \angleA = \angleB = \angleC = 60° (equal) and \angleBAD = \angleCAD = 30°. Likewise, they measured BD = CD, and \angleADB = \angleADC = 90°.
Taking AB = BC = CA = 2a, you are required to answer the following questions:
Question.1. The length of AD is
(a) a
(b) 2a
(c) \sqrt{2} a
(d) \sqrt{3} a
Question.2. Using the above figure, the value of sin 30° is
(a) \frac{1}{2}
(b) \frac{1}{\sqrt{2}}
(c) \frac{\sqrt{3}}{2}
(d) 1
Question.3. Using the above figure, the value of cos 60° is
(a) 0
(b) 1
(c) \frac{1}{2}
(d) \frac{\sqrt{3}}{2}
Question.4. Using the above figure, the value of tan 30° is
(a) \sqrt{3}
(b) 1
(c) 0
(d) \frac{1}{\sqrt{3}}
Question.5. Using the above figure, the value of cosec 60° is
(a) \frac{2}{\sqrt{3}}
(b) \frac{\sqrt{3}}{2}
(c) \frac{1}{2}
(d) \frac{1}{\sqrt{2}}
Ans.1. (d)
\sqrt{3}a
Ans.2. (a)
\frac{1}{2}
Ans.3. (c)
\frac{1}{2}
Ans.4. (d)
\frac{1}{\sqrt{3}}
Ans.5. (a)
\frac{2}{\sqrt{3}}
Case Study Question 11
Read the following and answer any four questions from 1 to 4 given below:
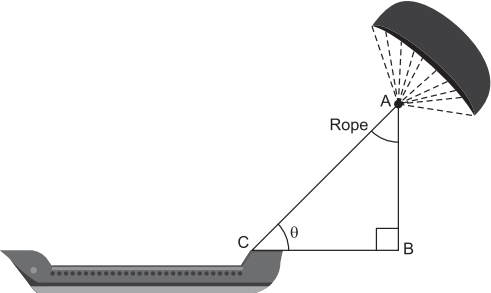
Skysails’ is that genre of engineering science that uses extensive utilization of wind energy to move a vessel in the sea water. The ‘Skysails’ technology allows the towing kite to gain a height of anything between 100 metres to 300 metres. The sailing kite is made in such a way that it can be raised to its proper elevation and then brought back with the help of a ‘telescopic mast’ that enables the kite to be raised properly and effectively.
Question.1. In the given figures, if sin θ = cos (3θ – 30°), where θ and 3θ – 30° are acute angles, then the value of θ is
(a) 30°
(b) 60°
(c) 45°
(d) None of these.
Question.2. What should be the length of the rope of the kite sail in order to pull the ship at the angle θ (calculated in part (a) and be at a vertical height of 200 m?
(a) 300 m
(b) 400 m
(c) 500 m
(d) 600 m
Question.3. If BC = 15 m, θ = 30°, then AB is
(a) 2\sqrt{3} m
(b) 15 m
(c) 24 m
(d) 5\sqrt{3} m
Question.4. Suppose AB = BC = 12 m, then θ =
(a) 0°
(b) 30°
(c) 45°
(d) 60°
Question.5. Given that BC = 6 m and q = 45°. The values of AB and AC are respectively
(a) AB = 4 m, AC = 4\sqrt{2} m
(b) AB = 7 m, AC = 7\sqrt{5} m
(c) AB = 9 m, AC = 9\sqrt{3} m
(d) AB = 6 m, AC = 6\sqrt{2} m
Ans.1. (a)
30°
Ans.2. (b)
400 m
Ans.3. (d)
5\sqrt{3} m
Ans.4. (c)
45°
Ans.5. (d)
AB = 6 m, AC = 6\sqrt{2} m
Case Study Question 12
Read the following and answer any four questions from 1 to 5 given below:
In ∆ABC, right angled at B.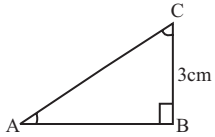
Question.1. The value of cot C is
(a) \frac{3}{4}
(b) \frac{1}{4}
(c) \frac{5}{4}
(d) None of these
Question.2. The value of sec C is
(a) \frac{4}{3}
(b) \frac{5}{3}
(c) \frac{1}{3}
(d) None of these
Question.3. \sin^{2}C+\cos^{2}C =
(a) 0
(b) 1
(c) –1
(d) None of these
In ∆ABC, by Pythagoras theorem,
AC^{2}=AB^{2}+BC^{2}
⇒ AB = 4 cm.
AC = 5 cm.
Ans.1. (a)
Cot C = \frac{BC}{AB} = \frac{3}{4}
Ans.2. (b)
sec C = \frac{AC}{BC} = \frac{5}{3}
Ans.3. (b)
sin C = \frac{4}{5} ,
cos C = \frac{3}{5}
So, \sin^{2}C+\cos^{2}C = \left(\frac{4}{5}\right)^{2}+\left(\frac{3}{5}\right)^{2} = \frac{16+9}{25} = \frac{25}{25} = 1
Case Study Question 13
Read the following and answer any four questions from 1 to 5 given below:
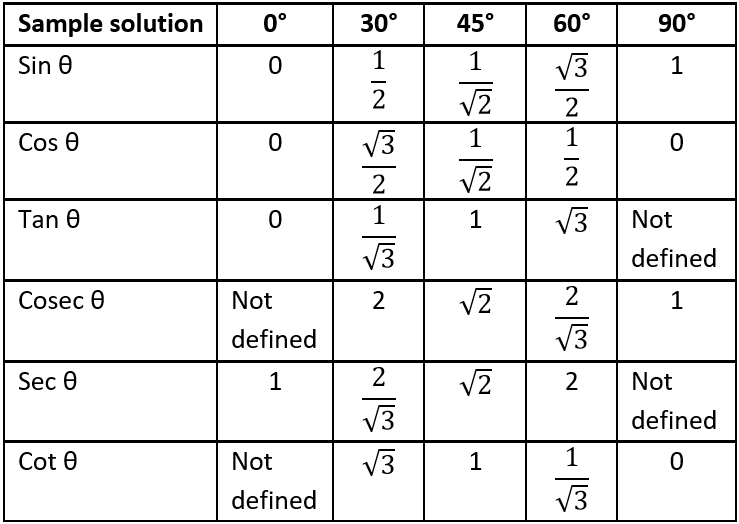
There are in total six trigonometric ratios, namely sine (sin), cosine(cos), tangent (tan), cosecant (cosec), secant (sec) and cotangent (cot). The trigonometric functions cosecant, secant and cotangent are simply the reciprocals of the trigonometric functions sine, cosine and tangent for the angles of a triangle. The values of these trigonometric ratios gives a certain rational for some values of angle (say θ). Some such values for the angle of triangle are shown in the table below:
Question.1. What is the value of sin α + cos β, when the values of angle α and β are respectively 30° and 60°?
(a) 1
(b) \frac{1}{2}
(c) 2
(d) 0
Question.2. Find the value of \frac{\sin^{2}30-\sin 0}{\cos^{2}90-\cos^{2}60} .
(a) 0
(b) –1
(c) 1
(d) \frac{1}{2}
Question.3. If α = 90° and β = 60°, determine the value of \sin^{2}α+\cos^{2}β .
(a) \frac{4}{5}
(b) \frac{3}{5}
(c) \frac{5}{4}
(d) \frac{5}{3}
Question.4. If both α and β = 60°, find the value of \sin^{2}α+\cos^{2}β .
(a) 1
(b) 2
(c) –1
(d) –2
Question.5. If in the triangle ABC the lengths of sides AC and BC are in the ratio of 13 : 5, find the value of cosec β.
(a) \frac{5}{13}
(b) \frac{13}{8}
(c) \frac{8}{13}
(d) \frac{13}{5}
Ans.1. (a)
We have a = 30° and that of b = 60°
Thus, sin α + cos β = sin 30° + cos 60° = \frac{1}{2} + \frac{1}{2} = 1.
Ans.2. (b) –1
\frac{\sin^{2}30-\sin 0}{\cos^{2}90-\cos^{2}60} = \frac{(\frac{1}{2})^{2}-0}{0-(\frac{1}{2})^{2}} = \frac{(\frac{1}{4})}{-(\frac{1}{4})} = – 1
Ans.3. (c)
Here, \sin^{2}α+\cos^{2}β = \sin^{2}90°+\cos^{2}60° = (1)^{2}+(\frac{1}{2})^{2} = 1+\frac{1}{4} = \frac{5}{4}
Ans.4. (a) 1
Here, \sin^{2}α+\cos^{2}β = \sin^{2}60°+\cos^{2}60° = (\frac{\sqrt{3}}{2})^{2}+(\frac{1}{2})^{2} = \frac{3}{4}+\frac{1}{4} = 1
Ans.5. (d) 13/5
From the table we can find that cosec β = \frac{AC}{BC} = \frac{13k}{5k} = \frac{13}{5}
Type 2: Theory type
Case Study Question 14
Read the following and answer the questions given below:
Three friends Nikita, Palak and Kanika are playing hide and seek in a park. Nikita, Palak hide in the shrubs and Kanika have to find both of them. If the positions of three friends are at A, B and C respectively as shown in the figure and forms a right angled triangle such that AB = 9 cm, BC = 3\sqrt{3} m and ∠B = 90°, then answer the following question:
Question.1. Find the measure of \angle A and \angle C.
Question.2. What is the distance between Nikita and Kanika?
Ans.1. We have AB = 9 m, BC = 3\sqrt{3} m
In ∆ABC, we have
tan A = \frac{BC}{AB} = \frac{3\sqrt{3}}{9} = \frac{1}{\sqrt{3}}
⇒ tan A = tan 30°
⇒ \angle A = 30°
Similarly, tan C = \frac{AB}{BC} = \frac{9}{3\sqrt{3}} = \sqrt{3}
⇒ tan C = tan 60°
⇒ \angle C = 60°.
Ans.2. Since sin A = \frac{BC}{AC}
⇒ sin 30° = \frac{3\sqrt{3}}{AC}
⇒ \frac{1}{2} = \frac{3\sqrt{3}}{AC}
⇒ AC = 6\sqrt{3} m
Hence, the distance between Nikita and Kanika is 6\sqrt{3} m.