Hint: Discuss the different tools of construction in order to describe their uses.
Question.1. Which pair of angles can be drawn using set-squares?
(a) 15° and 30°
(b) 15° and 45°
(c) 30° and 45°
(d) 45° and 50°
Question.2. A teacher asked his students to enlist the minimum tools required to draw a square inscribed in a circle.
The responses of two of the students are as shown.
Student 1: Ruler and compasses
Student 2: Set-square and compasses
Who among them is/are correct?
(a) Only Student 1
(b) Only Student 2
(c) Both Student 1 and Student 2
(d) Neither Student 1 nor Student 2
Ans.1. (c) 30° and 45°
Ans.2. (c) Both Student 1 and Student 2
Hint: List and execute steps of construction in order to construct a circle when its radius is known.
Question.3. Rohit has to construct a circle of radius 4.8 cm. Which of the following steps should he follow?
(a)
Step 1: Open the compasses for 2.4 cm.
Step 2: Mark a point with a pencil as the centre of the circle. Name it as C.
Step 3: Place the pointer of the compasses on C.
Step 4: Turn the compasses to draw the circle.
(b)
Step 1: Draw a line segment \overline{AB} of length 4.8 cm.
Step 2: Open the compasses for 4.8 cm.
Step 3: Place the pointer at the mid-point, say C, of the line segment \overline{AB}.
Step 4: Turn the compasses to draw the circle.
(c)
Step 1: Open the compasses for 4.8 cm.
Step 2: Mark a point with a pencil as the centre of the circle. Name it as C.
Step 3: Place the pointer of the compasses on C.
Step 4: Turn the compasses to draw the circle.
(d)
Step 1: Draw a line segment \overline{AB} of length 2.4 cm.
Step 2: Open the compasses for 2.4 cm.
Step 3: Place the pointer at A.
Step 4: Turn the compasses to draw the circle.
Question.4. To draw a circle of radius 6 cm, Anjali writes the following steps.
Step 1: Draw a line segment \overline{EF} of 6 cm.
Step 2: Mark the mid-point of the line segment, say G.
Step 3: Taking G as the centre and GF as the arc, draw the required circle.
Are her steps for the required construction correct?
(a) Yes, because EF = 2GF
(b) No, because the centre of the circle should lie in between G and F.
(c) Yes, because EF is the radius of the circle and its length is 6 cm.
(d) No, because the centre of the circle should either be E or F.
Ans.3. (c)
Step 1: Open the compasses for 4.8 cm.
Step 2: Mark a point with a pencil as the centre of the circle. Name it as C.
Step 3: Place the pointer of the compasses on C.
Step 4: Turn the compasses to draw the circle.
Ans.4. (d) No, because the centre of the circle should either be E or F.
Hint: List and execute steps of construction in order to construct a line segment when its length is known.
Question.5. Kunal wrote the following steps to construct a line segment of 7 cm.
Step 1: Draw a line k. Mark a point M on the line k.
Step 2: Place the compasses pointer on the mark “1” of the ruler.
Step 3: Open the compasses to place the pencil point up to the mark “7” of the ruler.
Step 4: Taking caution that the opening of the compasses has not changed, place the pointer on M and draw an arc to cut k at N to get \overline{MN} = 7 cm.
Kunal made an error while constructing the line segment. In which step did he make the error?
(a) Step 1
(b) Step 2
(c) Step 3
(d) Step 4
Question.6. Estimate the length of QR based on the given construction.
Step 1: Draw a line segment \overline{MN} = 10.4 cm.
Step 2: Draw another line segment \overline{OP} = 4.5 cm .
Step 3: Adjust the compasses up to the length of \overline{OP} and put the pointer of compasses at M to draw an arc intersecting \overline{MN} at K.
Step 4: Draw a line l and mark a point Q on it.
Step 5: Adjust the compasses up to the length \overline{KN} and put the pointer of compasses at Q to draw an arc intersecting the line l at R.
(a) 4.5 cm
(b) 5.9 cm
(c) 6.9 cm
(d) 14.9 cm
Ans.5. (b) Step 2
Ans.6. (b) 5.9 cm
Hint: List and execute steps of construction in order to construct a copy of the given line segment.
Question.7. A line segment \overline{PQ} is shown.Which of these options shows the correct steps to construct a copy of the line segment \overline{PQ}?
(a)
Step 1: Fix the compasses pointer at the mid-point of \overline{PQ}, say T, and the pencil end on Q.
Step 2: Draw any line m. Choose a point U on m. Without changing the compasses setting, place the pointer on U.
Step 3: Draw an arc that cuts m at a point, say V. Now \overline{UV} is the required line segment.
(b)
Step 1: Fix the compasses pointer on P and the pencil end on Q.
Step 2: Draw any line m. Choose a point U on m. Without changing the compasses setting, place the pointer on U.
Step 3: Draw an arc that cuts m at a point, say V. Now \overline{UV} is the required line segment.
(c)
Step 1: Fix the compasses pointer at the mid-point of \overline{PQ}, say T, and the pencil end on P.
Step 2: Draw any line m. Choose a point U on m. Without changing the compasses setting, place the pointer on U.
Step 3: Draw an arc that cuts m at a point, say Y.
Step 4: Fix the compasses pointer at the mid-point of \overline{UV}, say S, draw an arc that cuts m at a point, say V. Now \overline{UV} is the required line segment.
(d)
Step 1: Fix the compasses pointer on P and the pencil end on Q.
Step 2: Draw any line m. Choose a point U on m. Without changing the compasses setting, place the pointer on U.
Step 3: Draw an arc that cuts m at a point, say Y.
Step 4: Without changing the compasses setting, place the pointer on Y and draw an arc that cuts m at a point, say V. Now \overline{UV} is the required line segment.
Question.8. Richa constructs a line segment by following the given steps.
Step 1: Draw a line segment \overline{EF}.
Step 2: Draw a line l and mark a point G on it.
Step 3: Adjust the compasses up to the length of \overline{EF} and put the pointer of compasses at G to draw an arc intersecting the line l at H.
Step 4: Without changing the compasses setting and H as centre, draw an arc intersecting the line l at J.
Based on the information, which relation holds true?
(a) \overline{EF} = 2\overline{GH}
(b) \overline{GH} = 2\overline{GJ}
(c) 2\overline{EF} = \overline{GJ}
(d) 2\overline{GH} = \overline{HJ}
Ans.7. (b)
Step 1: Fix the compasses pointer on P and the pencil end on Q.
Step 2: Draw any line m. Choose a point U on m. Without changing the compasses setting, place the pointer on U.
Step 3: Draw an arc that cuts m at a point, say V. Now \overline{UV} is the required line segment.
Ans.8. (c) 2\overline{EF} = \overline{GJ}
Hint: List and execute steps of construction in order to construct a perpendicular to a line through a point on it.
Question.9. A teacher gave a construction problem. Aarav followed the given steps for construction.
Step 1: Draw a line u.
Step 2: Mark point S on line u.
Step 3: Place a ruler with one of its edges along u.
Step 4: Place a set-square with one of its edges along the already aligned edge of the ruler such that the right-angled corner is in contact with the ruler.
Step 5: Slide the set-square along the edge of ruler until its right-angled corner coincides with S.
Step 6: Draw ST along the edge of the set-square.
What problem was given by the teacher for construction?
(a) To construct an acute angle to a line through a point on it.
(b) To construct a perpendicular to a line through a point on it.
(c) To construct an obtuse angle to a line through a point on it.
(d) To construct a perpendicular to a line through a point not on it.
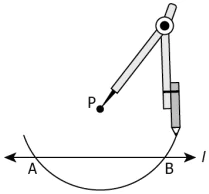
Question.10. Rishabh writes the following steps to construct a perpendicular to a line through a point on it.
Step 1: Draw a line l and mark a point P on it.
Step 2: With P as the centre and a convenient radius, draw an arc intersecting the line l at two points A and B.
Step 3: With A as the centre and radius equal to AP, draw an arc.
Step 4: With B as the centre and radius equal to BP, draw an arc intersecting the arc drawn in Step 3 at Q.
Step 5: Join PQ. Then \overleftrightarrow{PQ} is perpendicular to l.
Is his construction correct?
(a) Yes, because the length of AP is equal to the length of BP.
(b) No, because the radius used in Step 3 should be less than AP and the same radius should be used in Step 4.
(c) Yes, because P and Q lie on a single straight line.
(d) No, because the radius used in Step 3 should be greater than AP and the same radius should be used in Step 4.
Ans.9. (b) To construct a perpendicular to a line through a point on it.
Ans.10. (d) No, because the radius used in Step 3 should be greater than AP and the same radius should be used in Step 4.
Hint: List down and execute steps of construction in order to construct a perpendicular to a line through a point not on it.
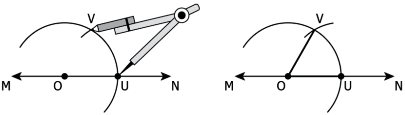
Question.11. The steps to construct a perpendicular to a line w through a point which does not lie on the line w are shown below.
Step 1: Mark point K outside the line w.
Step 2: Place a ruler along the edge opposite to the right angle of the set-square.
Step 3: Place a set-square on w such that one arm of its right angle aligns along w.
Step 4: Hold the ruler fixed. Slide the set-square along the ruler till the point K touches the other arm of the set-square.
Step 5: Join KL along the edge through K, meeting w at L.
Which two steps should be swapped so that the construction becomes possible?
(a) Step 2 and Step 4
(b) Step 3 and Step 4
(c) Step 2 and Step 3
(d) Step 3 and step 5
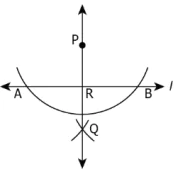
Question.12. The correct steps to construct a perpendicular to a line through a point not on it are as shown.
Step 1: 
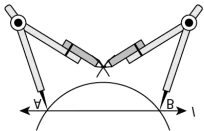
Which of these conditions is sufficient to justify the construction?
(a) \overline{PA} = \overline{PB}
(b) \overline{PA} = \overline{PB} = \overline{BQ}
(c) \overline{PA} = \overline{PB} = \overline{BQ} = \overline{AQ}
(d) \overline{PA} = \overline{PB} = \overline{BQ} = \overline{AQ} = \overline{PR}
Ans.11. (c) Step 2 and Step 3
Ans.12. (c) \overline{PA} = \overline{PB} = \overline{BQ} = \overline{AQ}
Hint: Use a protractor and ruler in order to construct an angle of the given measure.
Question.13. Consider the line segment.Which of these options correctly shows the complete steps to construct an angle of measure 50° using protractor?
(a) 


Question.14. A teacher asks her students to join the alphabets such that the resulting angle is 30°.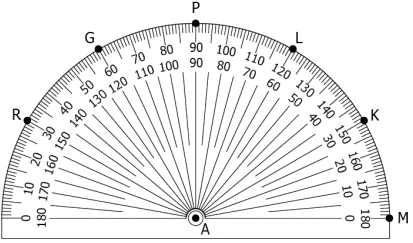
Ujjwal: Joins AR and AM
Satyam: Joins AM and AK
Abhishek: Joins AP and AL
Virendra: Joins AP and AG
How many of them responded correctly?
(a) None
(b) Only one student
(c) Only two students
(d) Only three students
Ans.13. (b) 
Hint: List and execute steps of construction in order to construct a copy of the given angle of unknown measure using a compass.
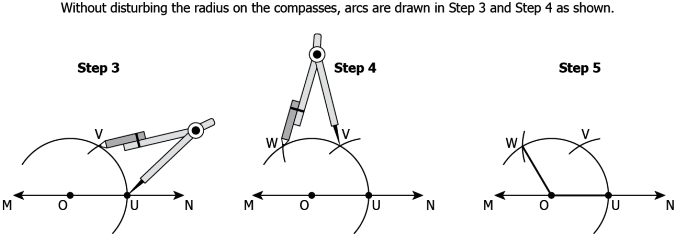
Question.15. A teacher draws \angle AOB as shown and asks his students to write the steps in order to construct the copy of the given angle.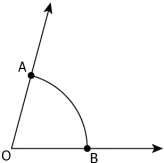
Student 1:
- Step 1: Draw a line l and mark a point P on it.
- Step 2: Place the compasses at O and set the compass to length OA.
- Step 3: Using the same compasses setting and with P as centre, draw an arc cutting l in Q.
- Step 4: Set the compasses to the length AB and with Q as centre, draw an arc intersecting the arc drawn in Step 3 at R.
- Step 5: Join PR to get \angle O = \angle P.
Student 2:
- Step 1: Draw a line l and mark a point P on it.
- Step 2: Place the compasses at A and set the compass to length AB.
- Step 3: Using the same compasses setting and with P as centre, draw an arc cutting l in Q.
- Step 4: Set the compasses to the length OB and with Q as centre, draw an arc intersecting the arc drawn in Step 3 at R.
- Step 5: Join PR to get \angle O = \angle P.
Who among them is/are correct?
(a) Only Student 1
(b) Only Student 2
(c) Both Student 1 and Student 2
(d) Neither Student 1 nor Student 2
Question.16. Consider \angle A as shown.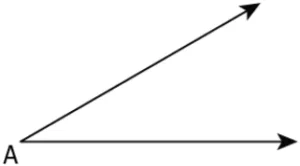
- Step 1: Draw a line l and mark a point M on it.
- Step 2: Place the compasses at A and draw an arc to cut the rays of \angle A at B and C.
- Step 3: Using the same radius used in Step 2 and with M as centre, draw an arc cutting l in N.
- Step 4: Taking radius equal to AB and N as the centre, draw an arc intersecting the arc drawn in Step 3 at P.
- Step 5: Join M to P to get \angle A = \angle M.
In which step did the student make the first error and what should be the correct step?
(a) Step 3: Using the smaller radius than that of used in Step 2 and with M as centre, draw an arc cutting l in N.
(b) Step 3: Using the greater radius than that of used in Step 2 and with M as centre, draw an arc cutting l in N.
(c) Step 4: Taking radius equal to BC and N as the centre, draw an arc intersecting the arc drawn in Step 3 at P.
(d) Step 4: Taking radius equal to AC and N as the centre, draw an arc intersecting the arc drawn in Step 3 at P.
Ans.15. (a) Only Student 1
Ans.16. (c) Step 4: Taking radius equal to BC and N as the centre, draw an arc intersecting the arc drawn in Step 3 at P.
Hint: List and execute steps of construction in order to construct the bisector of an angle and construct angles of measures 30°, 45° and so on.
Question.17. Part of construction of an angle measuring 45° is shown below.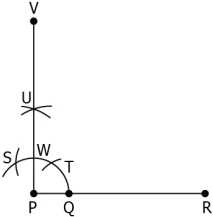
(a)
Step 1: Taking the radius greater than \frac{WQ}{2} and with centres P and Q, draw two arcs which cut each other at a point X.
Step 2: Join PX to get \angle RPX = 45°.
(b)
Step 1: Taking the radius less than \frac{WQ}{2} and with centres P and Q, draw two arcs which cut each other at a point X.
Step 2: Join PX to get \angle RPX = 45°.
(c)
Step 1: Taking the radius greater than \frac{WQ}{2} and with centres W and Q, draw two arc which cuts each other at a point X.
Step 2: Join PX to get \angle RPX = 45°.
(d)
Step 1: Taking the radius less than \frac{WQ}{2} and with centres W and Q, draw two arcs which cuts each other at a point X.
Step 2: Join PX to get \angle RPX = 45°.
Question.18. Consider an angle shown below.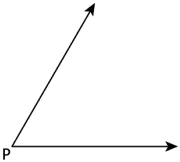
Step 1: With P as centre and a convenient radius, draw an arc that cuts both rays of \angle P. Label the points of intersection as Q and R.
Step 2: With Q as centre, draw (in the interior of \angle P) an arc with radius greater than half the length QR.
Step 3: With twice the radius used in Step 2 and with R as centre, draw another arc in the interior of \angle P.
Let the two arcs intersect at S. Then PS is the required bisector of \angle P.
Which step in the given construction is incorrect and what should be the correct step?
(a) Step 2: With Q as centre, draw (in the interior of \angle P) an arc whose radius is smaller than half the length \overline{QR}.
(b) Step 3: With the same radius as used in Step 2 and with R as centre, draw another arc in the interior of \angle P. Let the two arcs intersect at S. Then \overline{PS} is the required bisector of \angle P.
(c) Step 2: With Q as centre, draw (in the interior of \angle P) an arc whose radius is equal to the length \overline{QR}.
(d) Step 3: With the smaller radius than that used in Step 2 and with R as centre, draw another arc in the interior of \angle P. Let the two arcs intersect at S. Then \overline{PS} is the required bisector of \angle P.
Ans.17. (c)
Step 1: Taking the radius greater than \frac{WQ}{2} and with centres W and Q, draw two arc which cuts each other at a point X.
Step 2: Join PX to get \angle RPX = 45°.
Ans.18. (b)
Step 3: With the same radius as used in Step 2 and with R as centre, draw another arc in the interior of \angle P. Let the two arcs intersect at S. Then \overline{PS} is the required bisector of \angle P.
Hint: List and execute steps of construction in order to construct angles of measures 60°, 90° and 120°.
Question.19. The first two steps to construct an angle of measure 120° are as shown.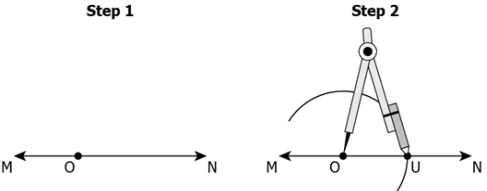
(a) 
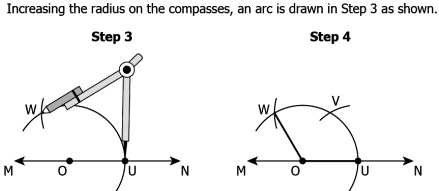
Question.20. A student wrote the following steps to construct an angle of measure 90°.
- Step 1: Draw a line segment \overline{OB}.
- Step 2: With O as centre, draw an arc intersecting \overline{OB} at P.
- Step 3: Taking the radius greater than that of used in Step 2 and with P as the centre, draw an arc intersecting the arc drawn in Step 2 at D.
- Step 4: Taking the radius greater than that of used in Step 3 and with D as the centre, draw an arc intersecting the arc drawn in Step 2 at E.
- Step 5: Taking the same radius used in Step 4 and with D and E as centres, draw two arcs intersecting each other at a point, say F.
- Step 6: Join OF to form \angle BOF = 90°.
In which step did the student make the first error and what should be the correct step?
(a) Step 3: Taking the same radius used in Step 2 and with P as the centre, draw an arc intersecting the arc drawn in Step 2 at D.
(b) Step 3: Taking the radius smaller than that of used in Step 2 and with P as the centre, draw an arc intersecting the arc drawn in Step 2 at D.
(c) Step 4: Taking the same radius used in Step 3 and with D as the centre, draw an arc intersecting the arc drawn in Step 2 at E.
(d) Step 4: Taking the smaller than that of used in Step 3 and with D as the centre, draw an arc intersecting the arc drawn in Step 2 at E.
Ans.19. (c)