Hint: Calculate area of a given triangle to state the limitation of the Standard formula (Area of Triangle = \frac{1}{2}\times b \times h).
Question.1. Two triangles are shown below.
(a) Area of both the triangles can be calculated, area of ∆XYZ = 140 cm^{2} and area of ∆PQR = 180 cm^{2}
(b) Area of only triangle XYZ can be calculated, area of ∆XYZ = 140 cm^{2}
(c) Area of only triangle PQR can be calculated, area of ∆PQR = 180 cm^{2}
(d) Area of both the triangles cannot be calculated
Question.2. A figure is shown below.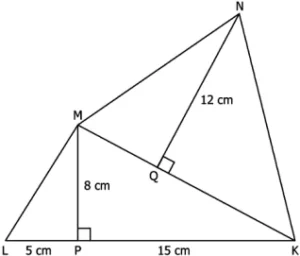
(a) No, as the side MK is unknown.
(b) No, as the side NK is unknown.
(c) Yes, and the area of the quadrilateral KLMN is 192 cm^{2}.
(d) Yes, and the area of the quadrilateral KLMN is 384 cm^{2}.
Ans.1. (c) Area of only triangle PQR can be calculated, area of ∆PQR = 180 cm^{2}
Ans.2. (c) Yes, and the area of the quadrilateral KLMN is 192 cm^{2}.
Hint: Apply Heron’s formula in order to calculate the area of a Triangle.
Question.3. A triangle is shown below.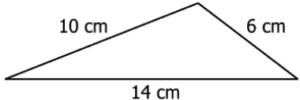
(a) \sqrt{(9)(5)(1)}
(b) \sqrt{15(9)(5)(1)}
(c) \sqrt{(24)(20)(16)}
(d) \sqrt{30(24)(20)(16)}
Question.4. A triangle is shown below.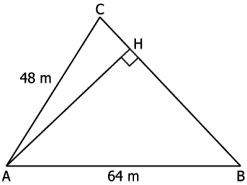
(a) 38.4 m
(b) 40 m
(c) 76.8 m
(d) 80 m
Ans.3. (b) \sqrt{15(9)(5)(1)}
Ans.4. (a) 38.4 m
Hint: Breakdown a given polygon into triangles in order to find the area of a given polygon as a sum of areas of those triangles.
Question.5. A quadrilateral ABCD is shown below.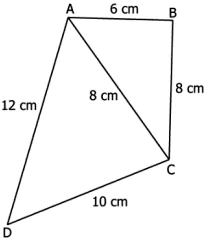
(a) 61.94 cm^{2}
(b) 86.96 cm^{2}
(c) 123.88 cm^{2}
(d) 173.92 cm^{2}
Question.6. The sketch of a farm is shown below.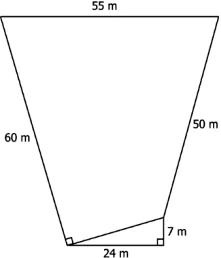
(a) 1336.04 m^{2}
(b) 2140.04 m^{2}
(c) 2170.04 m^{2}
(d) 3004.04 m^{2}
Ans.5. (a) 61.94 cm^{2}
Ans.6. (c) 2170.04 m^{2}




