Hint: Visualize a cube and cuboid in its 2-D form in order to calculate the surface area.
Question.1. The 2-D representation of a figure is given below: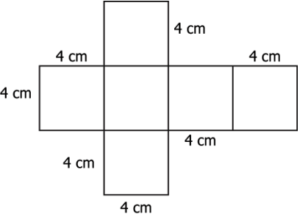
(a) 4^{2} cm^{2}
(b) 4^{2}+4^{2}+4^{2}+4^{2} cm^{2}
(c) 4^{2}+4^{2}+4^{2}+4^{2}+4^{2} cm^{2}
(d) 4^{2}+4^{2}+4^{2}+4^{2}+4^{2}+4^{2} cm^{2}
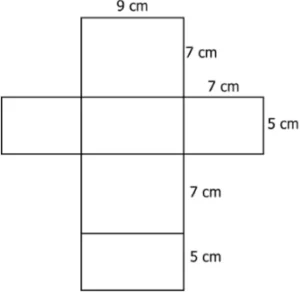
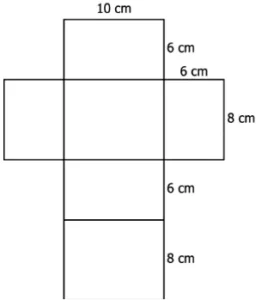
Question.2. Which of these is a 2-D representation of the cuboid whose total surface area is 510 cm^{2}?
(a) 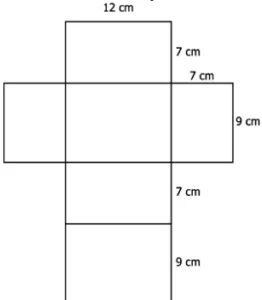
Ans.1. (d) 4^{2}+4^{2}+4^{2}+4^{2}+4^{2}+4^{2} cm^{2}
Ans.2. (a)
Hint: Calculate the surface area (lateral and total) of the cube or cuboid in order to determine the cost of painting/covering the given surface.
Question.3. Ajay needs to cover 15 cube shaped boxes each of side length 10 cm using a paper. If 1 cm^{2} of paper costs him ₹0.25, what is the total cost of covering 15 boxes?
(a) ₹1,125
(b) ₹1,500
(c) ₹2,250
(d) ₹3,750
Question.4. Rajeev is painting 18 identical boxes. He paints the top and bottom with red colour and the remaining four faces with blue colour. He paints a total of 3.1680 m^{2} area with blue color. If each box is 32 cm long and 22 cm deep, what is the breadth of each box?
(a) 3.25 cm
(b) 8 cm
(c) 22.5 cm
(d) 45 cm
Ans.3. (c) ₹2,250
Ans.4. (b) 8 cm
Hint: Visualize a cylinder in its 2-D form in order to calculate the curved surface area and total surface area.
Question.5. Consider the 2-D representation of a solid below: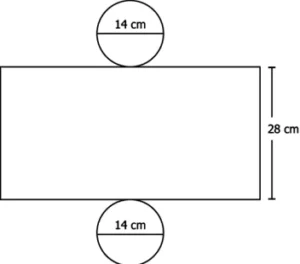
(a) 2 × π × 14 × 28 = 2,464 cm^{2}
(b) 2 × π × 7 × 28 = 1,232 cm^{2}
(c) 2 × π × 14(14 + 28) = 3,696 cm^{2}
(d) 2 × π × 7(7 + 28) = 1,540 cm^{2}
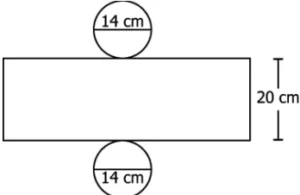
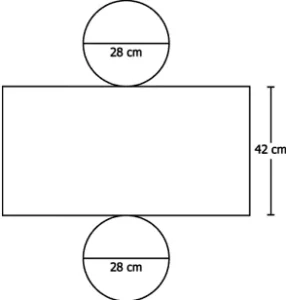
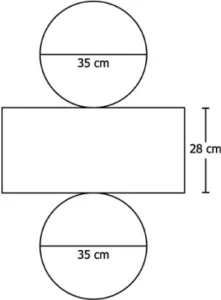
Question.6. Which of these represents the net of a cylinder whose lateral surface area is 880 cm2 and total surface area is 1,188 cm^{2}? (Use \frac{22}{7} for π)
(a) 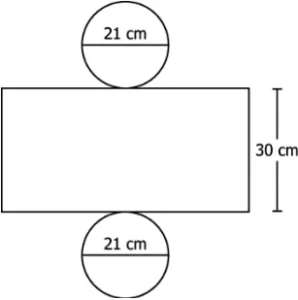
Ans.5. (b) 2 × π × 7 × 28 = 1,232 cm^{2}
Ans.6. (d)
Hint: Calculate the surface area (curved and total) of a cylinder to determine the cost of painting/covering the given surface.
Question.7. Jatin made a model in the shape of a cylinder of radius 7 cm and height 14 cm for his school project. He wants to use colored sheet to decorate the model except the top and bottom. If the coloured sheet costs ₹0.75 per cm^{2}, what will be the total cost to decorate the model? (Use \frac{22}{7} for π)
(a) ₹462
(b) ₹693
(c) ₹924
(d) ₹1,617
Question.8. A factory manufactures cylindrical storage tanks made of steel who’s top and bottom ends are closed in batches. The curved surface area and height of each tank is 22000 cm^{2} and 100 cm respectively. If each batch contains a dozen of storage tanks and the cost of steel sheets used in manufacturing is ₹18 per square centimeter, how much would it cost to manufacture a batch?
(a) ₹ 3,56,400
(b) ₹ 5,34,600
(c) ₹ 47,52,000
(d) ₹ 64,15,200
Ans.7. (a) ₹462
Ans.8. (d) ₹ 64,15,200
Hint: Visualize a right circular cone in 2-D in order to calculate the surface area (curved and total).
Question.9. The 2-D representation of a figure is given below.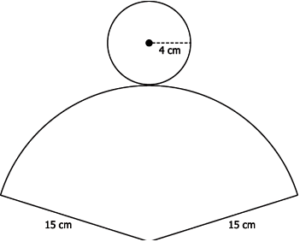
(a) π × 4 cm × 15 cm
(b) π × (4 cm + 15 cm)
(c) π × 4 cm × (4 cm + 15 cm)
(d) 2 × π × 4 cm × (4 cm + 15 cm)
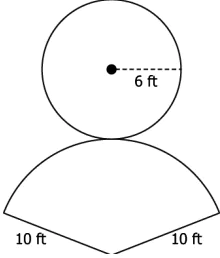
Question.10. Which of these represents the correct net of the right circular cone whose total surface area is 301.44 feet^{2}?
(a) 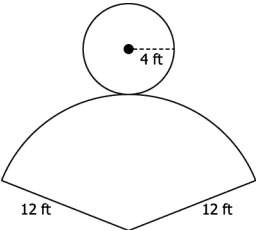
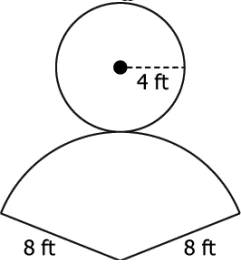
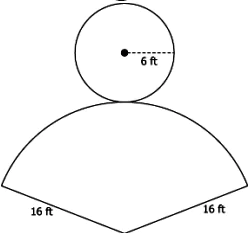
Ans.9. (a) π × 4 cm × 15 cm
Ans.10. (d)
Hint: Calculate the surface area (curved and total) of a cone to determine the cost of painting/covering the given surface.
Question.11. A heap of wheat is in the form of a cone whose diameter is 4.2 m and height is 2.8 m. The heap is to be covered exactly by a canvas to protect it from rain. If the rate of the canvas is ₹3 per m^{2}, what is the total cost of the canvas needed to cover the heap?
(a) ₹69.3
(b) ₹82.53
(c) ₹144.3
(d) ₹201.96
Question.12. Asif is building a birdhouse. The roof of the birdhouse is in the form of a right circular cone whose radius is 21 cm and slant height is 47 cm. He plans to paint the roof red, but he needs to know the surface area to buy the right amount of paint. What is the surface area of the roof, including the bottom?
(a) 3231.06
(b) 3321.06
(c) 3123.06.
(d) 3132.06
Ans.11. (a) ₹69.3
Ans.12. (a) 3231.06
Hint: Calculate the surface area of a sphere/hemisphere to determine the cost of painting/covering the given surface of a sphere/hemisphere.
Question.13. A hemispherical bowl made of brass has inner radius 5.25 cm. What is the total cost of tin-plating it on the inside at the rate of ₹4 per cm^{2}?
(a) ₹6.93
(b) ₹69.3
(c) ₹693
(d) ₹6930
Question.14. A hemispherical dome of a tomb needs to be painted. The circumference of the base of the dome is 17.6 cm. If the cost of painting is ₹7 per cm^{2}, what is the cost, rounded to the nearest rupee, to paint the dome? (Use \frac{22}{7} for π)
(a) ₹345
(b) ₹390
(c) ₹571
(d) ₹690
Ans.13. (c) ₹693
Ans.14. (a) ₹345
Hint: Calculate the volume of a given cube in order to infer the quantity of any substance it can hold.
Question.15. A milk tank is in the form of cube whose edge length is 8 m. How much quantity of milk, in cubic metres, can be stored in the tank?
(a) 64
(b) 384
(c) 512
(d) 800
Question.16. The capacity of a warehouse is usually measured by 12 m × 12 m × 12 m. What is the maximum number of cartons each measuring 0.75 m × 0.75 m × 0.75 m that can be stored in the warehouse?
(a) 512
(b) 987
(c) 1727
(d) 4096
Ans.15. (c) 512
Ans.16. (d) 4096
Hint: Calculate the volume of a given cuboid in order to infer the quantity of any substance it can hold.
Question.17. A tank in the shape of cuboid is 45 cm long, 25 cm wide and 35 cm deep. What is the capacity, in cubic centimeters, of the tank?
(a) 102
(b) 3,575
(c) 5,150
(d) 39,375
Question.18. Abhinav stored 1,750 cuboidal cartons each measuring 30 cm × 45 cm × 20 cm in a hall, which is completely filled. The hall is 4.5 m long and 3.5 m wide, what is the height of the hall?
(a) 300 cm
(b) 200 cm
(c) 160 cm
(d) 100 cm
Ans.17. (d) 39,375
Ans.18. (a) 300 cm
Hint: Calculate the volume of a given cylinder in order to infer the quantity of any substance it can hold.
Question.19. A cylindrical water storage tank has an inside base radius of 7 m and depth of 11 m. How many cubic centimeters of water can it hold? (Use \frac{22}{7} for π)
(a) 3388 m^{3}
(b) 1694 m^{3}
(c) 847 m^{3}
(d) 484 m^{3}
Question.20. After painting his car parking, Ravi has \frac{1}{5} of a cylindrical can of paint remaining. The can has a radius of 15 cm and a height 30 cm. He wants to pour the remaining paint into a smaller can for storage. The smaller can has a radius of 10 cm. What should be the minimum height of the smaller can in order to hold all of the paint?
(a) 67.5 cm
(b) 45 cm
(c) 13.5 cm
(d) 4:9 cm
Ans.19. (b) 1694 m^{3}
Ans.20. (c) 13.5 cm
Hint: Calculate the volume of a given cone in order to infer the quantity of any substance it can hold.
Question.21. How many cubic centimeters of water can a conical vessel of base diameter 42 cm and slant height 29 cm hold?
(a) 1,914 cm^{3}
(b) 9,240 cm^{3}
(c) 13,398 cm^{3}
(d) 36,960 cm^{3}
Question.22. The radius and height of a conical cup is in the ratio 3:4. If the volume of the cup is 2,376 cm^{3}, which of these can be slant height of the cone, rounded off to the nearest whole number?
(a) 3 cm
(b) 4 cm
(c) 15 cm
(d) 20 cm
Ans.21. (b) 9,240 cm^{3}
Ans.22. (d) 20 cm
Hint: Calculate the volume of a given sphere in order to infer the quantity of any substance it can hold.
Question.23. What is the volume, rounded to the nearest whole number, of metallic spherical ball of radius 4.5 cm? (Use \frac{22}{7} for π)
(a) 19 cm^{3}
(b) 38 cm^{3}
(c) 156 cm^{3}
(d) 382 cm^{3}
Question.24. There are 15 metallic solid identical spherical objects to be loaded on trucks. The diameter of the object is 80 cm. The density of the metal is 7 g/cm^{3}. Each truck can carry the maximum load of 6000 kg, what is the greatest number of objects that can be loaded on a truck? (Use \frac{22}{7} for π)
(a) 3
(b) 4
(c) 5
(d) 6
Ans.23. (d) 382 cm^{3}
Ans.24. (b) 4
Hint: Calculate the volume of a given hemisphere in order to infer the quantity of any substance it can hold.
Question.25. A hemispherical bowl of diameter 21 cm is completely filled with milk. How many litres of milk, to the nearest tenth, is contained in the bowl? (Use \frac{22}{7} for π)
(a) 0.2
(b) 1.4
(c) 2.4
(d) 4.9
Question.26. Fifteen metallic hemispheres of radius 4.5 cm are melted to form 3 identical big hemispheres. If the density of the metal is 8.5 g/cm^{3}, what is the mass of a bigger hemisphere? (Use \frac{22}{7} for π)
(a) 965 g
(b) 8130.63 g
(c) 8138.75 g
(d) 16,261.35 g
Ans.25. (c) 2.4
Ans.26. (b) 8130.63 g