NCERT Solutions Class 10 Maths Chapter 2 Polynomials
NCERT Solutions
Exercise 2.1
Question.1. The graphs of y = p(x) are given in fig. below, for some polynomials p(x). Find the number of zeroes of p(x), in each case.
(i) 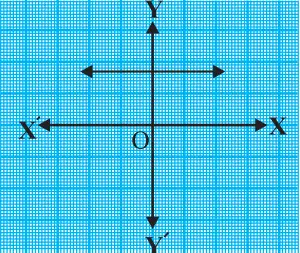
(ii) 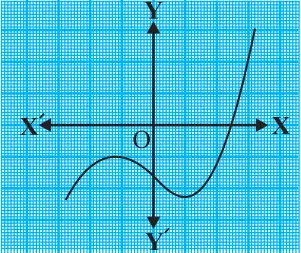
(iii) 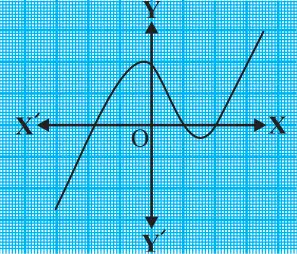
(iv) 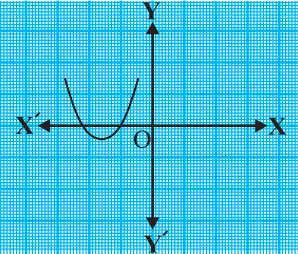
(v) 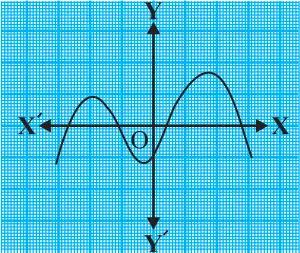
(vi) 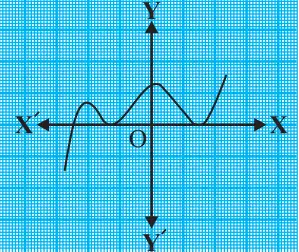
Exercise 2.2
Question.1. Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients :
(i) x^{2}-2x-8
Solution: Let p(x) = x^{2}-2x-8
= x^{2}-4x+2x-8
= x(x-4)+2(x-4)
= (x – 4)(x + 2)
For finding the zeroes
Put, p(x) = 0
= (x – 4)(x + 2) = 0
x = 4, – 2
Verification: Now, sum of zeroes = 4 + (– 2)
= {\frac{2}{1}}
= {\frac{-(Coefficient of x)}{(Coefficient of x^{2})}}
Product of zeroes = 4 \times (– 2)
= {\frac{-8}{1}}
= {\frac{Constant term}{Coefficient of x^{2}}}
Hence, relationship between the zeroes and the coefficients is true.
(ii) 4s^{2}-4s+1
Solution: Let p(s) = 4s^{2}-4s+1
= 4s^{2}-2s-2s+1
= 2s(2s-1)-1(2s-1)
= (2s – 1) (2s – 1)
= (2s-1)^{2}
For finding the zeroes, put p(s) = 0.
2s – 1 = 0
s = \frac{1}{2}
Hence, zeroes of p(s) are \frac{1}{2} and 12 \frac{1}{2} .
Verification: Now, sum of zeroes = \frac{1}{2} + \frac{1}{2}
= 1 = \frac{4}{4} = {\frac{-(Coefficient of s)}{(Coefficient of s^{2})}}
Product of zeroes = \frac{1}{2} \times \frac{1}{2}
= \frac{1}{4}
= {\frac{Constant term}{Coefficient of s^{2}}}
Hence, relationship between the zeroes and the coefficients is true.
(iii) 6x^{2}-3-7x
Solution: Let p(x) = 6x^{2}-3-7x = 6x^{2}-7x-3
= 6x^{2}-9x+2x-3
= 3x(2x-3)+1(2x-3)
= (2x – 3) (3x + 1)
For finding the zeroes put p(x) = 0
(2x – 3) (3x + 1) = 0
x = {\frac{3}{2}}, {\frac{-1}{3}}
Hence, zeroes of the polynomial are {\frac{3}{2}} and {\frac{-1}{3}}.
Verification: Now sum of zeroes = {\frac{3}{2}} + {\frac{-1}{3}}
= {\frac{9-2}{6}}
= {\frac{7}{6}}
= {\frac{-(Coefficient of x)}{(Coefficient of x^{2})}}
Product of zeroes = {\frac{3}{2}} \times {\frac{(-1)}{3}}
= {\frac{-3}{6}}
= {\frac{Constant term}{Coefficient of x^{2}}}
(iv) 4u^{2}+8u
Solution: Let p(u) = 4u^{2}+8u
= 4u (u + 2)
For finding the zeroes put p(u) = 0,
4u (u + 2) = 0
u = 0, – 2
Hence, zeroes are 0 and – 2.
Verification: Now sum of zeroes = 0 + (– 2)
= {\frac{-2}{1}} \times {\frac{4}{4}}
= {\frac{-8}{4}}
= {\frac{-(Coefficient of u)}{(Coefficient of u^{2})}}
Product of zeroes = 0 \times (– 2)
= {\frac{0}{1}} \times {\frac{4}{4}}
= {\frac{0}{4}}
= {\frac{Constant term}{Coefficient of u^{2}}}
Hence, relationship between the zeroes and the coefficients is true.
(v) t^{2}-15
Solution: Let p(t) = t^{2}-15 .
= t^{2}-(\sqrt{15})^{2}
= (t-\sqrt{15})(t+\sqrt{15}) [∵ a^{2}-b^{2} = (a + b) (a – b)]
For finding the zeroes put p(t) = 0,
(t-\sqrt{15})(t+\sqrt{15}) = 0
t = -\sqrt{15}) , \sqrt{15}
Verification: Sum of the zeroes = -\sqrt{15}) + \sqrt{15}
= {\frac{0}{1}}
= = {\frac{-(Coefficient of t)}{(Coefficient of t^{2})}}
Product of zeroes = -\sqrt{15}) \times \sqrt{15}
= {-\frac{15}{1}}
= {\frac{Constant term}{Coefficient of t^{2}}}
Hence, relationship between the zeroes and the coefficients is true.
(vi) 3x^{2}-x-4
Solution: Let p(x) = 3x^{2}-x-4
= 3x^{2}-4x+3x-4
= x(3x – 4) + 1 (3x – 4)
= (x + 1) (3x – 4)
For finding the zeroes put p(x) = 0,
(x + 1) (3x – 4) = 0
x = -1, {\frac{4}{3}}
Verification: Sum of zeroes = -1 + {\frac{4}{3}}
= {\frac{1}{3}}
= = {\frac{-(Coefficient of x)}{(Coefficient of x^{2})}}
Product of zeroes = -1 \times {\frac{4}{3}}
= {\frac{-4}{3}}
= {\frac{Constant term}{Coefficient of x^{2}}}
Hence, relationship between the zeroes and the coefficients is true.
Question.2. Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively.
(i) {\frac{1}{4}}, – 1
Solution: Let quadratic polynomial is p(x) whose zeroes are α and β.
Given that : α + β = 14 and αβ = – 1
So, required polynomial = k[x^{2} – (α + β)x + αβ]
= k\left[x^{2}-\frac{1}{4}x-1\right]
If k = 4, then 4x^{2}-x-4 .
(ii) \sqrt{2}, {\frac{1}{3}}
Solution: Let quadratic polynomial is ax^{2}+bx+c whose zeroes are α and β.
Given that: α + β = \sqrt{2} and αβ = 13
So, required polynomial = k[x^{2} – (α + β)x + αβ]
= k\left[x^{2}-\sqrt{2}x+{\frac{1}{3}}\right]
If k = 3, then 3x^{2}-3 \sqrt{2}x+1 .
(iii) 0, \sqrt{5}
Solution: Let quadratic polynomial is ax^{2}+bx+c whose zeroes are α and β.
Given that: α + β = 0 and αβ = \sqrt{5}
Hence, required polynomial = k[x^{2} – (α + β)x + αβ]
= k\left[x^{2}-0.x+ \sqrt{5} \right]
= k\left[x^{2}+ \sqrt{5} \right]
If k = 1, then x^{2}+ \sqrt{5} .
(iv) 1, 1
Solution: Let quadratic polynomial is ax^{2}+bx+c whose zeroes are α and β.
Given that : α + β = 1 and αβ = 1
Hence, required polynomial = k[x^{2} – (α + β)x + αβ]
= k\left[x^{2}-x+1 \right]
If k = 1, then x^{2}-x+1 .
(v) {\frac{-1}{4}}, {\frac{1}{4}}
Solution: Let quadratic polynomial is ax^{2}+bx+c whose zeroes are α and β.
Given that: α + β = -{\frac{1}{3}} and αβ = {\frac{1}{3}}
So, required polynomial = k[x^{2} – (α + β)x + αβ]
= k\left[x^{2}+\frac{1}{4}x+\frac{1}{4} \right]
If k = 4, then 4x^{2}+x+1 .
(vi) 4, 1
Solution: Let quadratic polynomial is ax^{2}+bx+c whose zeroes are α and β.
Given that: α + β = 4 and αβ = 1
Hence, required polynomial = k[x^{2} – (α + β)x + αβ]
= k\left[x^{2}-4x+1 \right].



