NCERT Solutions Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables
NCERT Solutions
Exercise 3.1
Question.1. Form the pair of linear equations in the following problems, and find their solutions graphically.
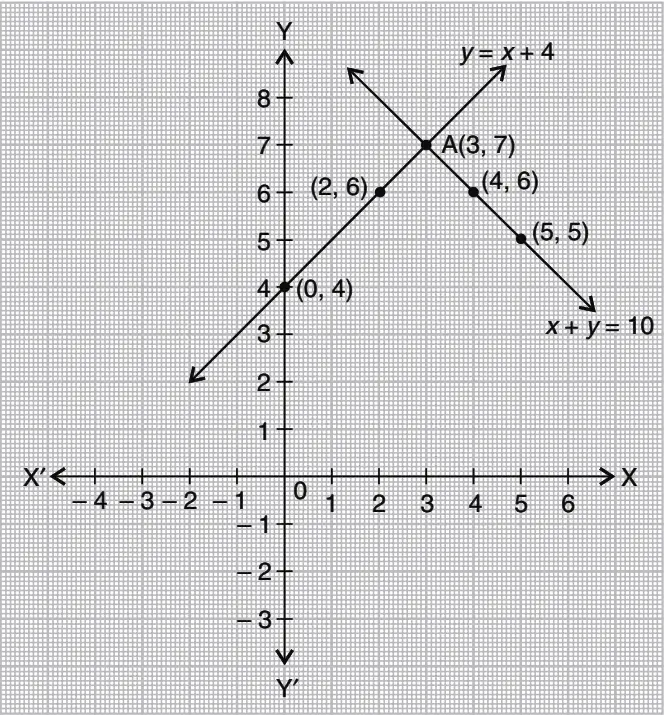
(i) 10 students of Class X took part in a Mathematics quiz. If the number of girls is 4 more than the number of boys, find the number of boys and girls who took part in the quiz.
Solution: Let number of boys = x and number of girls = y
We have, x + y = 10 …(i)
and y = x + 4 …(ii)
Let us find some points of equation (i) to plot on the graph.
x + y = 10
⇒ y = 10 – x ……(iii)
Putting x = 4 in equation (iii), we get
⇒ y = 10 – 4 = 6
Putting x = 3 in equation (iii), we get
⇒ y = 10 – 3 = 7
Putting x = 5 in equation (iii), we get
⇒ y = 10 – 5 = 5
Therefore, Some points on line (i) are:
| x | 4 | 3 | 5 |
| y | 6 | 7 | 5 |
Let us find some points of equation (ii) to plot on the graph.
y = x + 4
Putting x = 0 in equation (ii), we get
⇒ y = 0 + 4 = 4
Putting x = 3 in equation (ii), we get
⇒ y = 3 + 4 = 7
Putting x = 2 in equation (ii), we get
⇒ y = 2 + 4 = 6
Therefore, Some points on line (ii) are:
The two lines meet at A (3, 7), i.e., x = 3, y = 7
Hence, number of boys = 3, number of girls = 7.
| x | 0 | 3 | 2 |
| y | 4 | 7 | 6 |
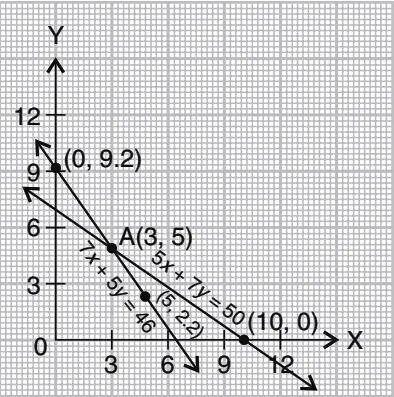
(ii) 5 pencils and 7 pens together cost ₹ 50, whereas 7 pencils and 5 pens together cost ₹ 46. Find the cost of one pencil and that of one pen.
Solution: Let cost of one pencil = ₹ x
and cost of one pen = ₹ y
According to the given condition, we have
5 x + 7 y = 50 …(i)
and 7 x + 5 y = 46 …(ii)
Let us find some points of equation (i) to plot on the graph.
5 x + 7 y = 50
⇒ y = \frac{50-5x}{7} ……(iii)
Putting x = 10 in equation (iii), we get
⇒ y = \frac{50-5 \times 10}{7} = \frac{0}{7} = 0
Putting x = 3 in equation (iii), we get
⇒ y = \frac{50-5 \times 3}{7} = \frac{35}{7} = 5
Putting x = 0 in equation (iii), we get
⇒ y = \frac{50-5 \times 0}{7} = \frac{50}{7} = 7.14
Therefore, Some points on line (i) are:
| x | 10 | 3 | 0 |
| y | 0 | 5 | 7.14 |
Let us find some points of equation (ii) to plot on the graph.
7 x + 5 y = 46
⇒ y = \frac{46-7x}{5} ……(iv)
Putting x = 0 in equation (iv), we get
⇒ y = \frac{46-7 \times 0}{5} = \frac{46}{5} = 9.2
Putting x = 5 in equation (iv), we get
⇒ y = \frac{46-7 \times 5}{5} = \frac{11}{5} = 2.2
Putting x = 3 in equation (iv), we get
⇒ y = \frac{50-7 \times 3}{7} = \frac{29}{7} = 4.14
Therefore, Some points on line (ii) are:
| x | 0 | 5 | 3 |
| y | 9.2 | 2.2 | 4.14 |
Question.2. On comparing the ratios \frac{a_{1}}{a_{2}} , \frac{b_{1}}{b_{2}} and \frac{c_{1}}{c_{2}} , find out whether the lines representing the following pairs of linear equations intersect at a point, are parallel or coincident:
(i) 5 x – 4 y + 8 = 0
7 x + 6 y – 9 = 0
Solution: The given pair of linear equation are :
5 x – 4 y + 8 = 0 …(i)
7 x + 6 y – 9 = 0 …(ii)
Comparing the eqn. (i) and (ii) with a_{1}x + b_{1}y + c_{1} = 0 and a_{2}x + b_{2}y + c_{2} = 0 respectively,
a_{1} = 5, b_{1} = – 4, c_{1} = 8
a_{2} = 7, b_{2} = 6, c_{2} = – 9
Here,
\frac{a_{1}}{a_{2}} = \frac{5}{7}
\frac{b_{1}}{b_{2}} = \frac{-4}{6} = \frac{-2}{3}
\frac{c_{1}}{c_{2}} = \frac{8}{-9}
Clearly, \frac{5}{7} ≠ \frac{-2}{3} ≠ \frac{8}{-9}
Hence, \frac{a_{1}}{a_{2}} ≠ \frac{b_{1}}{b_{2}} ≠ \frac{c_{1}}{c_{2}}
Thus, lines (i) and (ii) intersect at a point, that is, they are intersecting lines.
(ii) 9 x + 3 y + 12 = 0
18 x + 6 y + 24 = 0
Solution: The given pair of linear equation are :
9 x + 3 y + 12 = 0 …(i)
18 x + 6 y + 24 = 0 …(ii)
Comparing the eqn. (i) and (ii) with a_{1}x + b_{1}y + c_{1} = 0 and a_{2}x + b_{2}y + c_{2} = 0 respectively,
a_{1} = 9, b_{1} = 3, c_{1} = 12
a_{2} = 18, b_{2} = 6, c_{2} = 24
Here,
\frac{a_{1}}{a_{2}} = \frac{9}{18} = \frac{1}{2}
\frac{b_{1}}{b_{2}} = \frac{3}{6} = \frac{1}{2}
\frac{c_{1}}{c_{2}} = \frac{12}{24} = \frac{1}{2}
Clearly, \frac{1}{1} = \frac{1}{2} = \frac{1}{2}
Hence, \frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} = \frac{c_{1}}{c_{2}}
Hence, lines (i) and (ii) are coincident lines.
(iii) 6 x – 3 y + 10 = 0
2 x – y + 9 = 0
Solution: The given pair of linear equation are :
6 x – 3 y + 10 = 0 …(i)
2 x – y + 9 = 0 …(ii)
Comparing the eqn. (i) and (ii) with a_{1}x + b_{1}y + c_{1} = 0 and a_{2}x + b_{2}y + c_{2} = 0 respectively,
a_{1} = 6, b_{1} = – 3, c_{1} = 10
a_{2} = 2, b_{2} = – 1, c_{2} = 9
Here,
\frac{a_{1}}{a_{2}} = \frac{6}{2} = \frac{3}{1}
\frac{b_{1}}{b_{2}} = \frac{-3}{-1} = \frac{3}{1}
\frac{c_{1}}{c_{2}} = \frac{10}{9} = = \frac{10}{9}
Clearly, \frac{3}{1} = \frac{3}{1} ≠ \frac{10}{9}
Hence, \frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} ≠ \frac{c_{1}}{c_{2}}
Thus, lines (i) and (ii) are parallel lines.
Question.3. On comparing the ratios \frac{a_{1}}{a_{2}} , \frac{b_{1}}{b_{2}} and \frac{c_{1}}{c_{2}} , find out whether the following pair of linear equations are consistent, or inconsistent.
(i) 3 x + 2 y = 5; 2 x – 3 y = 7
Solution: The given pair of linear equation are:
3 x + 2 y – 5 = 0 …(i)
2 x – 3 y – 7 = 0 …(ii)
Comparing the eqn. (i) and (ii) with a_{1}x + b_{1}y + c_{1} = 0 and a_{2}x + b_{2}y + c_{2} = 0 respectively,
a_{1} = 3, b_{1} = 2, c_{1} = – 5
a_{2} = 2, b_{2} = – 3, c_{2} = – 7
Here,
\frac{a_{1}}{a_{2}} = \frac{3}{2}
\frac{b_{1}}{b_{2}} = \frac{2}{-3}
\frac{c_{1}}{c_{2}} = \frac{-5}{-7} = \frac{5}{7}
Clearly, \frac{3}{2} ≠ \frac{2}{-3} ≠ \frac{5}{7}
Hence, \frac{a_{1}}{a_{2}} ≠ \frac{b_{1}}{b_{2}} ≠ \frac{c_{1}}{c_{2}}
So, pair of linear equations are consistent.
(ii) 2 x – 3 y = 8; 4 x – 6 y = 9
Solution: The given pair of linear equation are :
2 x – 3 y – 8 = 0 …(i)
4 x – 6 y – 9 = 0 …(ii)
Comparing the eqn. (i) and (ii) with a_{1}x + b_{1}y + c_{1} = 0 and a_{2}x + b_{2}y + c_{2} = 0 respectively,
a_{1} = 2, b_{1} = – 3, c_{1} = – 8
a_{2} = 4, b_{2} = – 6, c_{2} = – 9
Here,
\frac{a_{1}}{a_{2}} = \frac{2}{4} = \frac{1}{2}
\frac{b_{1}}{b_{2}} = \frac{-3}{-6} = \frac{1}{2}
\frac{c_{1}}{c_{2}} = \frac{-8}{-9} = \frac{8}{9}
Clearly, \frac{1}{2} = \frac{1}{2} ≠ \frac{8}{9}
Hence, \frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} ≠ \frac{c_{1}}{c_{2}}
So, pair of linear equations are inconsistent.
(iii) \frac{3}{2}x + \frac{5}{3}y = 7; 9 x – 10 y = 14
Solution: The given pair of linear equation are :
\frac{3}{2}x + \frac{5}{3}y = 7
9 x + 10 y – 42 = 0 …(i)
9 x – 10 y – 14 = 0 …(ii)
Comparing the eqn. (i) and (ii) with a_{1}x + b_{1}y + c_{1} = 0 and a_{2}x + b_{2}y + c_{2} = 0 respectively,
a_{1} = 9, b_{1} = 10, c_{1} = – 42
a_{2} = 9, b_{2} = – 10, c_{2} = – 14
Here,
\frac{a_{1}}{a_{2}} = \frac{9}{9} = \frac{1}{1}
\frac{b_{1}}{b_{2}} = \frac{10}{-10} = \frac{1}{-1}
\frac{c_{1}}{c_{2}} = \frac{-42}{-14} = \frac{3}{1}
Clearly, \frac{1}{1} ≠ \frac{1}{-1} ≠ \frac{3}{1}
Hence, \frac{a_{1}}{a_{2}} ≠ \frac{b_{1}}{b_{2}} ≠ \frac{c_{1}}{c_{2}}
So, pair of linear equations are consistent.
(iv) 5 x – 3 y = 11; –10 x + 6 y = –22
Solution: The given pair of linear equation are :
5 x – 3 y – 11 = 0 …(i)
–10 x + 6 y + 22 = 0 …(ii)
Comparing the eqn. (i) and (ii) with a_{1}x + b_{1}y + c_{1} = 0 and a_{2}x + b_{2}y + c_{2} = 0 respectively,
a_{1} = 5, b_{1} = – 3, c_{1} = – 11
a_{2} = – 10, b_{2} = 6, c_{2} = 22
Here,
\frac{a_{1}}{a_{2}} = \frac{5}{-10} = \frac{1}{-2}
\frac{b_{1}}{b_{2}} = \frac{-3}{6} = \frac{-1}{2}
\frac{c_{1}}{c_{2}} = \frac{-11}{22} = \frac{-1}{2}
Clearly, \frac{-1}{2} = \frac{-1}{2} = \frac{-1}{2}
Hence, \frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} = \frac{c_{1}}{c_{2}}
So, pair of linear equations are consistent.
(v) \frac{4}{3}x + 2 y = 8; 2 x + 3 y = 12
Solution: The given pair of linear equation are :
\frac{4}{3}x + 2 y = 8
4 x + 6 y – 24 = 0 …(i)
2 x + 3 y – 12 = 0 …(ii)
Comparing the eqn. (i) and (ii) with a_{1}x + b_{1}y + c_{1} = 0 and a_{2}x + b_{2}y + c_{2} = 0 respectively,
a_{1} = 4, b_{1} = 6, c_{1} = – 24
a_{2} = 2, b_{2} = 3, c_{2} = – 12
Here,
\frac{a_{1}}{a_{2}} = \frac{4}{2} = \frac{2}{1}
\frac{b_{1}}{b_{2}} = \frac{6}{3} = \frac{2}{1}
\frac{c_{1}}{c_{2}} = \frac{-24}{-12} = \frac{2}{1}
Clearly, \frac{1}{1} = \frac{1}{-1} = \frac{3}{1}
Hence, \frac{a_{1}}{a_{2}} = \frac{b_{1}}{b_{2}} = \frac{c_{1}}{c_{2}}
So, pair of linear equations are consistent.
Exercise 2.2
Question.1. Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients :
(i) x^{2}-2x-8
Solution: Let p(x) = x^{2}-2x-8
= x^{2}-4x+2x-8
= x(x-4)+2(x-4)
= (x – 4)(x + 2)
For finding the zeroes
Put, p(x) = 0
= (x – 4)(x + 2) = 0
x = 4, – 2
Verification: Now, sum of zeroes = 4 + (– 2)
= {\frac{2}{1}}
= {\frac{-(Coefficient of x)}{(Coefficient of x^{2})}}
Product of zeroes = 4 \times (– 2)
= {\frac{-8}{1}}
= {\frac{Constant term}{Coefficient of x^{2}}}
Hence, relationship between the zeroes and the coefficients is true.
(ii) 4s^{2}-4s+1
Solution: Let p(s) = 4s^{2}-4s+1
= 4s^{2}-2s-2s+1
= 2s(2s-1)-1(2s-1)
= (2s – 1) (2s – 1)
= (2s-1)^{2}
For finding the zeroes, put p(s) = 0.
2s – 1 = 0
s = \frac{1}{2}
Hence, zeroes of p(s) are \frac{1}{2} and 12 \frac{1}{2} .
Verification: Now, sum of zeroes = \frac{1}{2} + \frac{1}{2}
= 1 = \frac{4}{4} = {\frac{-(Coefficient of s)}{(Coefficient of s^{2})}}
Product of zeroes = \frac{1}{2} \times \frac{1}{2}
= \frac{1}{4}
= {\frac{Constant term}{Coefficient of s^{2}}}
Hence, relationship between the zeroes and the coefficients is true.
(iii) 6x^{2}-3-7x
Solution: Let p(x) = 6x^{2}-3-7x = 6x^{2}-7x-3
= 6x^{2}-9x+2x-3
= 3x(2x-3)+1(2x-3)
= (2x – 3) (3x + 1)
For finding the zeroes put p(x) = 0
(2x – 3) (3x + 1) = 0
x = {\frac{3}{2}}, {\frac{-1}{3}}
Hence, zeroes of the polynomial are {\frac{3}{2}} and {\frac{-1}{3}}.
Verification: Now sum of zeroes = {\frac{3}{2}} + {\frac{-1}{3}}
= {\frac{9-2}{6}}
= {\frac{7}{6}}
= {\frac{-(Coefficient of x)}{(Coefficient of x^{2})}}
Product of zeroes = {\frac{3}{2}} \times {\frac{(-1)}{3}}
= {\frac{-3}{6}}
= {\frac{Constant term}{Coefficient of x^{2}}}
(iv) 4u^{2}+8u
Solution: Let p(u) = 4u^{2}+8u
= 4u (u + 2)
For finding the zeroes put p(u) = 0,
4u (u + 2) = 0
u = 0, – 2
Hence, zeroes are 0 and – 2.
Verification: Now sum of zeroes = 0 + (– 2)
= {\frac{-2}{1}} \times {\frac{4}{4}}
= {\frac{-8}{4}}
= {\frac{-(Coefficient of u)}{(Coefficient of u^{2})}}
Product of zeroes = 0 \times (– 2)
= {\frac{0}{1}} \times {\frac{4}{4}}
= {\frac{0}{4}}
= {\frac{Constant term}{Coefficient of u^{2}}}
Hence, relationship between the zeroes and the coefficients is true.
(v) t^{2}-15
Solution: Let p(t) = t^{2}-15 .
= t^{2}-(\sqrt{15})^{2}
= (t-\sqrt{15})(t+\sqrt{15}) [∵ a^{2}-b^{2} = (a + b) (a – b)]
For finding the zeroes put p(t) = 0,
(t-\sqrt{15})(t+\sqrt{15}) = 0
t = -\sqrt{15}) , \sqrt{15}
Verification: Sum of the zeroes = -\sqrt{15}) + \sqrt{15}
= {\frac{0}{1}}
= = {\frac{-(Coefficient of t)}{(Coefficient of t^{2})}}
Product of zeroes = -\sqrt{15}) \times \sqrt{15}
= {-\frac{15}{1}}
= {\frac{Constant term}{Coefficient of t^{2}}}
Hence, relationship between the zeroes and the coefficients is true.
(vi) 3x^{2}-x-4
Solution: Let p(x) = 3x^{2}-x-4
= 3x^{2}-4x+3x-4
= x(3x – 4) + 1 (3x – 4)
= (x + 1) (3x – 4)
For finding the zeroes put p(x) = 0,
(x + 1) (3x – 4) = 0
x = -1, {\frac{4}{3}}
Verification: Sum of zeroes = -1 + {\frac{4}{3}}
= {\frac{1}{3}}
= = {\frac{-(Coefficient of x)}{(Coefficient of x^{2})}}
Product of zeroes = -1 \times {\frac{4}{3}}
= {\frac{-4}{3}}
= {\frac{Constant term}{Coefficient of x^{2}}}
Hence, relationship between the zeroes and the coefficients is true.
Question.2. Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively.
(i) {\frac{1}{4}}, – 1
Solution: Let quadratic polynomial is p(x) whose zeroes are α and β.
Given that : α + β = 14 and αβ = – 1
So, required polynomial = k[x^{2} – (α + β)x + αβ]
= k\left[x^{2}-\frac{1}{4}x-1\right]
If k = 4, then 4x^{2}-x-4 .
(ii) \sqrt{2}, {\frac{1}{3}}
Solution: Let quadratic polynomial is ax^{2}+bx+c whose zeroes are α and β.
Given that: α + β = \sqrt{2} and αβ = 13
So, required polynomial = k[x^{2} – (α + β)x + αβ]
= k\left[x^{2}-\sqrt{2}x+{\frac{1}{3}}\right]
If k = 3, then 3x^{2}-3 \sqrt{2}x+1 .
(iii) 0, \sqrt{5}
Solution: Let quadratic polynomial is ax^{2}+bx+c whose zeroes are α and β.
Given that: α + β = 0 and αβ = \sqrt{5}
Hence, required polynomial = k[x^{2} – (α + β)x + αβ]
= k\left[x^{2}-0.x+ \sqrt{5} \right]
= k\left[x^{2}+ \sqrt{5} \right]
If k = 1, then x^{2}+ \sqrt{5} .
(iv) 1, 1
Solution: Let quadratic polynomial is ax^{2}+bx+c whose zeroes are α and β.
Given that : α + β = 1 and αβ = 1
Hence, required polynomial = k[x^{2} – (α + β)x + αβ]
= k\left[x^{2}-x+1 \right]
If k = 1, then x^{2}-x+1 .
(v) {\frac{-1}{4}}, {\frac{1}{4}}
Solution: Let quadratic polynomial is ax^{2}+bx+c whose zeroes are α and β.
Given that: α + β = -{\frac{1}{3}} and αβ = {\frac{1}{3}}
So, required polynomial = k[x^{2} – (α + β)x + αβ]
= k\left[x^{2}+\frac{1}{4}x+\frac{1}{4} \right]
If k = 4, then 4x^{2}+x+1 .
(vi) 4, 1
Solution: Let quadratic polynomial is ax^{2}+bx+c whose zeroes are α and β.
Given that: α + β = 4 and αβ = 1
Hence, required polynomial = k[x^{2} – (α + β)x + αβ]
= k\left[x^{2}-4x+1 \right].